Giải SGK Toán 8 trang 71, 72 Chân trời sáng tạo tập 1
Giải bài 1, 2 trang 71, bài 3. 4. 5. 6. 7 trang 72 SGK Toán lớp 8 chân trời sáng tạo tập 1. Bài 2. Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang.
Bài 1 trang 71 SGK Toán 8 tập 1 - Chân trời sáng tạo
Tìm \(x\) và \(y\) ở các hình sau.
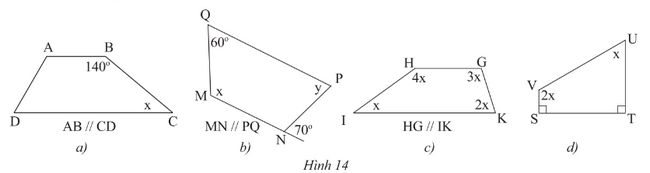
Phương pháp:
Sử dụng tính chất của hai đường thẳng song song, định lý tổng bốn góc trong tứ gíac
Lời giải:


Bài 2 trang 71 SGK Toán 8 tập 1 - Chân trời sáng tạo
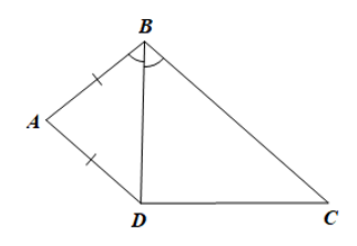
Cho tứ giác \(ABCD\) có \(AB = AD\), \(BD\) là tia phân giác của góc \(B\). Chứng minh rằng \(ABCD\) là hình thang.
Phương pháp:
Chứng minh \(AD\) // \(BC\)
Lời giải:

Bài 3 trang 72 SGK Toán 8 tập 1 - Chân trời sáng tạo
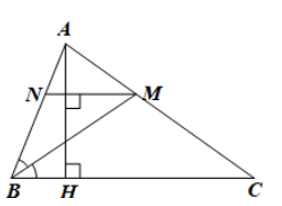
Cho tam giác nhọn \(ABC\) có \(AH\) là đường cao. Tia phân giác của góc \(B\) cắt \(AC\) tại \(M\). Từ \(M\) kẻ đường thẳng vuông góc với \(AH\) và cắt \(AB\) tại \(N\). Chứng minh rằng:
a) Tứ giác \(BCMN\) là hình thang
b) \(BN = MN\)
Phương pháp:
a) Chứng minh \(NM\) // \(BC\) rồi chỉ ra \(BNMC\) là hình thang
b) Chứng minh \(\Delta BNM\) cân tại \(N\)
Lời giải:

Bài 4 trang 72 SGK Toán 8 tập 1 - Chân trời sáng tạo
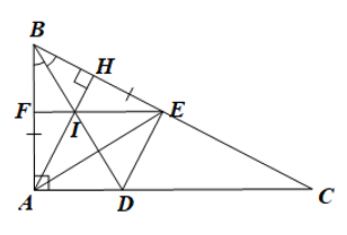
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của góc \(B\) cắt \(AC\) tại \(D\). Trên \(BC\) lấy điểm\(E\) sao cho \(BE = BA\).
a) Chứng minh rằng \(\Delta ABD = \Delta EBD\)
b) Kẻ đường cao \(AH\) của tam giác \(ABC\). Chứng minh rằng tứ giác \(ADEH\) là hình thang vuông.
c) Gọi \(I\) là giao điểm của \(AH\) với \(BD\), đường thẳng \(EI\) cắt \(AB\) tại \(F\). Chứng minh rằng tứ giác \(ACEF\) là hình thang vuông.
Phương pháp:
a) Áp dụng trường hợp bằng nhau c-g-c
b) + c) Áp dụng dấu hiệu nhận biết của hình thang và định nghĩa hình thang vuông
Lời giải:


Bài 5 trang 72 SGK Toán 8 tập 1 - Chân trời sáng tạo
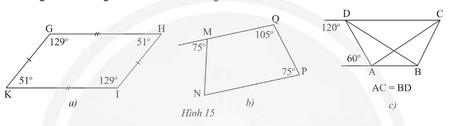
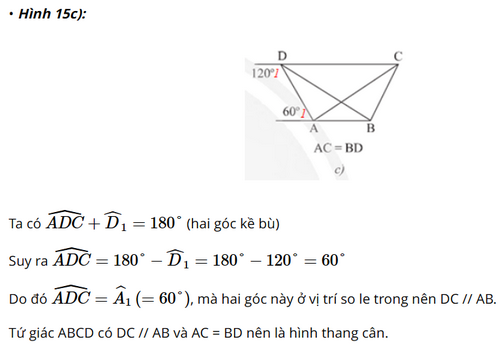
Tứ giác nào trong Hình 15 là hình thang cân?
Phương pháp:
Sử dụng dấu hiệu nhận biết hình thang cân
Lời giải:
• Hình 15a):
Ta thấy hai góc kề một đáy của tứ giác GHIK có số đo là 51° và 129° không bằng nhau.
Do đó tứ giác GHIK không phải là hình thang cân.

Bài 6 trang 72 SGK Toán 8 tập 1 - Chân trời sáng tạo
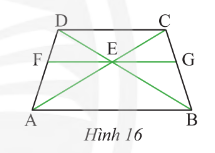
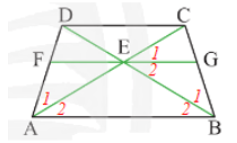
Cho hình thang cân \(ABCD\) có \(AB\) // \(CD\). Qua gia điểm \(E\) của \(AC\) và \(BD\), ta vẽ đường thẳng song song với \(AB\) và cắt \(AD\), \(BC\) lần lượt tại \(F\) và \(G\) (Hình 16). Chứng minh rằng \(EG\) là tia phân giác của góc \(CEB\).
Phương pháp:
Chứng minh \(\widehat {{\rm{CEG}}} = \widehat {{\rm{BEG}}}\)
Lời giải:

Bài 7 trang 72 SGK Toán 8 tập 1 - Chân trời sáng tạo
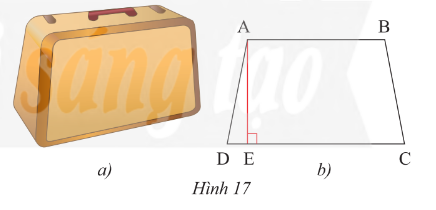
Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là \(60\)cm, cạnh bên là \(61\)cm và đáy lớn là \(92\)cm. Tính độ dài đáy nhỏ.
Phương pháp:
Tính \(DE\) (sử dụng định lý Pythagore)
Tính\(AB\)
Lời giải:
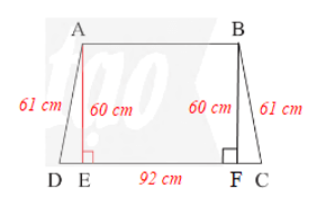
Áp dụng định lí Pythagore vào DADE vuông tại E, ta có:
AD2 = AE2 + DE2
Suy ra DE2 = AD2 – AE2 = 612 – 602 = 3 721 – 3 600 = 121 = 112
Do đó DE = 11 cm.
Kẻ BF ⊥ CD, khi đó BF là đường cao của hình thang cân ABCD nên BF = 60 cm.
Xét DADE và DBCF có:
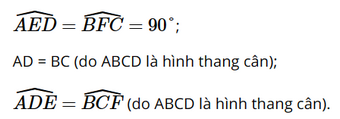
Do đó DADE = DBCF (cạnh huyền – góc nhọn)
Suy ra DE = CF = 11 cm (hai cạnh tương ứng).
Mà DE + EF + CF = DC
Nên EF = DC – DE – CF = 92 – 11 – 11 = 70 cm.
Tương tự Vận dụng 4, trang 71, Sách giáo khoa Toán 8, tập một, ta dễ dàng chứng minh được AB = EF = 70 cm.
Vậy độ dài đáy nhỏ của hình thang cân là 70 cm.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 trang 95, 96 SGK Toán 8 Chân trời sáng tạo tập 2 (05/12)
- Giải bài 1, 2, 3, 4 trang 94 SGK Toán 8 Chân trời sáng tạo tập 2 (05/12)
- Giải bài 1, 2, 3, 4, 5 trang 90, 91 SGK Toán 8 Chân trời sáng tạo tập 2 (05/12)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,17 trang 84, 85, 86 SGK Toán 8 Chân trời sáng tạo tập 2 (05/12)
- Giải bài 1, 2, 3, 4 trang 82, 83 SGK Toán 8 Chân trời sáng tạo tập 2 (05/12)
- Bài tập cuối chương 9
- Bài 2. Xác suất lí thuyết và xác suất thực nghiệm
- Bài 1. Mô tả xác suất bằng tỉ số
- CHƯƠNG IX. MỘT SỐ YẾU TỐ XÁC SUẤT
- Bài tập cuối chương 8
- Bài 4. Hai hình đồng dạng
- Bài 3. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 2. Các trường hợp đồng dạng của hai tam giác
- Bài 1. Hai tam giác đồng dạng
- CHƯƠNG VIII. HÌNH ĐỒNG DẠNG
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
