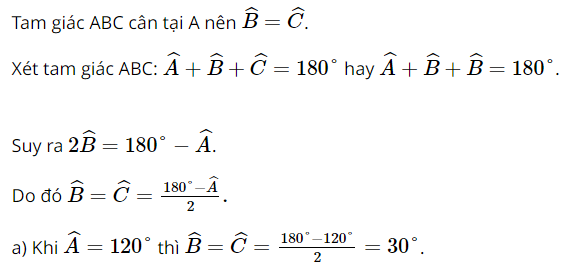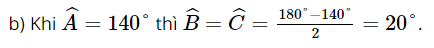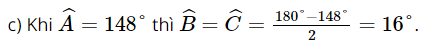Giải Toán 7 trang 96 Cánh Diều tập 2

Bài 1 trang 96 SGK Toán 7 tập 2 - Cánh Diều

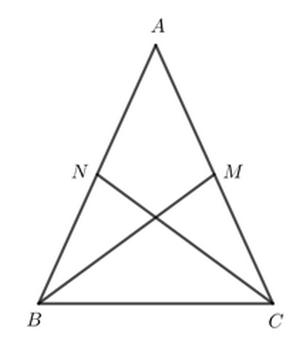
Cho tam giác ABC cân tại A có M là trung điểm cạnh AC và N là trung điểm cạnh AB. Chứng minh \(BM = CN\)

Phương pháp:

Chứng minh BM = CN bằng cách chứng minh tam giác AMB bằng tam giác ANC .

Lời giải:

Tam giác ABC cân tại A nên AB = AC.

AB = AC (chứng minh trên).

Suy ra ∆AMB = ∆ANC (c - g - c).

Do đó BM = CN (2 cạnh tương ứng).

Bài 2 trang 96 SGK Toán 7 tập 2 - Cánh Diều

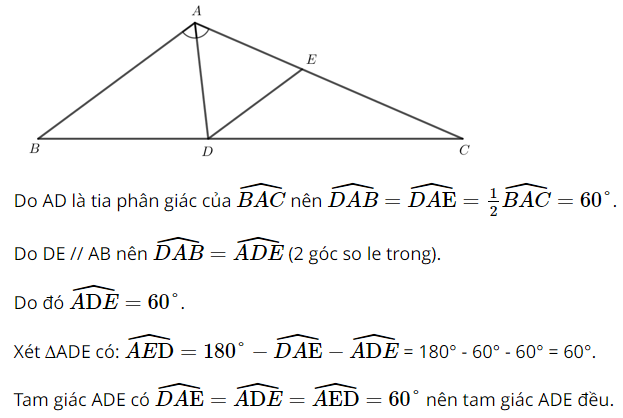
Cho tam giác ABC có \(\widehat A = 120^\circ \). Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.

Phương pháp:

Chứng minh tam giác ADE đều ta chứng minh ba góc trong tam giác ADE đều bằng 60°.

Lời giải:

Bài 3 trang 96 SGK Toán 7 tập 2 - Cánh Diều

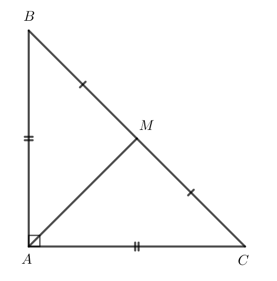
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.

Phương pháp:

Ta chứng minh tam giác MAB vuông cân bằng cách chứng minh trong tam giác có một góc vuông tại một đỉnh và có cặp cạnh bằng nhau xuất phát từ đỉnh đó.

Lời giải:

Xét ∆AMB và ∆AMC có:

AM chung.

BM = CM (M là trung điểm của BC).

AB = AC (tam giác ABC cân tại A).

Suy ra ∆AMB = ∆AMC (c - c - c).

Suy ra AM ⊥ BM hay tam giác MAB vuông tại M (2).

Từ (1) và (2) suy ra tam giác MAB vuông cân tại M.

Vậy tam giác MAB vuông cân tại M.

Bài 4 trang 96 SGK Toán 7 tập 2 - Cánh Diều

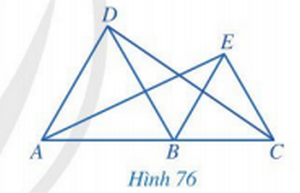
Trong Hình 76, cho biết các tam giác ABD và BCE là tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

a) AD // BE và BD // CE;

b) \(\widehat {ABE} = \widehat {DBC} = 120^\circ \);

c) AE = CD.

Phương pháp:

a) Ta chứng minh AD // BE và BD // CE dựa vào các cặp góc bằng nhau ở vị trí đồng vị.

b) Chứng minh \(\widehat {ABE} = \widehat {DBC} = 120^\circ \)dựa vào số đo góc của ba điểm thẳng hàng là 180°.

c) Chứng minh AE = CD bằng cách chứng minh tam giác ABE bằng tam giác DBC

Lời giải:

Bài 5 trang 96 SGK Toán 7 tập 2 - Cánh Diều

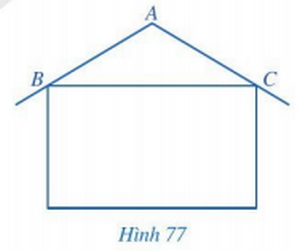
Trong thiết kế của một ngôi nhà, độ nghiêng của mái nhà so với phương nằm ngang phải phù hợp với kết cấu của ngôi nhà và vật liệu làm mái nhà. Hình 77 mô tả mặt cắt đứng của ngôi nhà, trong đó độ nghiêng của mái nhà so với phương nằm ngang được biểu diễn bởi số đo góc ở đáy của tam giác ABC cân tại A.

Tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong mỗi trường hợp sau:

a) Góc ở đỉnh A là (khoảng) 120° đối với mái nhà lợp bằng ngói;

b) Góc ở đỉnh A là (khoảng) 140° đối với mái nhà lợp bằng fibro xi măng;

c) Góc ở đỉnh A là (khoảng) 148° đối với mái nhà lợp bằng tôn.

Phương pháp:

Dựa vào tổng ba góc trong một tam giác bằng 180° để tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang.

Lời giải:

Vậy khi góc ở đỉnh A khoảng 120° thì độ nghiêng của mái nhà so với mặt phẳng nằm ngang là khoảng 30°.

Vậy khi góc ở đỉnh A khoảng 140° thì độ nghiêng của mái nhà so với mặt phẳng nằm ngang là khoảng 20°.

Vậy khi góc ở đỉnh A khoảng 148° thì độ nghiêng của mái nhà so với mặt phẳng nằm ngang là khoảng 16°. 

Sachbaitap.com