Giải bài 1, 2, 3, 4, 5 trang 71, 72 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo
Giải bài tập bài 1. Hình có trục đối xứng - sách bài tập Toán 6 tập 2 sách chân trời sáng tạo trang 71: bài 1, 2, 3, 4, 5.
Bài 1 trang 71 - SBT Toán 6 tập 2 - Chân trời sáng tạo
Câu hỏi:
Vẽ trục đối xứng của mỗi hình sau:

Phương pháp:
Trục đối xứng là đường thẳng mà khi gấp hình theo đường đó ta được hai phần chồng khít lên nhau
Trả lời:
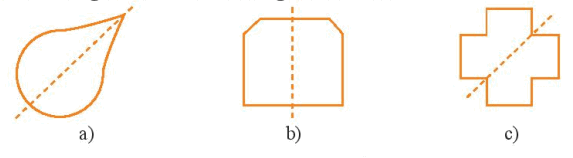
Các đường nét đứt là trục đối xứng của mỗi hình sau:
Bài 2 trang 71 - SBT Toán 6 tập 2 - Chân trời sáng tạo
Câu hỏi:
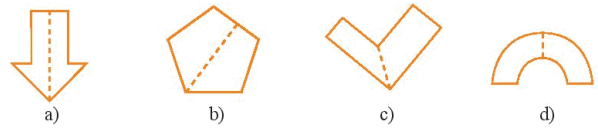
Hình nào sau đây có đường nét đứt là trục đối xứng
Phương pháp:
Quan sát 2 phần được chia bởi đường nét đứt, nếu chúng giống hệt nhau thì đường nét đứt là trục đối xứng của hình đó.
Trả lời:
Hình a), b), d) có đường nét đứt chia hình đó thành hai phần bằng nhau nên những hình này có trục đối xứng.
Hình c) có đường nét đứt chia hình đó thành hai phần không bằng nhau nên hình này không có trục đối xứng.
Vậy hình a), b), d) có đường nét đứt là trục đối xứng.
Bài 3 trang 71 - SBT Toán 6 tập 2 - Chân trời sáng tạo
Câu hỏi:
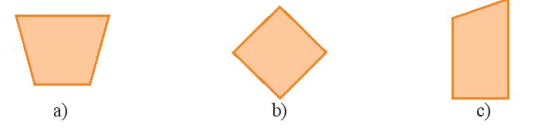
Mỗi hình sau đây có bao nhiêu trục đối xứng?
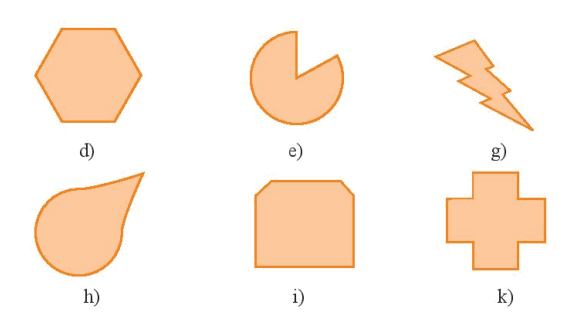
Phương pháp:
Số trục đối xứng là số đường thẳng chia hình đó thành hai phần bằng nhau (giống hệt nhau)
Trả lời:
|
a |
b |
c |
d |
e |
g |
h |
i |
k |
|
1 |
4 |
0 |
6 |
1 |
0 |
1 |
1 |
4 |
Bài 4 trang 72 - SBT Toán 6 tập 2 - Chân trời sáng tạo
Câu hỏi:
Hãy vẽ trục đối xứng của mỗi hình sau nếu có thể:
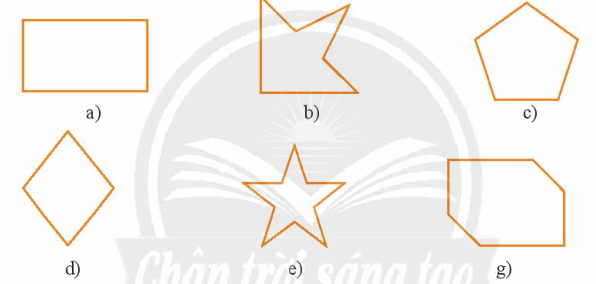
Phương pháp:
Trục đối xứng là đường thẳng mà khi gấp hình theo đường đó ta được hai phần chồng khít lên nhau
Trả lời:
Các hình a, b, c, d, e có đường nét liền màu đen là trục đối xứng của hình đó. Hình g không có trục đối xứng.
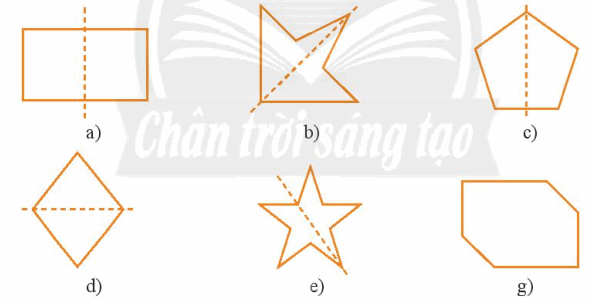
Bài 5 trang 72 - SBT Toán 6 tập 2 - Chân trời sáng tạo
Câu hỏi:
Vẽ thêm để các hình sau có trục đối xứng là đường nét đứt trên hình vẽ.
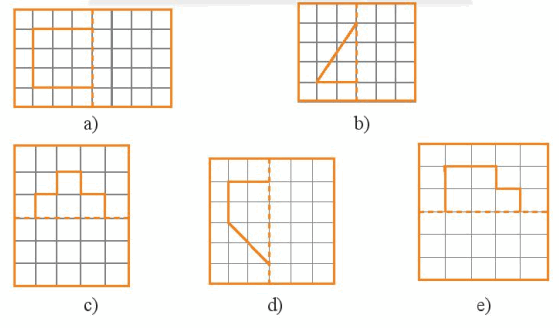
Trả lời:
Coi đường nét đứt như một cái gương, vẽ thêm sao cho khi gập hình theo đường nét đứt ta được hai phần giống hệt và chồng khít lên nhau.
Hình sau khi được vẽ thêm có đường nét đứt là trục đối xứng được biểu diễn như sau:
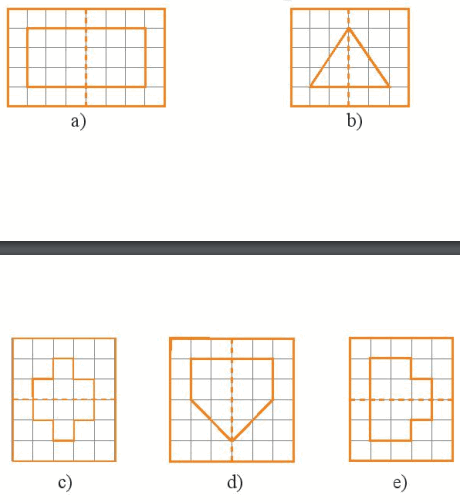
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 127, 128, 129 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo (01/03)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 123, 124, 125, 126 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo (01/03)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 119, 120 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo (01/03)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 102, 103, 104 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo (01/03)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 101, 102 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo (01/03)
- Bài tập cuối chương 9. MỘT SỐ YẾU TỐ THỐNG KÊ - CTST
- Bài 2. Xác suất thực nghiệm - CTST
- Bài 1. Phép thử nghiệm - Sự kiện - CTST
- CHƯƠNG 9. MỘT SỐ YẾU TỐ XÁC SUẤT - SBT CHÂN TRỜI SÁNG TẠO
- Bài tập cuối chương 8. HÌNH HỌC PHẲNG. CÁC HÌNH HỌC CƠ BẢN - CTST
- Bài 7. Số đo góc. Các góc đặc biệt - CTST
- Bài 6. Góc - CTST
- Bài 5. Trung điểm của đoạn thẳng - CTST
- Bài 4. Đoạn thẳng. Độ dài đoạn thẳng - CTST
- Bài 3. Hai đường thẳng cắt nhau, song song. Tia - CTST
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
