Bài 1, 2, 3, 4 trang 68, 69 SGK Toán 9 tập 1 - Một số hệ thức về cạnh và đường cao trong tam giác vuông

Bài 1 trang 68 SGK Toán lớp 9 tập 1

Câu hỏi:

Hãy tính \(x\) và \(y\) trong mỗi hình sau (hình \(4a,\ b)\):  

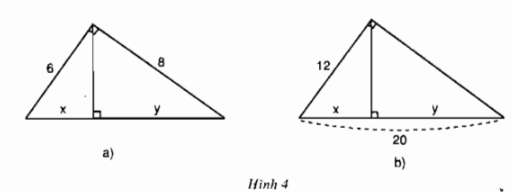
Lời giải: 

a) Đặt tên các đỉnh của tam giác như hình dưới:

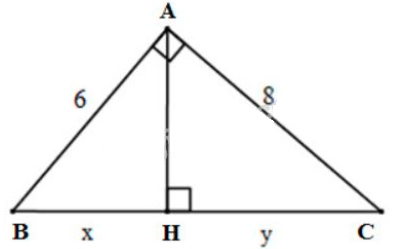
Áp dụng định lí Pytago vào \(\Delta{ABC}\) vuông tại \(A\), ta có:

\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)

 Áp dụng hệ thức lượng vào\(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có:

\(AB^2=BC.BH\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\)

Lại có \(HC=BC-BH=10-3,6=6,4\) 

Vậy \(x =BH= 3,6\);  \(y=HC = 6,4\).

b) Đặt tên các đỉnh của tam giác như hình dưới

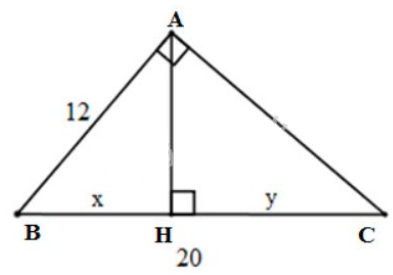
Áp dụng hệ thức lượng vào \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có:

\(AB^2=BH.BC  \Leftrightarrow 12^2=20.x \Rightarrow x=\dfrac{12^2}{20}=7,2\)

Lại có: \(HC=BC-BH=20-7,2=12,8\) 

Vậy \(x=BH = 7,2;\)  \(y=HC = 12,8\).

Bài 2 trang 68 SGK Toán lớp 9 tập 1

Câu hỏi:

Hãy tính \(x\) và \(y\) trong hình dưới đây:

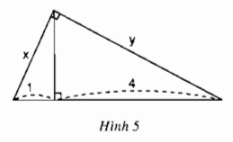
Phương pháp:

+) Sử dụng định lí Pytago trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\), khi đó: \(BC^2=AC^2+AB^2\). 

+) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền:

  \(b^2=a.b',\ c^2=a.c'\)

Lời giải:

Đặt tên các đỉnh như hình vẽ:

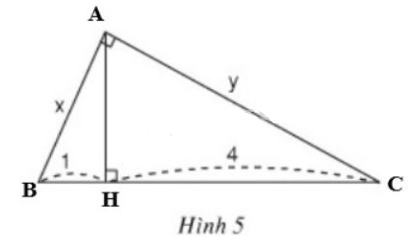
Ta có: \(BC=BH + HC=1+4=5\). 

Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), áp dụng hệ thức lượng trong tam giác vuông, ta có:

             \(AB^2=BH.BC \Leftrightarrow x^2=1.5\)  (với \(x > 0)\)

                                           \(\Leftrightarrow x^2=5\)

                                           \(\Leftrightarrow x=\sqrt 5\).

              \(AC^2=CH.BC \Leftrightarrow y^2=4.5\)  (với \(y> 0)\)

                                           \(\Leftrightarrow y^2=20\)

                                           \(\Leftrightarrow y=\sqrt{20}\)

                                           \(\Leftrightarrow y=2\sqrt{5}\).

Vậy \(x= \sqrt 5\), \(y=2\sqrt 5\). 

Bài 3 trang 69 SGK Toán lớp 9 tập 1

Câu hỏi:

Hãy tính \(x\) và \(y\) trong hình sau:

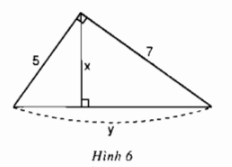
Lời giải:

Đặt tên các điểm như trong hình: 

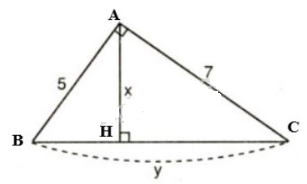
Xét \(\Delta{ABC}\) vuông tại \(A\). Theo định lí Pytago, ta có:

                       \(BC^2=AB^2+AC^2\)

                 \(\Leftrightarrow y^2=5^2+7^2\)

                \(\Leftrightarrow y^2=74\)

                \(\Leftrightarrow y=\sqrt{74}\)

Cách 1: \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), áp dụng công thức \(b.c=h.a\), ta được:

\(AB.AC=AH.BC \)

\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5.7}{\sqrt{74}}=\dfrac{35\sqrt{74}}{74}\).

Cách 2: Áp dụng hệ thức liên quan đến đường cao trong tam giác vuông, ta có:

                      \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

                  \(\Leftrightarrow \dfrac{1}{x^2}=\dfrac{1}{5^2}+\dfrac{1}{7^2}\)

                  \(\Leftrightarrow \dfrac{1}{x^2}=\dfrac{74}{1225}\)

                  \(\Leftrightarrow x=\sqrt{\dfrac{1225}{74}}\)

                  \( \Leftrightarrow x=\dfrac{35\sqrt{74}}{74}\)

Vậy \(\ x=\dfrac{35\sqrt{74}}{74}, \, y=\sqrt {74}\)

Bài 4 trang 69 SGK Toán lớp 9 tập 1

Câu hỏi:

Hãy tính \(x\) và \(y\) trong hình sau:

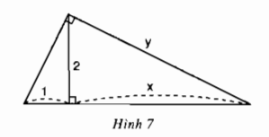
Phương pháp:

+) Sử dụng hệ thức liên quan đến đường cao và hình chiếu  \(h^2=b'.c'\). Biết \(h,\ c'\) tính được \(b'\).

+) Tính độ dài cạnh huyền: \(a=b'+c'\).

+) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền \(b^2=b'.a\). Biết \(a,\ b'\) tính được \(b\).

Lời giải:

Đặt tên các đỉnh của tam giác như hình bên dưới 

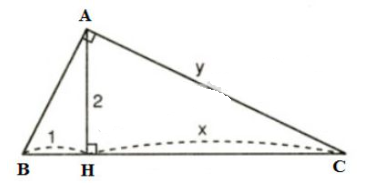
Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\).

Áp dụng hệ thức liên quan đến đường cao, ta có:

                     \(h^{2}=b'.c'\) 

             \(\Leftrightarrow AH^{2}=HB.HC\)

             \(\Leftrightarrow 2^2=1.x\)

             \(\Rightarrow x= 4.\)

Ta có: \(BC = BH+HC = 1+4=5 \)

Áp dụng hệ thức \(b^{2}=b'.a\), ta có:

                     \(AC^{2}=CH.BC\)

               \(   \Leftrightarrow y^{2}=5. 4\)

              \(\Leftrightarrow y^2=20\)

              \(\Leftrightarrow y =\sqrt{20}=2\sqrt{5}.\)

Vậy \(x=4,\ y=2\sqrt 5\).

Sachbaitap.com