Bài 2.6, 2.7, 2.8, 2.9 trang 23 SBT Toán 10 tập 1 Kết nối tri thức
Giải bài 4 trang 23 SBT Toán lớp 10 tập 1 Kết nối tri thức với cuộc sống: Hệ bất phương trình bậc nhất hai ẩn. Bài 2.6: Biểu diễn miền nghiệm của các hệ bất phương trình sau trên mặt phẳng tọa độ:
Bài 2.6 trang 23 SBT Toán lớp 10 tập 1 - Kết nối tri thức
Biểu diễn miền nghiệm của các hệ bất phương trình sau trên mặt phẳng tọa độ:
a) \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{y \ge 0}\\{x + y \le 4}\end{array}} \right.\)
b) \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{y > 0}\\{x - y - 4 < 0}\end{array}} \right.\)
c) \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{x \le 3}\\{x \ge - 1}\\{y \ge - 2}\end{array}} \right.\)
Lời giải:
a) \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{y \ge 0}\\{x + y \le 4}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(x \ge - 1\) là nửa mặt phẳng bờ \(d:x = - 1\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \(Ox\) chứa điểm \(\left( {0;4} \right).\)
Xác định miền nghiệm của bất phương trình\(x + y \le 4.\)
Vẽ đường thẳng \({d_2}:x + y = 4\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(x + y,\) ta được \(0 + 0 = 0 < 4.\)
Do đó, miền nghiệm của bất phương trình \({d_2}:x + y = 4\) là nửa mặt phẳng bờ \({d_2}\) và chứa điểm \(O\left( {0;0} \right).\)
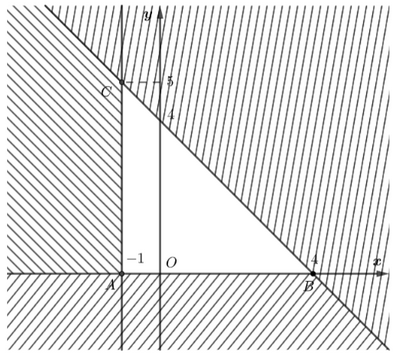
Vậy miền nghiệm của hệ bất phương trình trên là: \(\Delta ABC\) với \(A\left( { - 1;0} \right),\,\,B\left( {4;0} \right),\,\,C\left( { - 1;5} \right).\)
b) \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{y > 0}\\{x - y - 4 < 0}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(x > 0\) là nửa mặt phẳng bờ \(Oy\) chứa điểm \(\left( {1;0} \right)\) mà bỏ đi trục \(Oy.\)
Xác định miền nghiệm của bất phương trình \(y > 0\) là nửa mặt phẳng bờ \(Ox\) chứa điểm \(\left( {0;1} \right)\) mà bỏ đi trục \(Ox.\)
Xác định miền nghiệm của bất phương trình \(x - y - 4 < 0\).
Vẽ đường thẳng \({d_2}:x - y - 4 = 0\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn \(O\left( {0;0} \right)\) không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(x - y - 4,\) ta được \(0 - 0 - 4 = - 4 < 0.\)
Do đó, miền nghiệm của bất phương trình \(x - y - 4 < 0\) là nửa mặt phẳng bờ \({d_2}\) chứa điểm \(O\left( {0;0} \right)\) không kể \({d_2}\).
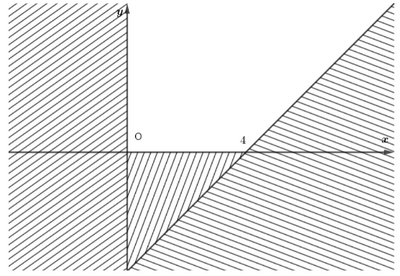
Miền nghiệm của hệ bất phương trình trên là phần không có gạch.
c) \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{x \le 3}\\{x \ge - 1}\\{y \ge - 2}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(y \le 3\) là nửa mặt phẳng bờ \(d:y = 3\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(x \le 3\) là nửa mặt phẳng bờ \({d_1}:x = 3\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(x \ge - 1\) là nửa mặt phẳng bờ \({d_3}:x = - 1\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(y \ge - 2\) là nửa mặt phẳng bờ \({d_4}:y = - 2\) chứa điểm \(O\left( {0;0} \right).\)
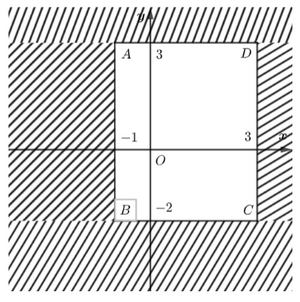
Miền nghiệm của hệ bất phương trình trên là: hình chữ nhật \(ABCD\) với \(A\left( { - 1;3} \right),\,\,B\left( { - 1; - 2} \right),\,\,C\left( {3; - 2} \right),\,\,D\left( {3;3} \right).\)
Bài 2.7 trang 23 SBT Toán lớp 10 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: \(F\left( {x;y} \right) = 2x + 3y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 6}\\{x \ge 0}\\{y \ge 0}\end{array}.} \right.\)
Lời giải:
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + y = 6 bằng cách vẽ đường thẳng đi qua hai điểm (6; 0) và (0; 6).
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x + y ta được 1 + 1 = 2 < 6.
Suy ra miền nghiệm của bất phương trình x + y ≤ 6 là nửa mặt phẳng bờ d1 có chứa điểm I(1; 1).
• Đường thẳng d2: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1) ∉d2 và thay vào biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d2 có chứa điểm I(1; 1).
• Đường thẳng d3: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1)∉ d3 và thay vào biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d3 có chứa điểm I(1; 1).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
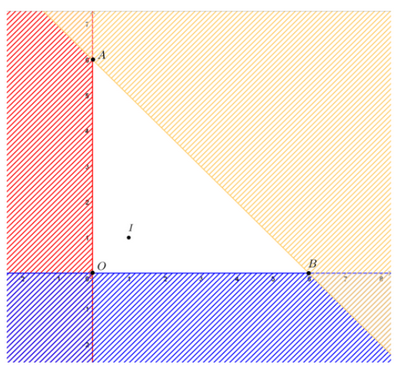
Ta thấy miền nghiệm của hệ bất phương trình đã cho là miền tam giác AOB với A(6; 0), O(0; 0) và B(0; 6).
F(6; 0) = 2 . 6 + 3. 0 = 12;
F(0; 0) = 2 . 0 + 3 . 0 = 0;
F(0; 6) = 2 . 0 + 3 . 6 = 18.
Do đó giá trị lớn nhất của F(x; y) = 18 khi x = 0 và y = 6; giá trị nhỏ nhất của F(x; y) = 0 khi x = 0 và y = 0.
Bài 2.8 trang 23 SBT Toán lớp 10 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: \(F\left( {x;y} \right) = 4x - 3y\) trên miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \ge - 4}\\{x + y \le 5}\\{x - y \le 5}\\{x - y \ge - 4}\end{array}.} \right.\)
Lời giải:
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + y = -4 bằng cách vẽ đường thẳng đi qua hai điểm (0; -4) và (-4; 0).
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x + y ta được 1 + 1 = 2 > -4.
Suy ra miền nghiệm của bất phương trình x + y ≥ -4 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Vẽ đường thẳng d2: x + y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; 5) và (5; 0).
Chọn điểm I(1; 1) ∉ d2 và thay vào biểu thức x + y ta được 1 + 1 = 2 < 5.
Suy ra miền nghiệm của bất phương trình x + y ≤ 5 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1).
• Vẽ đường thẳng d3: x - y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; -5) và (5; 0).
Chọn điểm I(1; 1) ∉ d3 và thay vào biểu thức x + y ta được 1 - 1 = 0 < 5.
Suy ra miền nghiệm của bất phương trình x - y ≤ 5 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1).
• Vẽ đường thẳng d4: x - y = -4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (-4; 0).
Chọn điểm I(1; 1) ∉ d4 và thay vào biểu thức x - y ta được 1 - 1 = 0 > -4.
Suy ra miền nghiệm của bất phương trình x - y ≥ -4 là nửa mặt phẳng bờ d4 chứa điểm I(1; 1).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
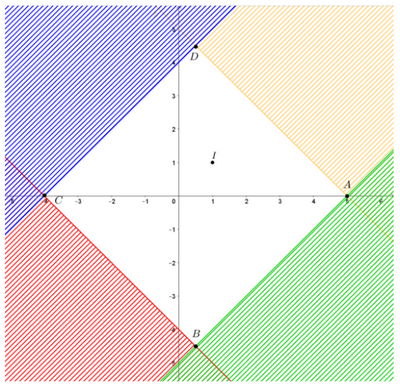
Miền nghiệm của hệ bất phương trình trên là hình vuông ABCD với A(5; 0), B(0,5; -4,5), C(-4; 0) và D(0,5; 4,5).
F(5; 0) = 4 . 5 - 3 . 0 = 20;
F(0,5; -4,5) = 4 . 0,5 - 3. (-4,5) = 15,5;
F(-4; 0) = 4 . (-4) - 3 . 0 = -16;
F(0,5; 4,5) = 4 . 0,5 - 3 . 4,5 = -11,5.
Vậy giá trị lớn nhất của F(x; y) = 20 khi x = 5 và y = 0 và giá trị nhỏ nhất của biểu thức F(x; y) = -16 khi x = -4 và y = 0.
Bài 2.9 trang 23 SBT Toán lớp 10 tập 1 - Kết nối tri thức
Trong một cuộc thi pha chế, mỗi đợi chơi được sử dụng tối đa 12g hương liệu, 9 lít nước và 315g đường để pha chế hai loại nước A và B. Để pha chết 1 lít nước A cần 45g đường, 1 lít nước và 0,5g hương liệu; để pha chế 1 lít nước B cần 15g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất?
Lời giải:
- Gọi \(x\) và \(y\) lần lượt là số lít nước loại A và B cần pha chế.
Điều kiện: \(x \ge 0,\,\,y \ge 0.\)
Số hương liệu cần dùng để pha chế hai loại lít nước A và B là: \(0,5x + 2y \le 12.\)
Số lít nước cần dùng để pha chế hai loại nước A và B là: \(x + y \le 9.\)
Số g đường cần dùng để pha chế hai loại lít nước A và B là: \(45x + 15y \le 315.\)
Từ đó, ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,5x + 2y \le 12}\\{x + y \le 9}\\{45x + 15y \le 315}\end{array}.} \right.\)
Số điểm thưởng của đội chơi nhận được là: \(F\left( {x;y} \right) = 60x + 80y \to \max \)
- Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,5x + 2y \le 12}\\{x + y \le 9}\\{45x + 15y \le 315}\end{array}} \right.\)trên cùng mặt phẳng tọa độ \(Oxy.\)
Xác định miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ \(d:x = 0\) chứa điểm \(\left( {1;0} \right).\)
Xác định miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \({d_1}:y = 0\) chứa điểm \(\left( {0;1} \right).\)
Xác định miền nghiệm của bất phương trình \(0.5x + 2y \le 12\). Vẽ đường thẳng \({d_2}:0.5x + 2y = 12\) trên mặt phẳng tọa độ \(Oxy.\) Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(0,5x + 2y,\) ta được: \(0,5.0 + 2.0 = 0 < 12\) nên miền nghiệm của bất phương trình \(0.5x + 2y \le 12\) là nửa mặt phẳng bờ \({d_2}\) chứa điểm \(O\left( {0;0} \right)\).
Xác định miền nghiệm của bất phương trình \(x + y \le 9\). Vẽ đường thẳng \({d_3}:x + y = 9\) trên mặt phẳng tọa độ \(Oxy.\) Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_3}\) và thay vào biểu thức \(x + y,\) ta được: \(0 + 0 = 0 < 9\) nên miền nghiệm của bất phương trình \(x + y = 9\) là nửa mặt phẳng bờ \({d_3}\) chứa điểm \(O\left( {0;0} \right)\).
Xác định miền nghiệm của bất phương trình \(45x + 15y \le 315\). Vẽ đường thẳng \({d_4}:45x + 15y = 315\) trên mặt phẳng tọa độ \(Oxy.\) Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_4}\) và thay vào biểu thức \(45x + 15y,\) ta được: \(45.0 + 15.0 = 0 < 315\) nên miền nghiệm của bất phương trình \(45x + 15y \le 315\) là nửa mặt phẳng bờ \({d_4}\) chứa điểm \(O\left( {0;0} \right)\).
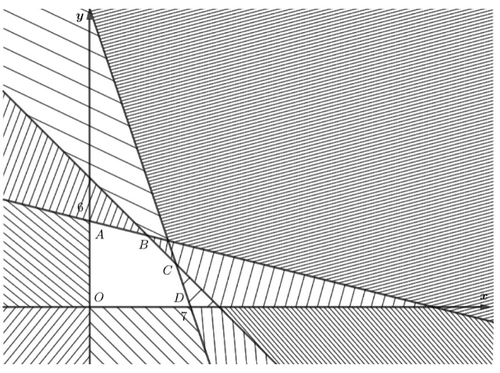
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,5x + 2y \le 12}\\{x + y \le 9}\\{45x + 15y \le 315}\end{array}} \right.\)là ngũ giác \(OABCD\) với \(A\left( {0;6} \right),\,\,B\left( {4;5} \right),\,\,C\left( {6;3} \right),\,\,D\left( {7;0} \right)\)
Ta có: \(F\left( {0;6} \right) = 60.0 + 80.6 = 480,\)
\(F\left( {4;5} \right) = 60.4 + 80.5 = 640,\)
\(F\left( {0;0} \right) = 60.0 + 80.0 = 0,\)
\(F\left( {6;3} \right) = 60.6 + 80.3 = 600,\)
\(F\left( {7;0} \right) = 60.7 + 80.0 = 420.\)
\( \Rightarrow \) giá trị lớn nhất là \(F\left( {4;5} \right) = 640.\)
Vậy vần pha chế 4 lít nước loại A và 5 lít nước loại B thì số điểm thưởng nhận được là lớn nhất.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SBT Toán 10 trang 70, 71, 72, 73 Kết nối tri thức tập 2 (16/11)
- Giải SBT Toán 10 trang 67, 68, 69 Kết nối tri thức tập 2 (27/02)
- Giải SBT Toán 10 trang 66 Kết nối tri thức tập 2 (27/02)
- Giải SBT Toán 10 trang 63 Kết nối tri thức tập 2 (27/02)
- Giải SBT Toán 10 trang 58, 59, 60 Kết nối tri thức tập 2 (27/02)
- Bài tập cuối chương 9
- Bài 27. Thực hành tính xác suất theo định nghĩa cổ điển
- Bài 26. Biến cố và định nghĩa cổ điển của xác suất
- CHƯƠNG 9. TÍNH XÁC SUẤT THEO ĐỊNH NGHĨA CỔ ĐIỂN
- Bài tập cuối chương 8
- Bài 25. Nhị thức Newton
- Bài 24. Hoán vị, chỉnh hợp và tổ hợp
- Bài 23. Quy tắc đếm
- CHƯƠNG 8. ĐẠI SỐ TỔ HỢP
- Bài tập cuối chương 7
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
