Bài 2.8 trang 103 Sách bài tập (SBT) Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) \(y = {x^{ - 3}}\)                            

b) \(y = {x^{ - {1 \over 2}}}\)                                    

c) \(y = {x^{{\pi  \over 4}}}\)

Hướng dẫn làm bài:

a) Tập xác định:  R\{0}

Hàm số đã cho là hàm số lẻ.

\(y' =  - 3{x^{ - 4}} =  - {3 \over {{x^4}}}\)                        

Ta có: \(y' < 0,\forall x \in R\backslash {\rm{\{ }}0\}\) nên hàm số luôn nghịch biến trên các khoảng xác định.

         \(\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  + \infty } y = 0,\mathop {\lim }\limits_{x \to {0^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to {0^ - }} y =  - \infty \)       

Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.

Bảng biến thiên:

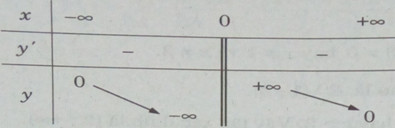
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.

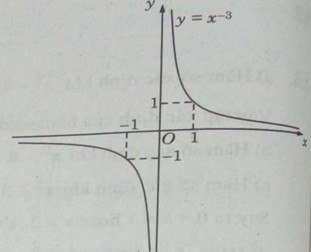
b) Tập xác định: \(D = (0; + \infty )\)

    \(y' =  - {1 \over 2}{x^{ - {3 \over 2}}}\)             

Vì  nên hàm số nghịch biến.

  \(\mathop {\lim }\limits_{x \to {0^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to  + \infty } y = 0\)                       

Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.

Bảng biến thiên:

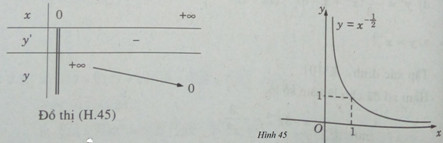
c) Tập xác định: \(D = (0; + \infty )\)

\(y' > 0,\forall x \in D\)                     

Vì \(y' > 0,\forall x \in D\) nên hàm số nghịch biến.

           \(\mathop {\lim }\limits_{x \to {0^ + }} y = 0,\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty \)            

Đồ thị không có tiệm cận.

Bảng biến thiên

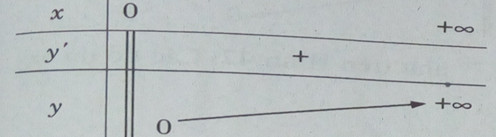
Đồ thị

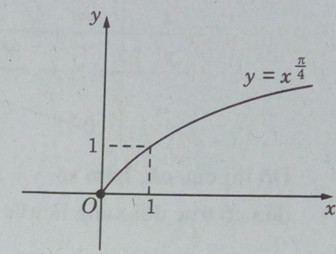
Sachbaitap.com