Bài 3.5 trang 35 Sách bài tập Vật lí 10 Nâng cao

Một vật nhỏ S khối lượng m được treo ở đầu một sợi chỉ mảnh. Vật S bị hút bởi một thanh thủy tinh hữu co nhiễm điện. Lực hút của thanh thủy tinh có phương nằm ngang. Vật S nằm cân bằng khi sợi chỉ làm một góc \(\alpha \) với phương thẳng đứng.

a) Lập bảng liệt kê với các lực đặt lên vật S.

b) Xác định góc \(\alpha \) theo các lực.

c) Tính lực căng của sợi dây.

Cho biết : m = 0,5g ; F = 3.10^-3 N; lấy g = 10g/s².

Giải:

a) Liệt kê các lực đặt lên vật :

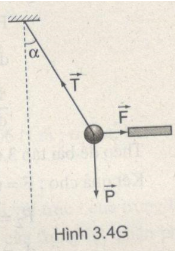
- Trọng lực \(\overrightarrow P \) đặt ở trọng tâm, hướng thẳng đứng xuống dưới ;

- Lực căng \(\overrightarrow T \) có phương của sợi dây, hướng lên phía trên ;

- Lực điện \(\overrightarrow F \) có phương nằm ngang, kéo vật làm dây lệch khỏi phương thẳng đứng ( xem Hình 3.4G).

b) Do vật nằm cân bằng, ta có :

\(\overrightarrow P  + \overrightarrow T  + \overrightarrow F  = \overrightarrow 0 \)          (1)

Chọn một hệ tọa độ xOy, có gốc trùng với vật, trục Ox nằm ngang hướng theo chiều lực \(\overrightarrow F \), trục Oy thẳng đứng lên trên. Phương trình vec tơ (1) có hai thành phần là :

- Trên trục Ox : \(0 + ( - T.\sin \alpha ) + F = 0\)   (2)

- Trên trục Oy : \( - P + T.\cos \alpha  + 0 = 0\)      (3)

Từ hai phương trình (2) và (3), ta suy ra :

\(\tan \alpha  = {F \over P}\)

Thay các giá trị P và F vào công thức trên, ta được :

\(\tan \alpha  = {{{{3.10}^{ - 3}}} \over {{{5.10}^{ - 3}}}} = 0,6,\) hay \(\alpha  \approx {31^0}\)

c) Lực căng của sợi dây :

\(T = {F \over {\sin \alpha }} = {{{{3.10}^{ - 3}}} \over {\sin {{31}^0}}} = 5,{8.10^{ - 3}}N\)

Sachbaitap.com