Bài 43 trang 62 Sách bài tập Hình học lớp 12 Nâng cao

Đường cao của hình nón gấp hai lần bán kính đáy của nó. Tính tỉ số thể tích hình cầu ngoại tiếp và nội tiếp hình nón đó.

Giải

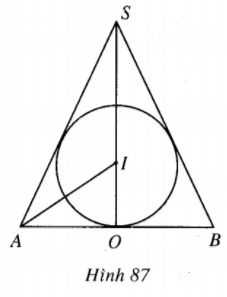
Xét mp(P) qua trục SO của hình nón thì (P) cắt hình nón theo tam giác cân SAB, (P) cắt mặt cầu ngoại tiếp và nội tiếp hình nón theo các đường tròn có bán kính lần lượt là R và r. Các đường tròn này ngoại tiếp và nội tiếp tam giác cân SAB.

Kí hiệu \({V_1},{V_2}\) là thể tích của các hình cầu đã nêu thì \({{{V_1}} \over {{V_2}}} = {\left( {{R \over r}} \right)^3}.\)

Đặt  \(\widehat {SAB}\) =\(\alpha \) và gọi I là tâm đường tròn nội tiếp \(\Delta SAB\) thì

\(2R = \) \(\frac{{AB}}{{\sin \widehat {{\rm{AS}}B}}}\)=\({{AB} \over {\sin 2\alpha }}\) và \(r = IO = {{AB} \over 2}\tan {\alpha  \over 2}.\)

Từ đó \({R \over r} = {1 \over {\sin 2\alpha \tan {\alpha  \over 2}}}.\)

Mặt khác \(\tan \alpha  = {{SO} \over {AO}} = 2,\) vậy

\(\eqalign{  & \sin 2\alpha  = {{2\tan \alpha } \over {1 + {{\tan }^2}\alpha }} = {4 \over 5};2 = \tan \alpha  = {{2\tan {\alpha  \over 2}} \over {1 - {{\tan }^2}{\alpha  \over 2}}}  \cr  &  \Rightarrow \tan {\alpha  \over 2} = {{\sqrt 5  - 1} \over 2} \cr} \)

( do \(\tan {\alpha  \over 2} > 0)\).

Như vậy \({R \over r} = {{5\left( {\sqrt 5  + 1} \right)} \over 8},\) tức là \({{{V_1}} \over {{V_2}}} = {{125{{\left( {\sqrt 5  + 1} \right)}^3}} \over {512}} \)

Sachbaitap.com