Bài 50, 51, 52, 53, 54, 55, 56 trang 58, 59 SGK Toán 8 tập 1 - luyện tập

Bài 50 trang 58 SGK Toán lớp 8 tập 1

Câu hỏi:

Thực hiện các phép tính:

 Phương pháp:

Áp dụng phân thức phép toán, trừ, nhân, chia.

Áp dụng tính chất phân phối giữa nhân viên và cộng đồng allow:

Lời giải:

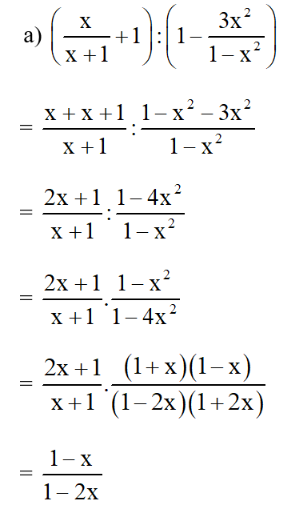
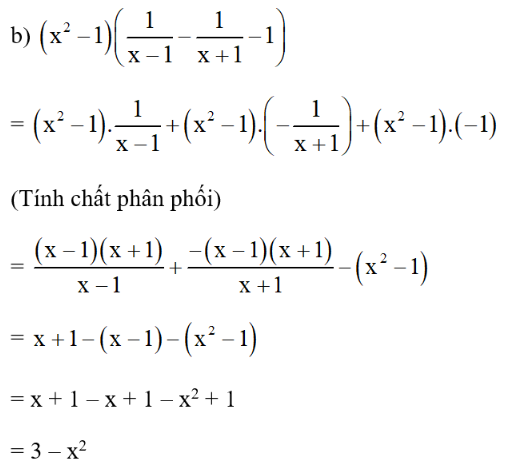
Bài 51 trang 58 SGK Toán lớp 8 tập 1

Câu hỏi:

Làm các phép tính sau:

a. \(\left( {\dfrac{{{x^2}}}{{{y^2}}} + \dfrac{y}{x}} \right):\left( {\dfrac{x}{{{y^2}}} - \dfrac{1}{y} + \dfrac{1}{x}} \right);\)

b. \(\left( {\dfrac{1}{{{x^2} + 4x + 4}} - \dfrac{1}{{{x^2} - 4x + 4}}} \right):\left( {\dfrac{1}{{x + 2}} + \dfrac{1}{{x - 2}}} \right)\)

Phương pháp:

Áp dụng các phép toán cộng, trừ, nhân, chia phân thức; thực hiện các phép tính trong ngoặc trước.

Lời giải:

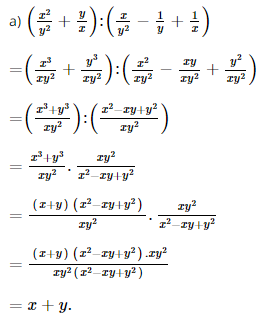
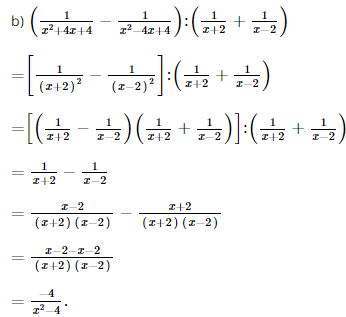
Bài 52 trang 58 SGK Toán lớp 8 tập 1

Câu hỏi:

Chứng tỏ rằng với \(x \ne 0\) và \(x \ne  \pm a\) (\(a\) là một số nguyên), giá trị của biểu thức

 \(\left( {a - \dfrac{{{x^2} + {a^2}}}{{x + a}}} \right).\left( {\dfrac{{2a}}{x} - \dfrac{{4a}}{{x - a}}} \right)\)  là một số chẵn.

Phương pháp:

- Tìm điều kiện xác định của phân thức là mẫu thức khác \(0\).

- Chứng tỏ biểu thức có giá trị dạng \(2k\) (\(k\) là một số nguyên)

Lời giải:

Bài 53 trang 58 SGK Toán lớp 8 tập 1

Câu hỏi:

a. Biến đổi mỗi biểu thức sau thành một phân thức đại số :

\(1 + \dfrac{1}{x}\);                 

\(1 + \dfrac{1}{{1 + \dfrac{1}{x}}}\) ;            

\(1 + \dfrac{1}{{1 + \dfrac{1}{{1 + \dfrac{1}{x}}}}}\)  ;

b. 

Em hãy dự đoán kết quả của phép biến đổi biểu thức \(1 + \dfrac{1}{{1 + \dfrac{1}{{1 + \dfrac{1}{{1 + \dfrac{1}{{1 + \dfrac{1}{x}}}}}}}}}\)

thành phân thức đại số và kiểm tra lại dự đoán đó.

Phương pháp:

 Áp dụng các phép toán cộng và chia hai phân thức đại số.

Lời giải:

Bài 54 trang 59 SGK Toán lớp 8 tập 1

Câu hỏi:

Tìm các giá trị của \(x\) để giá trị của các phân thức sau được xác định :

a.\(\eqalign{
& \,\,\,{{3x + 2} \over {2{x^2} - 6x}} \cr} \)

b. \(\eqalign{
& \,\,{5 \over {{x^2} - 3}} \cr} \)

Phương pháp:

Điều kiện xác định của phân thức là mẫu thức khác \(0\).

Lời giải:

Bài 55 trang 59 SGK Toán lớp 8 tập 1

Câu hỏi:

a.Cho phân thức \(\dfrac{{{x^2} + 2x + 1}}{{{x^2} - 1}}\).

b.Với giá trị nào của \(x\)  thì giá trị của phân thức được xác định?

Phương pháp:

a. Điều kiện xác định của phân thức là mẫu thức khác \(0\).

b.Áp dụng hằng đẳng thức bình phương một tổng, hiệu hai bình phương để phân tích tử thức và mẫu thức sau đó chia cả tử thức và mẫu thức với nhân tử chung giống nhau để rút gọn.

c.Kiểm tra giá trị của \(x\) có thỏa mãn điều kiện xác định của phân thức hay không. Nếu thỏa mãn thay giá trị của \(x\) vào phân thức rút gọn để tính giá trị của phân thức.

Lời giải:

Bài 56 trang 59 SGK Toán lớp 8 tập 1

Câu hỏi:

Cho phân thức \(\dfrac{{3{x^2} + 6x + 12}}{{{x^3} - 8}}\).

a.Với điều kiện nào của \(x\) thì giá trị của phân thức được xác định

b. Rút gọn phân thức.

c.Em có biết trên \(1c{m^2}\) bề mặt da của em có bao nhiêu con vi khuẩn không?

Tính giá trị của biểu thức đã cho tại \(x = \dfrac{{4001}}{{2000}}\) em sẽ tìm được câu trả lời thật đáng sợ. (Tuy nhiên trong số đó chỉ có \(20\% \) là vi khuẩn có hại).

Phương pháp:

a. Điều kiện xác định của phân thức là mẫu thức khác \(0\).

b. Rút gọn phân thức: Phân tích tử thức và mẫu thức sau đó chia cả tử thức và mẫu thức cho nhân tử chung giống nhau.

c.Thay \(x = \dfrac{{4001}}{{2000}}\) vào phân thức rút gọn để tính giá trị của phân thức.

Lời giải:

Sachbaitap.com