Bài 11, 12, 13, 14, 15 trang 74, 75 SGK Toán 8 tập 1 - Hình thang cân

Bài 11 trang 74 SGK Toán lớp 8 tập 1

Câu hỏi:

Tính độ dài các cạnh của hình thang cân \(ABCD\) trên giấy kẻ ô vuông (h.\(30\), độ dài cạnh ô vuông là \(1\,cm\)).

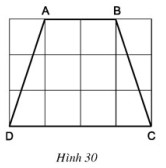
Phương pháp:

- Áp dụng định lý Pi-ta-go.

- Áp dụng tính chất hình thang cân: Trong hình thang cân hai cạnh bên bằng nhau.

Lời giải:

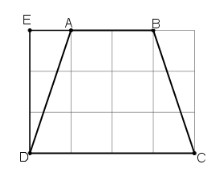
(Mỗi ô vuông là 1cm).

Ta lấy điểm E như trên hình vẽ.

Quan sát vào hình vẽ ta thấy :

+ AB = 2cm

+ CD = 4cm.

+ Tính AD :

Xét tam giác vuông ADE có AE = 1cm, DE = 3cm:

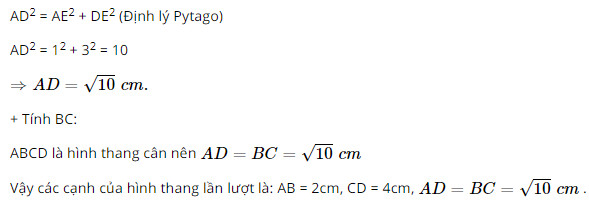
Bài 12 trang 74 SGK Toán lớp 8 tập 1

Câu hỏi:

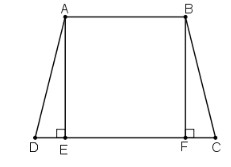
 Cho hình thang cân \(ABCD \;( AB // CD, AB < CD).\) Kẻ đường cao \(AE, BF\) của hình thang. Chứng minh rằng \(DE = CF.\)

Phương pháp:

+) Tính chất hình thang cân: hình thang cân có hai cạnh bên bằng nhau, hai góc kề \(1\) đáy bằng nhau.

+) Dấu hiệu nhận biết hai tam giác vuông bằng nhau: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

+) Tính chất hai tam giác bằng nhau: hai cạnh tương ứng bằng nhau.

Lời giải:

Vì hình thang ABCD cân

    AD = BC;

    Ĉ = D̂

Xét hai tam giác vuông AED và BFC có:

    AD = BC

    Ĉ = D̂

⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)

⇒ DE = CF.

Bài 13 trang 74 SGK Toán lớp 8 tập 1

Câu hỏi:

 Cho hình thang cân \(ABCD \;(AB // CD)\), \(E\) là giao điểm của hai đường chéo. Chứng minh rằng \(EA = EB, EC = ED.\)

Phương pháp: 

- Hình thang cân có hai cạnh bên bằng nhau, hai đường chéo bằng nhau.

- Hai tam giác bằng nhau có các góc tương ứng bằng nhau

- Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.

Lời giải:

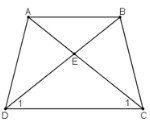
Do ABCD là hình thang cân nên:

    AD = BC;

    AC = BD;

Xét hai tam giác ADC và BCD, ta có:

    AD = BC (gt)

    AC = BD (gt)

    DC cạnh chung

⇒ ΔADC = ΔBCD (c.c.c)

⇒ ΔECD cân tại E

⇒ EC = ED.

Mà AC = BD

⇒ AC – EC = BD – ED

hay EA = EB.

Vậy EA = EB, EC = ED.

Bài 14 trang 75 SGK Toán lớp 8 tập 1

Câu hỏi:

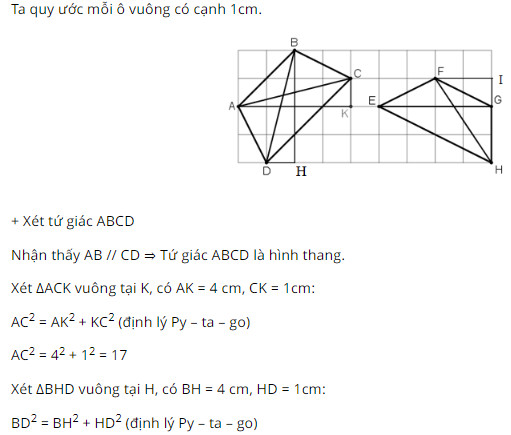
 Trong các tứ giác \(ABCD\) và \(EFGH\) trên giấy kẻ ô vuông (h.\(31\)), tứ giác nào là hình thang cân? Vì sao?

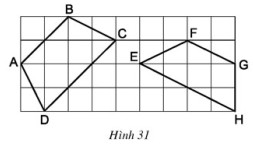
Phương pháp:

+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:

   - Chứng minh hai góc kề một đáy bằng nhau 

   - Chứng minh hai đường chéo bằng nhau

+ Định lý Pytago: \(ΔABC\) vuông tại \(A\) ta có: \(AB^2 + AC^2 = BC^2.\)

Lời giải:

Bài 15 trang 75 SGK Toán lớp 8 tập 1

Câu hỏi: 

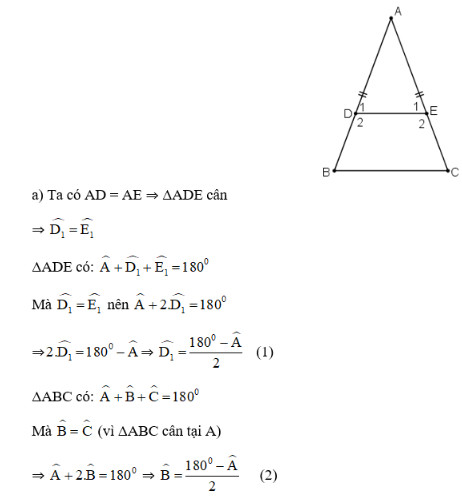
Cho \(\Delta ABC\) cân tại \(A.\) Trên các cạnh bên \(AB, AC\) lấy theo thứ tự các điểm \(D\) và \(E\) sao cho \(AD = AE.\)

a) Chứng minh rằng \(BDEC\) là hình thang cân.

b) Tính các góc của hình thang cân đó, biết rằng \(\widehat{A}=50^o\).

Phương pháp:

- Hình thang là tứ giác có hai cạnh đối song song.

- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.

- Định lí tổng ba góc của một tam giác bằng \(180^o\).

- Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.

Lời giải:

Sachbaitap.com