Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 51 SGK Toán 6 tập 1 Cánh Diều
Giải SGK Toán lớp 6 trang 51 tập 1 Cánh Diều - Bài 12. Ước chung và ước chung lớn nhất. Bài 1. Số 1 có phải là ước chung của hai số tự nhiên bất kì không? Vì sao? Bài 4. Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126, 150
Bài 1 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Số 1 có phải là ước chung của hai số tự nhiên bất kì không? Vì sao?
Phương pháp:
Số tự nhiên n là ước chung của hai số tự nhiên a và b nếu n vừa là ước của a vừa là ước của b.
Lời giải:
Số 1 là ước chung của hai số tự nhiên bất kì vì tất cả các số tự nhiên đều có ước là 1.
Bài 2 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Quan sát hai thanh sau:
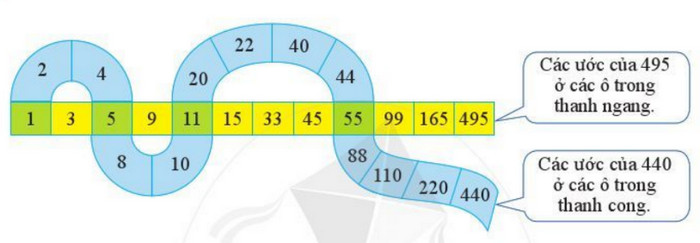
a) Viết tập hợp ƯC(440,495)
b) Tìm ƯCLN(440,495)
Phương pháp:
a) Ước chung của 440 và 495 là các ô nằm trên cả 2 thanh.
b) Tìm số lớn nhất trong tập hợp ƯC(440,495).
Lời giải:
a) Quan sát hình vẽ ta thấy
+ Các ước của 440 là: 1; 2; 4; 5; 8; 10; 11; 20; 22; 40; 44; 55; 88; 110; 220; 440
+ Các ước của 495 là: 1; 3; 5; 9; 11; 15; 33; 45; 55; 99; 165; 495
+ Các ước chung của 440 và 495 là: 1; 5; 11; 55.
Vậy ƯC(440, 495) = {1; 5; 11; 55}.
b) Trong các ước chung của 440 và 495, ta thấy 55 là số lớn nhất.
Vậy ƯCLN(440, 495) = 55.
Bài 3 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Tìm ước chung lớn nhất của từng cặp số trong 3 số sau đây:
a) 31, 22, 34
b) 105, 128, 135
Phương pháp:
a)
- Phân tích 3 số 31, 22, 34 ra thừa số nguyên tố.
- Chọn 2 trong 3 số 31, 22, 34.
- Tìm ƯCLN của 2 số đã chọn.
b)
- Phân tích 3 số 105,128,135 ra thừa số nguyên tố.
- Chọn 2 trong 3 số 105,128,135.
- Tìm ƯCLN của 2 số đã chọn.
Lời giải:
a)
31 = 31
22=2.11
34=2.17
+) ƯCLN(31,22) = 1
+) ƯCLN(31,34) = 1
+) ƯCLN (22,34) = 2
b)
\(105 = 3.5.7;128 = {2^7};135 = 3.3.3.5 = {3^3}.5\)
+) ƯCLN (105,128) = 1
+) ƯCLN (128,135) = 1
+) ƯCLN (105,135) = 15.
Bài 4 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126, 150
Phương pháp:
- Phân tích 3 số 126, 150 ra thừa số nguyên tố.
- Sử dụng tính chất: Ước chung của 126 và 150 là ước của ƯCLN(126,150).
Lời giải:
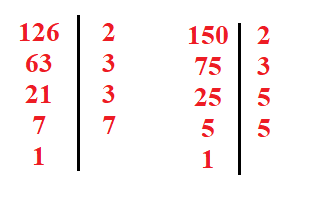
Do đó: 126 = 2 . 3 . 3 . 7 = 2 . 32 . 7
150 = 2 . 3 . 5 . 5 = 2 . 3 . 52
Các thừa số nguyên tố chung của 126 và 150 là 2 và 3
Số 2 có số mũ nhỏ nhất là 1; số 3 có số mũ nhỏ nhất là 1.
Do đó: ƯCLN(126, 150) = 21 . 31 = 2 . 3 = 6
Lại có 6 có các ước là 1; 2; 3; 6
Ước chung của 126 và 150 là ước của ƯCLN(126, 150) là 1; 2; 3; 6
Hay ƯC(126, 150) = {1; 2; 3; 6}
Vậy ƯCLN(126, 150) = 6; ƯC(126, 150) = {1; 2; 3; 6}.
Bài 5 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Rút gọn các phân số sau về phân số tối giản \(\frac{{60}}{{72}};\frac{{70}}{{95}};\frac{{150}}{{360}}\).
Phương pháp:
- Phân tích các số trên tử và mẫu ra thừa số nguyên tố.
- Tìm ƯCLN của tử và mẫu của mỗi phân số.
- Chia cả tử và mẫu cho ƯCLN tìm được.
Lời giải:
+) \(\begin{array}{l}60 = 2.2.3.5 = {2^2}.3.5\\72 = 2.2.2.3.3 = {2^3}{.3^2}\end{array}\)
=>ƯCLN(60,72) = 12.
=>\(\frac{{60}}{{72}} = \frac{60:12}{72:12}= \frac{5}{6}\).
+) \(\begin{array}{l}70 = 2.5.7\\95 = 5.19\end{array}\)
=>ƯCLN (70,95) = 5
=> \(\frac{{70}}{{95}} = \frac{70:5}{95:5}= \frac{{14}}{{19}}\).
+) \(\begin{array}{l}150 = {2.3.5^2}\\360 = {2^3}{.3^2}.5\end{array}\)
=> ƯCLN(150,360)=2.3.5=30
=> \(\frac{{150}}{{360}} = \frac{150:30}{360:30}= \frac{5}{{12}}\).
Bài 6 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Phân số \(\frac{4}{9}\) bằng các phân số nào trong các phân số sau: \(\frac{{48}}{{108}};\frac{{80}}{{180}};\frac{{60}}{{130}};\frac{{135}}{{270}}\).
Phương pháp:
- Rút gọn các phân số đã cho về phân số tối giản.
- Nếu phân số tối giản là \(\frac{4}{9}\) thì phân số ban đầu bằng \(\frac{4}{9}\).
Lời giải:
ƯCLN(48,108)=12
=>\(\frac{{48}}{{108}} = \frac{4}{9}\)
ƯCLN(80,180)=20
=> \(\frac{{80}}{{180}} = \frac{4}{9}\)
ƯCLN(60,130)=10
=>\(\frac{{60}}{{130}} = \frac{6}{{13}}\)
ƯCLN(135,270)=135
=>\(\frac{{135}}{{270}} = \frac{1}{2}\)
Phân số \(\frac{4}{9}\) bằng các phân số \(\frac{{48}}{{108}};\frac{{80}}{{180}}\).
Bài 7 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Một nhóm gồm 24 bạn nữ và 30 bạn nam tham gia một số trò chơi. Có thể chia các bạn thành nhiều nhất bao nhiêu đội chơi sao cho số bạn nam cũng như số bạn nữ được chia đều vào các đội?
Phương pháp:
- Gọi số đội được chia.
- Số độ phải là ƯCLN của 24 và 30.
- Tìm ƯCLN(24,30).
Lời giải:
Giả sử a là số đội chơi được chia. (a ∈ )
Vì a là lớn nhất (phải chia nhiều đội nhất) và số bạn nam cũng như số bạn nữ được chia đều vào các đội nên khi đó a là ước chung lớn nhất của 24 và 30.
Ta có: 24 = 3 . 8 = 3 . 23 ; 30 = 3 . 10 = 3 . 2 . 5
(Các thừa số chung là 2; 3 và đều có số mũ nhỏ nhất là 1)
Khi đó: ƯCLN(24, 30) = 2 . 3 = 6 hay a = 6.
Vậy có thể chia các bạn nhiều nhất thành 6 đội.
Bài 8 trang 51 SGK Toán 6 tập 1 - Cánh Diều
Một khu đất có dạng hình chữ nhật với chiều dài 48m, chiều rộng 42m. Người ta muốn chia khu đất ấy thành những mảnh hình vuông bằng nhau (với độ dài cạnh đo theo đơn vị mét là số tự nhiên) để trồng các loại rau. Có thể chia được bằng bao nhiêu cách? Với cách chia nào thì cạnh của mảnh đất hình vuông là lớn nhất và bằng bao nhiêu?
Phương pháp:
- Gọi số cách chia mảnh đất và độ dài cạnh hình vuông lớn nhất.
- Tìm số ước chung của 48 và 42: Số cách chia.
- Tìm ƯCLN(42, 48): độ dài cạnh lớn nhất.
Lời giải:
Gọi: a là số cách chia mảnh đất thành các mảnh hình vuông bằng nhau
b (m) là độ dài cạnh của mảnh đất hình vuông được chia theo cách chia lớn nhất a,b ∈
Theo yêu cầu bài ra thì khi đó:
+ a là số các ước chung của 48 và 42
+ b là ước chung lớn nhất của 48 và 42
Ta có: 42 = 2 . 21 = 2 . 3 . 7
48 = 16 . 3 = 24 . 3
Do đó: ƯCLN(42, 48) = 2 . 3 = 6 hay b = 6 m
Mà Ư(6) = {1; 2; 3; 6) Nên ƯC(42, 48) = {1; 2; 3; 6}
Do đó có 4 ước chung của 42 và 48 hay a = 4.
Vậy:
+ Số cách chia thành những mảnh hình vuông bằng nhau là 4 cách.
+ Với cách chia có độ dài cạnh là 6m thì cạnh của mảnh đất hình vuông là lớn nhất.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4 trang 104, 105, 106 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 trang 102, 103 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6, 7 trang 92, 93 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6 trang 87, 88 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6 trang 83 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Hoạt động thực hành và trải nghiệm chủ đề 3. Sắp xếp các vị trí thẳng hàng
- Bài tập cuối chương 6
- Bài 5. Góc
- Bài 4. Tia
- Bài 3. Đoạn thẳng
- Bài 2. Hai đường thẳng cắt nhau. Hai đường thẳng song song
- Bài 1. Điểm. Đường thẳng
- Chương 6. Hình học phẳng
- Hoạt động thực hành và trải nghiệm. Chủ đề 2. Chỉ số khối cơ thể (BMI)
- Bài tập cuối chương 5
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
