Giải bài 1, 2, 3, 4, 5 trang 90, 91 SGK Toán 9 Cánh Diều tập 1

Bài 1 trang 90 SGK Toán 9 tập 1 - Cánh Diều

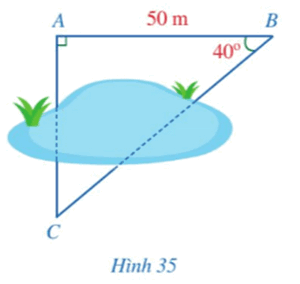
Hình 35 mô tả ba vị trí \(A,B,C\) là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ \(C\) đến \(A\) và từ \(C\) đến \(B\). Biết \(AB = 50m\), \(\widehat {ABC} = 40^\circ \). Tính khoảng cách \(CA\) và \(CB\) (làm tròn kết quả đến hàng đơn vị của mét).

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

Xét ∆ABC vuông tại A, ta có:

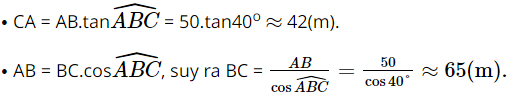
Bài 2 trang 91 SGK Toán 9 tập 1 - Cánh Diều

Để ước lượng chiều cao của một cây trong sân trường, bạn Hoàng đứng ở sân trường (theo phương thẳng đứng), mặt bạn Hoàng đặt tại vị trí \(C\) cách mặt đất một khoảng \(CB = DH = 1,64m\) và cách cây một khoảng \(CD = BH = 6m\). Tính chiều cao \(AH\) của cây (làm tròn kết quả đến hàng phần trăm của mét), biết góc nhìn \(ACD\) bằng \(38^\circ \) minh họa ở Hình 36. 

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

Xét ∆ACD vuông tại D, ta có:

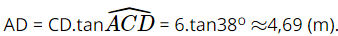
Ta có AG = AD + DH ≈ 4,69 + 1,64 = 6,33 (m).

Vậy chiều cao AH của cây khoảng 6,33 m.

Bài 3 trang 91 SGK Toán 9 tập 1 - Cánh Diều

Trong công việc, người ta cần ước lượng khoảng cách từ vị trí \(O\) đến khu đất có dạng hình thang \(MNPQ\) nhưng không thể đo được trực tiếp, khoảng cách đó được tính bằng khoảng cách từ \(O\) đến đường thẳng \(MN\). Người ta chọn vị trí \(A\) ở đáy \(MN\) và đo được \(OA = 18m,\widehat {OAN} = 44^\circ \) (Hình 37). Tính khoảng cách từ vị trí \(O\) đến khu đất (làm tròn kết quả đến hàng phần mười của mét).

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

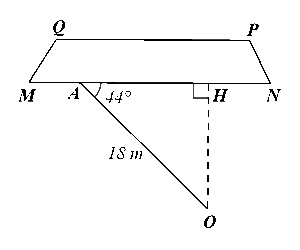
Gọi H là chân đường vuông góc kẻ từ O đến MN.

Xét ∆OAH vuông tại H, ta có: OH = OA.sinA = 18.sin44° ≈ 12,5 (m).

Vậy khoảng cách từ vị trí O đến khu đất khoảng 12,5 m.

Bài 4 trang 91 SGK Toán 9 tập 1 - Cánh Diều

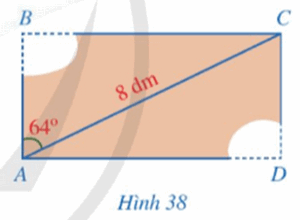
Một mảnh gỗ có dạng hình chữ nhật \(ABCD\) với đường chéo \(AC = 8dm\). Do bảo quản không tốt nên mảnh gỗ bị hỏng phía hai đỉnh \(B\) và \(D\). Biết \(\widehat {BAD} = 64^\circ \) (Hình 38). Người ta cần biết độ dài \(AB\) và \(AD\) để khôi phục mảnh gỗ ban đầu. Độ dài \(AB,AD\) bằng bao nhiêu decimét (làm tròn kết quả đến hàng phần mười)? 

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

Xét ∆ABC vuông tại B, ta có:

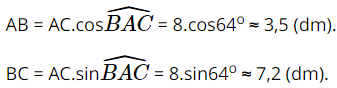
Do ABCD là hình chữ nhật nên AD = BC ≈ 7,2 dm.

Vậy AB ≈ 3,5 dm và AD ≈ 7,2 dm.

Bài 5 trang 91 SGK Toán 9 tập 1 - Cánh Diều

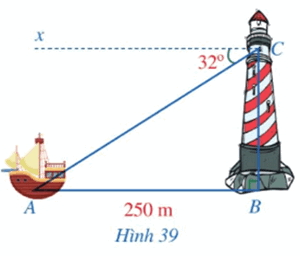
Trên mặt biển, khi khoảng cách \(AB\) từ ca nô đến chân tháp hải đăng là 250m, một người đứng trên tháp hải đăng đó nhìn về phía ca nô theo phương \(CA\) tạo với phương nằm ngang \(Cx\) một góc là \(\widehat {ACx} = 32^\circ \) (Hình 39). Tính chiều cao của tháp hải đăng (làm tròn kết quả đến hàng phần mười của mét), biết \(AB//Cx\) và độ cao từ tầm mắt của người đó đến đỉnh tháp là 3,2m. 

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

Vì Cx // AB nên 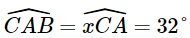(so le trong).

Xét ∆ABC vuông tại B, ta có: BC = AB.tan  = 250.tan32o ≈ 156,2 (m).

Vậy chiều cao của tháp là khoảng 156,2 + 3,2 = 159,4 (m).

Sachbaitap.com