Giải bài 1.19, 1.20, 1.21, 1.22, 1.23, 1.24, 1.25, 1.26, 1.27, 1.28 trang 24 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 24 Kết nối tri thức tập 1. Bài 1.25: Tìm số tự nhiên N có hai chữ số, biết rằng nếu viết thêm chữ số 3 vào giữa hai chữ số của số N thì được một số lớn hơn số 2N là 585 đơn vị, và nếu viết hai chữ số của số N theo thứ tự ngược lại thì được một số nhỏ hơn số N là 18 đơn vị.
Xem thêm: Bài tập cuối chương 1
Bài 1.19 trang 24 SGK Toán 9 tập 1 - Kết nối tri thức
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}5x + 7y = - 1\\3x + 2y = - 5\end{array} \right.?\)
A. \(\left( { - 1;1} \right).\)
B. \(\left( { - 3;2} \right).\)
C. \(\left( {2; - 3} \right).\)
D. \(\left( {5;5} \right).\)
Phương pháp:
Đây là câu hỏi trắc nghiệm nên có thể sử dụng MTCT để giải.
Giải hệ phương trình \(\left\{ \begin{array}{l}5x + 7y = - 1\\3x + 2y = - 5\end{array} \right.\) qua MTCT ta được kết quả \(\left\{ \begin{array}{l}x = - 3\\y = 2\end{array} \right.\) từ đó kết luận nghiệm \(\left( { - 3;2} \right).\)
Lời giải:
Đáp án đúng là: B
Nhân hai vế của phương trình thứ nhất cho 3 và chia hai vế của phương trình thứ hai cho 5, ta được: 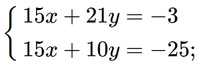
Trừ từng vế hai phương trình của hệ mới, ta được 11y = 22 hay y = 2.
Thế y = 2 vào phương trình thứ hai của hệ đã cho, ta có 3x + 2 . 2 = –5 hay 3x = –9, suy ra x = –3.
Do đó, hệ phương trình đã cho có nghiệm là (–3; 2).
Vậy ta chọn đáp án B.
Bài 1.20 trang 24 SGK Toán 9 tập 1 - Kết nối tri thức
Trên mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {1;2} \right),B\left( {5;6} \right),C\left( {2;3} \right),D\left( { - 1; - 1} \right).\) Đường thẳng \(4x - 3y = - 1\) đi qua hai điểm nào trong các điểm đã cho?
A. A và B;
B. B và C;
C. C và D;
D. D và A.
Phương pháp:
Thay tọa độ các điểm vào đường thẳng kiểm tra tính đúng sai, nếu thu được kết quả đúng ta sẽ được điểm thuộc đường thẳng.
Lời giải:
Đáp án đúng là: C
• Thay x = 1; y = 2 vào phương trình đường thẳng, ta có:
4 . 1 – 3 . 2 = 4 – 6 = –2 ≠ –1.
Suy ra đường thẳng 4x – 3y = –1 không đi qua A(1; 2).
Do đó, loại đáp án A và D.
• Thay x = 5; y = 6 vào phương trình đường thẳng, ta có:
4 . 5 – 3 . 6 = 20 – 18 = 2 ≠ –1.
Suy ra đường thẳng 4x – 3y = –1 không đi qua B(5; 6).
Do đó, loại đáp án B.
• Thay x = 2; y = 3 vào phương trình đường thẳng, ta có:
4 . 2 – 3 . 3 = 8 – 9 = –1.
Suy ra đường thẳng 4x – 3y = –1 không đi qua C(2; 3).
Do đó, ta chọn đáp án C.
Bài 1.21 trang 24 SGK Toán 9 tập 1 - Kết nối tri thức
Hệ phương trình \(\left\{ \begin{array}{l}1,5x - 0,6y = 0,3\\ - 2x + y = - 2\end{array} \right.\)
A. Có nghiệm là \(\left( {0; - 0,5} \right).\)
B. Có nghiệm là \(\left( {1;0} \right).\)
C. Có nghiệm là \(\left( { - 3; - 8} \right).\)
D. Vô nghiệm.
Phương pháp:
Đây là câu hỏi trắc nghiệm nên có thể sử dụng MTCT để giải.
Giải hệ phương trình \(\left\{ \begin{array}{l}1,5x - 0,6y = 0,3\\ - 2x + y = - 2\end{array} \right.\) qua MTCT ta được kết quả \(\left\{ \begin{array}{l}x = - 3\\y = - 8\end{array} \right.\) từ đó kết luận nghiệm \(\left( { - 3; - 8} \right).\)
Lời giải:
Chia hai vế của phương trình thứ nhất cho 0,3 và nhân hai vế của phương trình thứ hai với 2, ta được: 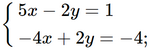
Cộng từng vế hai phương trình của hệ mới, ta được x = −3.
Thế x = −3 vào phương trình thứ hai của hệ đã cho, ta có
(−2) . (−3) + y = –2 hay 6 + y = –2, suy ra y = –8.
Do đó, hệ phương trình đã cho có nghiệm là (−3; −8).
Bài 1.22 trang 24 SGK Toán 9 tập 1 - Kết nối tri thức
Hệ phương trình \(\left\{ \begin{array}{l}0,6x + 0,3y = 1,8\\2x + y = - 6\end{array} \right.\)
A. Có 1 nghiệm.
B. Vô nghiệm.
C. Có vô số nghiệm.
D. Có hai nghiệm.
Phương pháp:
Đây là câu hỏi trắc nghiệm nên có thể sử dụng MTCT để giải.
Giải hệ phương trình \(\left\{ \begin{array}{l}0,6x + 0,3y = 1,8\\2x + y = - 6\end{array} \right.\) qua MTCT, màn hình hiện kết quả “No solution” từ đó kết luận vô nghiệm.
Lời giải:
Đáp án đúng là: B
Chia hai vế của phương trình thứ nhất cho 0,3 ta được: 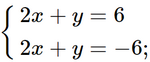
Trừ từng vế hai phương trình của hệ mới, ta được 0x + 0y = 12. (1)
Do không có giá trị nào của x và y thỏa mãn hệ thức (1) nên hệ phương trình đã cho vô nghiệm.
Bài 1.23 trang 24 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các hệ phương trình:
a) \(\left\{ \begin{array}{l}2x + 5y = 10\\\frac{2}{5}x + y = 1;\end{array} \right.\)
b) \(\left\{ \begin{array}{l}0,2x + 0,1y = 0,3\\3x + y = 5;\end{array} \right.\)
c) \(\left\{ \begin{array}{l}\frac{3}{2}x - y = \frac{1}{2}\\6x - 4y = 2.\end{array} \right.\)
Phương pháp:
Ta có thể giải hệ bằng hai phương pháp thế hoặc cộng đại số.
Lời giải:
a) Nhân hai vế của phương trình thứ nhất với 5, ta được: 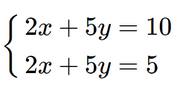
Trừ từng vế hai phương trình của hệ mới, ta được 0x + 0y = 5. (1)
Do không có giá trị nào của x và y thỏa mãn hệ thức (1) nên hệ phương trình đã cho vô nghiệm.
b) Nhân hai vế của phương trình thứ nhất với 10, ta được: 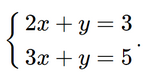
Trừ từng vế hai phương trình của hệ mới, ta được x = 2.
Thế x = 2 vào phương trình thứ hai của hệ đã cho, ta có
3 . 2 + y = 5 hay 6 + y = 5, suy ra y = –1.
Vậy hệ phương trình đã cho có nghiệm là (2; –1).
c) Nhân hai vế của phương trình thứ nhất với 2 và chia hai vế của phương trình thứ nhất cho 2, ta được: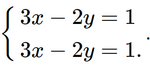
Trừ từng vế hai phương trình của hệ mới, ta được 0x = 0. Phương trình nghiệm đúng với mọi x ∈ ℝ.
Ta có 3x – 2y = 1 hay 2y = 3x – 1, suy ra 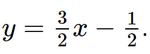
Vậy hệ phương trình có vô số nghiệm. Các nghiệm của hệ được viết như sau 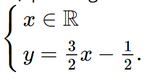
Bài 1.24 trang 24 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các hệ phương trình:
a) \(\left\{ \begin{array}{l}0,5x + 2y = - 2,5\\0,7x - 3y = 8,1;\end{array} \right.\)
b) \(\left\{ \begin{array}{l}5x - 3y = - 2\\14x + 8y = 19;\end{array} \right.\)
c) \(\left\{ \begin{array}{l}2\left( {x - 2} \right) + 3\left( {1 + y} \right) = - 2\\3\left( {x - 2} \right) - 2\left( {1 + y} \right) = - 3.\end{array} \right.\)
Phương pháp:
Ta có thể giải hệ bằng hai phương pháp thế hoặc cộng đại số.
Lời giải:
a) Nhân hai vế của phương trình thứ nhất với 3 và nhân hai vế của phương trình thứ hai với 2, ta được: 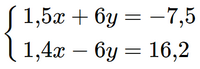
Trừ từng vế hai phương trình của hệ mới, ta được 2,9x = 8,7, suy ra x = 3.
Thế x = 3 vào phương trình thứ nhất của hệ đã cho, ta có
0,5 . 3 + 2y = –2,5 hay 2y = –4, suy ra y = –2.
Vậy hệ phương trình đã cho có nghiệm là (3; –2).

Trừ từng vế hai phương trình của hệ mới, ta được 13b = 0, suy ra b = 0.
Thế x = 0 vào phương trình thứ nhất của hệ (I), ta có
2a + 3 . 0 = –2 hay 2a = –2, suy ra a = –1.
• Với a = –1 thì x – 2 = –1, suy ra x = 1.
• Với b = 0 thì 1 + y = 0, suy ra y = –1.
Vậy hệ phương trình đã cho có nghiệm là (1; –1).
Bài 1.25 trang 25 SGK Toán 9 tập 1 - Kết nối tri thức
Tìm số tự nhiên N có hai chữ số, biết rằng nếu viết thêm chữ số 3 vào giữa hai chữ số của số N thì được một số lớn hơn số 2N là 585 đơn vị, và nếu viết hai chữ số của số N theo thứ tự ngược lại thì được một số nhỏ hơn số N là 18 đơn vị.
Phương pháp:
Số tự nhiên N có hai chữ số nên N có dạng \(\overline {ab} \left( {0 < a \le 9;0 \le b \le 9;a,b \in \mathbb{N}} \right)\) và \(\overline {ab} = 10a + b.\)
Tương tự với số mới khi thêm số 3 vào giữa a và b thì ta có số mới \(\overline {a3b} \) và \(\overline {a3b} = 100a + 30 + b.\)
Từ đó ta biểu thị mối liên hệ giữa các số để ra hệ phương trình chứa a và b, giải hệ ta sẽ tìm được số N.
Lời giải:
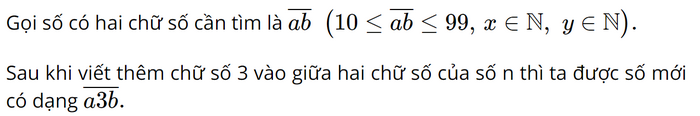
Nếu viết thêm chữ số 3 vào giữa hai chữ số của số n thì được một số lớn hơn số 2n là 585 đơn vị nên ta có phương trình
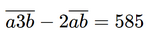
100a + 30 + b − 2(10a + b) = 585
100a + 30 + b − 20a − 2b = 585
80a – b = 555. (1)

10a + b − (10b + a) = 18
10a + b − 10b − a = 18
a – b = 2. (2)
Từ (1) và (2) ta có hệ phương trình 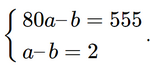
Trừ từng vế của hai phương trình ta có
(80a − b) − (a − b) = 555 − 2 hay 79a = 55, suy ra a = 7 (thỏa mãn điều kiện).
• Với a = 7 thay vào phương trình thứ hai ta được b = 5 (thỏa mãn điều kiện).
Vậy số tự nhiên n có hai chữ số cần tìm là 75.
Bài 1.26 trang 25 SGK Toán 9 tập 1 - Kết nối tri thức
Trên cánh đồng có diện tích 160 ha của một đơn vị sản xuất, người ta dành 60 ha để cấy thí điểm giống lúa mới, còn lại vẫn cấy giống cũ. Khi thu hoạch, đầu tiên người ta gặt 8 ha giống lúa cũ và 7 ha giống lúa mới để đối chứng. Kết quả là 7 ha giống lúa mới cho thu hoạch nhiều hơn 8 ha giống lúa cũ là 2 tấn thóc. Biết rằng tổng số thóc (cả hai giống) thu hoạch cả vụ trên 160 ha là 860 tấn. Hỏi năng suất của mỗi giống lúa trên 1 ha là bao nhiêu tấn thóc?
Phương pháp:
Đề cho tổng diện tích 160 ha, biết diện tích cấy giống lúa mới là 60 ha, ta cần tính diện tích trồng lúa cũ: \(160 - 60 = 100\left( {ha} \right).\) Gọi năng suất của mỗi giống lúa mới và cũ trên 1 ha là x,y (tấn thóc) \(\left( {x,y > 0} \right).\)
Chú ý: Năng suất lúa x diện tích đất trồng (số ha) = số thóc thu được.
Từ đó ta xây dựng mối liên hệ giữa các ẩn để ra hệ phương trình chứa x và y, từ đó giải hệ ta sẽ tìm được x và y.
Lời giải:
Số ha cấy lúa cũ là: 160 – 60 = 100 (ha).
Gọi năng suất của mỗi giống lúa trên 1 ha là x, y (tấn thóc) (x > 0, y > 0).
Số lúa cũ thu được trên 8 ha giống lúa cũ là 8x (tấn thóc).
Số lúa mới thu được trên 7 ha giống lúa mới là 7y (tấn thóc).
Kết quả 7 ha giống lúa mới cho thu hoạch nhiều hơn 8 ha giống lúa cũ là 2 tấn thóc nên ta có phương trình 7y − 8x = 2. (1)
Số lúa cũ thu được trên 100 ha giống lúa cũ là 100x (tấn thóc).
Số lúa mới thu được trên 60 ha giống lúa mới là 60y (tấn thóc).
Tổng số thóc (cả hai giống) thu hoạch cả vụ trên 160 ha là 860 tấn nên ta có phương trình 100x + 60y = 860 hay 5x + 3y = 43. (2)
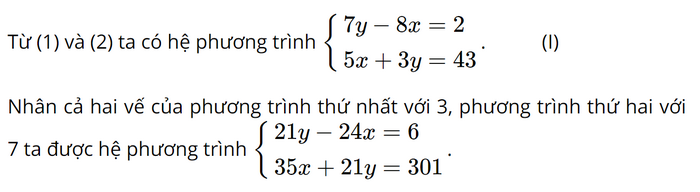
Trừ từng vế của hai phương trình ta được
(21y − 24x) − (35x + 21y) = 6 − 301 hay −59x = −295 nên x = 5 (thỏa mãn điều kiện).
Thế x = 5 vào phương trình thứ hai của hệ (I), ta có
5 . 5 + 3y = 43 hay 3y = 18, suy ra y = 6 (thỏa mãn điều kiện).
Vậy trên 1 ha, năng suất của mỗi giống lúa cũ là 5 tấn thóc, năng suất của mỗi giống lúa mới là 6 tấn thóc.
Bài 1.27 trang 25 SGK Toán 9 tập 1 - Kết nối tri thức
Hai vật chuyển động đều trên một đường tròn đường kính 20 cm, xuất phát cùng một lúc, từ cùng 1 điểm. Nếu chuyển động ngược chiều thì cứ sau 4 giây chúng lại gặp nhau. Nếu chuyển động cùng chiều thì cứ 20 giây chúng lại gặp nhau. Tính vận tốc (cm/s) của mỗi vật.
Phương pháp:
Cần tính quãng đường chuyển động của vật dựa vào chu vi của hình tròn.
Chu vi của hình tròn là \(20.3,14 = 62,8\left( {cm} \right)\)
Không mất tổng quát, xét trường hợp vật thứ nhất chuyển động nhanh hơn vật thứ hai.
Đối với trường hợp 2 vật chuyển động cùng chiều và cùng thời điểm cùng xuất phát một lúc đến thời điểm gặp nhau đầu tiên thì quãng đường vật thứ nhất đi được sẽ nhiều hơn vật thứ hai bằng đúng 1 chu vi đường tròn.
Đối với trường hợp 2 vật chuyển động ngược chiều và cùng thời điểm cùng xuất phát một lúc đến thời điểm gặp nhau đầu tiên thì quãng đường cả hai vật đi được bằng đúng 1 chu vi đường tròn.
Lời giải:
Chu vi của hình tròn là 20 . 3,14 = 62,8 (cm).
Không mất tổng quát, xét trường hợp vật thứ nhất chuyển động nhanh hơn vật thứ hai.
Gọi vận tốc (cm/s) của mỗi vật là x, y (x > y > 0).
Quãng đường vật thứ nhất đi được sau 20 giây là 20x (cm).
Quãng đường vật thứ nhất đi được sau 20 giây là 20y (cm).
Hai vật chuyển động cùng chiều thì cứ 20 giây chúng lại gặp nhau nên ta có phương trình 20x − 20y = 62,8 hay x – y = 3,14. (1)
Quãng đường vật thứ nhất đi được sau 4 giây là 4x (cm).
Quãng đường vật thứ nhất đi được sau 4 giây là 4y (cm).
chuyển động ngược chiều thì cứ sau 4 giây chúng lại gặp nhau nên ta có phương trình
4x + 4y = 62,84 hay x + y = 15,7. (2)
Từ (1) và (2) ta có hệ phương trình 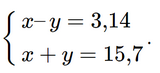
Cộng từng vế của hai phương trình ta có
x – y + x + y = 3,14 + 15,7 hay 2x = 18,84, suy ra x = 9,42 (thỏa mãn điều kiện).
Thay x = 9,42 vào phương trình đầu ta được y = 6,28 (thỏa mãn điều kiện).
Vậy vận tốc của hai vật lần lượt là 9,42 cm/s và 6,28 cm/s.
Bài 1.28 trang 25 SGK Toán 9 tập 1 - Kết nối tri thức
Một người mua hai loại hàng và phải trả tổng cộng là 21,7 triệu đồng, kể cả thuế giá trị gia tăng (VAT) tới mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 21,8 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?
Phương pháp:
Cần tính quãng đường chuyển động của vật dựa vào chu vi của hình tròn.
Chu vi của hình tròn là \(20.3,14 = 62,8\left( {cm} \right)\)
Không mất tổng quát, xét trường hợp vật thứ nhất chuyển động nhanh hơn vật thứ hai.
Đối với trường hợp 2 vật chuyển động cùng chiều và cùng thời điểm cùng xuất phát một lúc đến thời điểm gặp nhau đầu tiên thì quãng đường vật thứ nhất đi được sẽ nhiều hơn vật thứ hai bằng đúng 1 chu vi đường tròn.
Đối với trường hợp 2 vật chuyển động ngược chiều và cùng thời điểm cùng xuất phát một lúc đến thời điểm gặp nhau đầu tiên thì quãng đường cả hai vật đi được bằng đúng 1 chu vi đường tròn.
Lời giải:
Gọi số tiền người mua hàng phải trả đối với loại hàng thứ nhất và loại hàng thứ hai không kể thuế VAT là x, y (x, y > 0) (triệu đồng)
Khi thuế giá trị gia tăng (VAT) tới mức 10% đối với loại hàng thứ nhất thì giá tiền của loại hàng thứ nhất là 110%x = 1,1x.
8% đối với loại hàng thứ hai thì giá tiền của loại hàng thứ hai là 108%y = 1,08y.
Người mua hàng phải trả tổng cộng là 21,7 triệu đồng nên ta có phương trình
1,1x + 1,08y = 21,7. (1)
Nếu thuế VAT là 9% đối với cả hai loại hàng thì giá tiền của loại hàng thứ nhất là
109%x = 1,09x.
Giá tiền của loại hàng thứ hai là 109%y = 1,09y.
Người đó phải trả tổng cộng 21,8 triệu đồng nên ta có phương trình
1,09x + 1,09y = 21,8 hay x + y = 20. (2)
Từ (1) và (2), ta có hệ phương trình 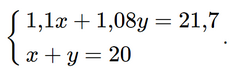
Từ phương trình thứ hai ta có x = 20 – y. Thay vào phương trình nhất ta được:
1,1(20 – y) + 1,08y = 21,7 hay −0,02y = 0,3 nên y = 15 (thỏa mãn điều kiện).
Với y = 15 thì x = 5 (thỏa mãn điều kiện).
Vậy nếu không kể thuế VAT thì người đó phải trả 5 triệu đồng cho mặt hàng thứ nhất và 15 triệu cho mặt hàng thứ hai.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 114, 115 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.32, 5.33, 5.34, 5.35, 5.36, 5.37, 5.38, 5.39, 5.40 trang 113 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.28, 5.29, 5.30, 5.31 trang 110 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.24, 5.26, 5.27 trang 107 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Pha chế dung dịch theo nồng độ yêu cầu
- Bài tập cuối chương 5
- Luyện tập chung trang 108
- Bài 17: Vị trí tương đối của hai đường tròn
- Bài 16: Vị trí tương đối của đường thẳng và đường tròn
- Luyện tập chung trang 96
- Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Bài 14: Cung và dây của một đường tròn
- Bài 13: Mở đầu về đường tròn
- Chương V: Đường tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!