Giải bài 2.1, 2.2, 2.3, 2.4, 2.5 trang 30 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 30 Kết nối tri thức tập 1. Bài 2.4: Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như hình 2.3. Biết diện tích đất làm nhà là (100{m^2}.) Hỏi x bằng bao nhiêu mét?
Bài 2.1 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các phương trình sau:
a) \(x\left( {x - 2} \right) = 0;\)
b) \(\left( {2x + 1} \right)\left( {3x - 2} \right) = 0.\)
Phương pháp:
Phương trình dạng \(A\left( x \right).B\left( x \right) = 0\) thì \(A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\)
Lời giải:
a) x(x – 2) = 0
Suy ra x = 0 hoặc x – 2 = 0
Do đó x = 0 hoặc x = 2.
Vậy phương trình đã cho có nghiệm x = 0 và x = 2.
b) (2x + 1)(3x – 2) = 0
Ta giải hai phương trình sau:

Bài 2.2 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các phương trình sau:
a) \(\left( {{x^2} - 4} \right) + x\left( {x - 2} \right) = 0;\)
b) \({\left( {2x + 1} \right)^2} - 9{x^2} = 0.\)
Phương pháp:
Cần đưa phương trình đã cho về dạng \(A\left( x \right).B\left( x \right) = 0\) thì \(A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\)
Bằng cách sử dụng phương pháp phân tích đa thức thành nhân tử thông qua đặt nhân tử chung hoặc sử dụng hằng đẳng thức đáng nhớ.
Lời giải:
a) (x2 – 4) + x(x – 2) = 0
(x – 2)(x + 2) + x(x – 2) = 0
(x – 2)(x + 2 + x) = 0
(x – 2)(2x + 2) = 0.
Ta giải hai phương trình sau:
⦁ x – 2 = 0, suy ra x = 2.
⦁ 2x + 2 = 0 hay 2x = –2, suy ra x = –1.
Vậy phương trình đã cho có nghiệm là x = 2 và x = –1.
b) (2x + 1)2 – 9x2 = 0
(2x + 1)2 – (3x)2 = 0
(2x + 1 – 3x)(2x + 1 + 3x) = 0
(–x + 1)(5x + 1) = 0.
Ta giải hai phương trình sau:
⦁ –x + 1 = 0, suy ra x = 1.

Bài 2.3 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các phương trình sau:
a) \(\frac{2}{{2x + 1}} + \frac{1}{{x + 1}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};\)
b) \(\frac{1}{{x + 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{{3x}}{{{x^3} + 1}}.\)
Phương pháp:
Các bước giải phương trình chứa ẩn ở mẫu
- Bước 1: Tìm ĐKXĐ
- Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu
- Bước 3: Giải phương trình vừa thu được
- Bước 4: Kết luận (đối chiếu ĐKXĐ).
Lời giải:

Khử mẫu của phương trình, ta được: 2(x + 1) + 2x + 1 = 3. (*)
Giải phương trình (*):
2(x + 1) + 2x + 1 = 3
2x + 2 + 2x + 1 = 3
4x + 3 = 3
4x = 0
x = 0.
Giá trị x = 0 thỏa mãn điều kiện của phương trình đã cho.
Vậy phương trình đã cho có nghiệm là x = 0.
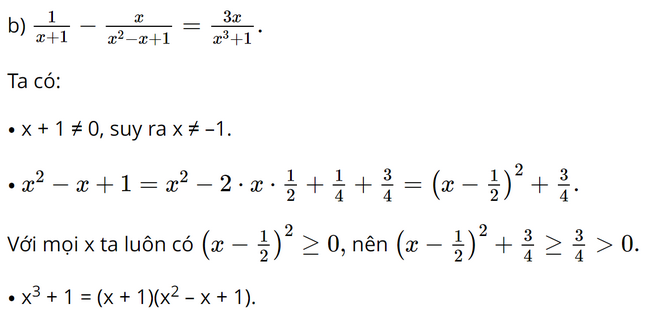
Khử mẫu của phương trình, ta được: x2 – x + 1 – x(x + 1) = 3x. (**)
Giải phương trình (**):
x2 – x + 1 – x(x + 1) = 3x
x2 – x + 1 – x2 – x – 3x = 0
–5x = –1

Bài 2.4 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức
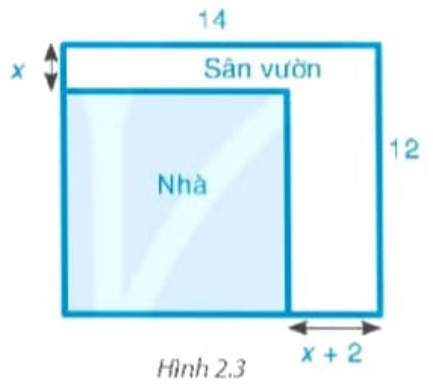
Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như hình 2.3. Biết diện tích đất làm nhà là \(100{m^2}.\) Hỏi x bằng bao nhiêu mét?
Phương pháp:
Ta biểu diễn các cạnh của phần đất làm nhà theo độ dài của mảnh đất.
Viết phương trình biểu diễn diện tích phần đất làm nhà.
Giải phương trình để tìm x.
Lời giải:
Chiều dài của phần đất làm nhà là: 14 – (x + 2) = 12 – x (m). Điều kiện x < 12.
Chiều rộng của phần đất làm nhà là: 12 – x (m).
Diện tích đất làm nhà là: (12 – x)2 (m2).
Theo bài, diện tích đất làm nhà là 100 m2 nên ta có phương trình:
(12 – x)2 = 100. (*)
Giải phương trình (*):
(12 – x)2 = 100
(12 – x)2 – 102 = 0
(12 – x – 10)(12 – x + 10) = 0
(2 – x)(22 – x) = 0
Suy ra 2 – x = 0 hoặc 22 – x = 0
Do đó x = 2 hoặc x = 22.
Ta thấy x = 2 thỏa mãn điều kiện x < 12.
Vậy x = 2.
Bài 2.5 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức
Hai người cùng làm chung một công việc thì xong trong 8 giờ. Hai người cùng làm được 4 giờ thì người thứ nhất bị điều đi làm công việc khác. Người thứ hai tiếp tục làm việc trong 12 giờ nữa thì xong công việc. Gọi x là thời gian người thứ nhất làm một mình xong công việc (đơn vị tính là giờ, \(x > 0\)).
a) Hãy biểu thị theo x:
- Khối lượng công việc mà người thứ nhất làm được trong 1 giờ;
- Khối lượng công việc mà người thứ hai làm được trong 1 giờ;
b) Hãy lập phương trình theo x và giải phương trình đó. Sau đó cho biết, nếu làm một mình thì mỗi người phải làm trong bao lâu mới xong công việc đó.
Phương pháp:
Cần quan tâm các các dữ liệu về các đại lượng sau (thời gian, năng suất công nhân (lượng công việc làm được trong mỗi giờ), số phần công việc thay đổi theo từng dữ kiện.
Tính năng suất trong một giờ công nhân thứ nhất được mấy phần của công việc \(1:x\)
Tính năng suất trong một giờ cả hai công nhân làm được bao nhiêu phần của công việc \(1:8\)
Dẫn đến mỗi giờ công nhân thứ hai sẽ làm được \(1:8 - 1:x\)
Dựa theo dữ kiện của bài toán ta sẽ lập được phương trình chứa x và giải được x rồi kết luận bài toán.
Chú ý: Năng suất của công nhân = 1 : Thời gian làm việc
Lời giải:

Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 114, 115 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.32, 5.33, 5.34, 5.35, 5.36, 5.37, 5.38, 5.39, 5.40 trang 113 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.28, 5.29, 5.30, 5.31 trang 110 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.24, 5.26, 5.27 trang 107 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Pha chế dung dịch theo nồng độ yêu cầu
- Bài tập cuối chương 5
- Luyện tập chung trang 108
- Bài 17: Vị trí tương đối của hai đường tròn
- Bài 16: Vị trí tương đối của đường thẳng và đường tròn
- Luyện tập chung trang 96
- Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Bài 14: Cung và dây của một đường tròn
- Bài 13: Mở đầu về đường tròn
- Chương V: Đường tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
