Giải bài 2.12, 2.13, 2.14, 2.15 trang 36 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 36 Kết nối tri thức tập 1. Bài 2.12: Giải các phương trình sau. Bài 2.13: Để loại bỏ x% một loại tảo độc khỏi một hồ nước, người ta ước tính chi phí cần bỏ ra là
Bài 2.12 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các phương trình sau:
a) \(2\left( {x + 1} \right) = \left( {5x - 1} \right)\left( {x + 1} \right);\)
b) \(\left( { - 4x + 3x} \right)x = \left( {2x + 5} \right)x.\)
Phương pháp:
Chú ý cần đưa phương trình đã cho về phương trình dạng \(A\left( x \right).B\left( x \right) = 0\) thì \(A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\)
Lời giải:
a) 2(x + 1) = (5x – 1)(x + 1)
2(x + 1) – (5x – 1)(x + 1) = 0
(x + 1)(2 – 5x + 1) = 0
(x + 1)(3 – 5x) = 0
x + 1 = 0 hoặc 3 – 5x = 0
x = –1 hoặc 5x = 3

b) (–4x + 3)x = (2x + 5)x
(–4x + 3)x – (2x + 5)x = 0
x(–4x + 3 – 2x – 5) = 0
x(–6x – 2) = 0
x = 0 hoặc –6x – 2 = 0
x = 0 hoặc –6x = 2

Bài 2.13 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức
Để loại bỏ x% một loại tảo độc khỏi một hồ nước, người ta ước tính chi phí cần bỏ ra là
\(C\left( x \right) = \frac{{50x}}{{100 - x}}\) (triệu đồng), với \(0 \le x < 100.\)
Nếu bỏ ra 450 triệu đồng, người ta có thể lọai bỏ được bao nhiêu phần trăm loại tảo độc đó?
Phương pháp:
Chi phí bỏ ra là 450 triệu đồng nên ta có \(C\left( x \right) = 450\) từ đó ta có phương trình chứa ẩn ở mẫu, ta giải phương trình đối chiếu điều kiện rồi kết luận bài toán.
Lời giải:
Theo bài, chi phí để loại bỏ tảo độc là C = 450 triệu đồng, nên ta có phương trình: 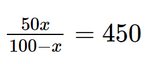
Giải phương trình:
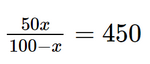
50x = 450.(100 – x)
50x = 45 000 – 450x
50x + 450x = 45 000
500x = 45 000
x = 90.
Giá trị x = 90 thỏa mãn điều kiện 0 ≤ x < 100.
Vậy nếu bỏ ra 450 triệu đồng, người ta có thể loại bỏ được 90% loại tảo độc đó.
Bài 2.14 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các phương trình sau:
a) \(\frac{1}{{x + 2}} - \frac{2}{{{x^2} - 2x + 4}} = \frac{{x - 4}}{{{x^3} + 8}};\)
b) \(\frac{{2x}}{{x - 4}} + \frac{3}{{x + 4}} = \frac{{x - 12}}{{{x^2} - 16}}.\)
Phương pháp:
Các bước giải phương trình chứa ẩn ở mẫu
- Bước 1: Tìm ĐKXĐ
- Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu
- Bước 3: Giải phương trình vừa thu được
- Bước 4: Kết luận (đối chiếu ĐKXĐ).
Lời giải:

Suy ra x2 – 4x = x – 4. (*)
Giải phương trình (*):
x2 – 4x = x – 4
x(x – 4) – (x – 4) = 0
(x – 4)(x – 1) = 0
x – 4 = 0 hoặc x – 1 = 0
x = 4 (thỏa mãn ĐKXĐ) hoặc x = 1 (thỏa mãn ĐKXĐ).
Vậy phương trình đã cho có nghiệm là x = 4 và x = 1.

Suy ra 2x2 + 11x – 12 = x – 12. (*)
Giải phương trình (*):
2x2 + 11x – 12 = x – 12
2x2 + 11x – 12 – x + 12 = 0
2x2 + 10x = 0
2x(x + 5) = 0
2x = 0 hoặc x + 5 = 0
x = 0 (thỏa mãn ĐKXĐ) hoặc x = –5 (thỏa mãn ĐKXĐ).
Vậy phương trình đã cho có nghiệm là x = 0 và x = –5.
Bài 2.15 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức
Cho \(a > b,\) chứng minh rằng:
a) \(4a + 4 > 4b + 3;\)
b) \(1 - 3a < 3 - 3b.\)
Phương pháp:
Áp dụng quy tắc:
- Cộng cả hai vế của bất đẳng thức với một số ta được bất đẳng thức cùng chiều với bất đẳng thức đã cho;
- Nhân cả hai vế của bất đẳng thức với cùng 1 số dương ta được một bất đẳng thức cùng chiều với bất đẳng thức đã cho;
- Nhân cả hai vế của bất đẳng thức với một số âm thì ta được một bất đẳng thức ngược chiều với bất đẳng thức đã cho.
- Áp dụng tính chất bắc cầu \(a < b;b < c\) thì \(a < c\)
Lời giải:
a) Vì a > b nên 4a > 4b, suy ra 4a + 3 > 4b + 3.
Mà 4a + 4 > 4a + 3 nên 4a + 4 > 4b + 3.
Vậy 4a + 4 > 4b + 3.
b) Vì a > b nên –3a < –3b, suy ra 3 – 3a < 3 – 3b.
Mà 1 – 3a < 3 – 3a nên 1 – 3a < 3 – 3b.
Vậy 1 – 3a < 3 – 3b.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 114, 115 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.32, 5.33, 5.34, 5.35, 5.36, 5.37, 5.38, 5.39, 5.40 trang 113 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.28, 5.29, 5.30, 5.31 trang 110 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.24, 5.26, 5.27 trang 107 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Pha chế dung dịch theo nồng độ yêu cầu
- Bài tập cuối chương 5
- Luyện tập chung trang 108
- Bài 17: Vị trí tương đối của hai đường tròn
- Bài 16: Vị trí tương đối của đường thẳng và đường tròn
- Luyện tập chung trang 96
- Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Bài 14: Cung và dây của một đường tròn
- Bài 13: Mở đầu về đường tròn
- Chương V: Đường tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
