Giải bài 3.32, 3.33, 3.34, 3.35, 3.36, 3.37, 3.38, 3.39 trang 65 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 65 Kết nối tri thức tập 1. Bài 3.35: Độ dài đường kính (mét) của hình tròn có diện tích (4,{m^2}) sau khi làm tròn kết quả đến chữ số thập phân thứ hai bằng A. 2,26. Bài 3.36: Một vật rơi tự do từ độ cao 396,9 m. Biết quãng đường chuyển động S (mét) của vật phụ thuộc vào thời gian t (giây) bởi công thức (S = 4,9{t^2}.) Vật chạm đất sau A. 8 giây.
Xem thêm: Bài tập cuối chương 3
Bài 3.32 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Căn bậc hai của 4 là
A. 2.
B. -2.
C. 2 và -2.
D. \(\sqrt 2 \) và \( - \sqrt 2 .\)
Phương pháp:
Căn bậc hai của số A là \(\sqrt A \) và \( - \sqrt A \)
Lời giải:
Đáp án đúng là: C
Ta có 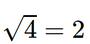 nên căn bậc hai của 4 là 2 và –2.
nên căn bậc hai của 4 là 2 và –2.
Bài 3.33 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Căn bậc hai số học của 49 là
A. 7.
B. -7.
C. 7 và -7.
D. \(\sqrt 7 \) và \( - \sqrt 7 .\)
Phương pháp:
Căn bậc hai của số A là \(\sqrt A \) và \( - \sqrt A \)
Lời giải:
Đáp án đúng là: A
Ta có 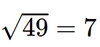 nên căn bậc hai số học của 49 là 7.
nên căn bậc hai số học của 49 là 7.
Bài 3.34 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Rút gọn biểu thức \(\sqrt[3]{{{{\left( {4 - \sqrt {17} } \right)}^3}}}\) ta được
\(\begin{array}{l}A.\,4 + \sqrt {17} .\\B.\,4 - \sqrt {17} .\\C.\,\sqrt {17} - 4.\\D.\, - 4 - \sqrt {17} .\end{array}\)
Phương pháp:
Ta có \(\sqrt[3]{{{A^3}}} = A\)
Lời giải:
Đáp án đúng là: B
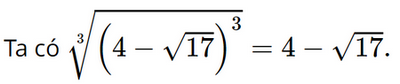
Bài 3.35 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Độ dài đường kính (mét) của hình tròn có diện tích \(4\,{m^2}\) sau khi làm tròn kết quả đến chữ số thập phân thứ hai bằng
A. 2,26. B. 2,50. C. 1,13. D. 1,12.
Phương pháp:
Diện tích hình tròn là \(S = 3,14.{R^2}\)
Lời giải:
Đáp án đúng là: A
Diện tích của hình tròn có bán kính R (m) là πR2 (m2).
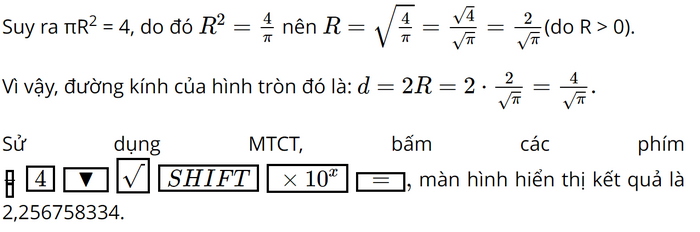
Làm tròn kết quả đến chữ số thập phân thứ hai, ta được: d ≈ 2,26 (m).
Vậy ta chọn phương án A.
Bài 3.36 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Một vật rơi tự do từ độ cao 396,9 m. Biết quãng đường chuyển động S (mét) của vật phụ thuộc vào thời gian t (giây) bởi công thức \(S = 4,9{t^2}.\) Vật chạm đất sau
A. 8 giây.
B. 5 giây.
C. 11 giây.
D. 9 giây.
Phương pháp:
Ta có \(S = 4,9{t^2}\) suy ra \(t = \sqrt {4,9:S} \)
Lời giải:
Đáp án đúng là: D
Quãng đường chuyển động chính là độ cao 396,9 m nên ta có S = 396,9 m.
Suy ra 4,9t2 = 396,9 nên t2 = 81 do đó  (giây) (do t > 0).
(giây) (do t > 0).
Vậy ta chọn phương án D.
Bài 3.37 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Không sử dụng MTCT, tính giá trị của biểu thức \(A = \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {4{{\left( {2 + \sqrt 3 } \right)}^2}} - \frac{1}{{2 - \sqrt 3 }}.\)
Phương pháp:
Ta có \(\sqrt {{A^2}} = \left| A \right|\) và \(\frac{1}{{A - \sqrt B }} = \frac{{A + \sqrt B }}{{\left( {A - \sqrt B } \right)\left( {A + \sqrt B } \right)}} = \frac{{A + \sqrt B }}{{{A^2} - B}}\)
Lời giải:
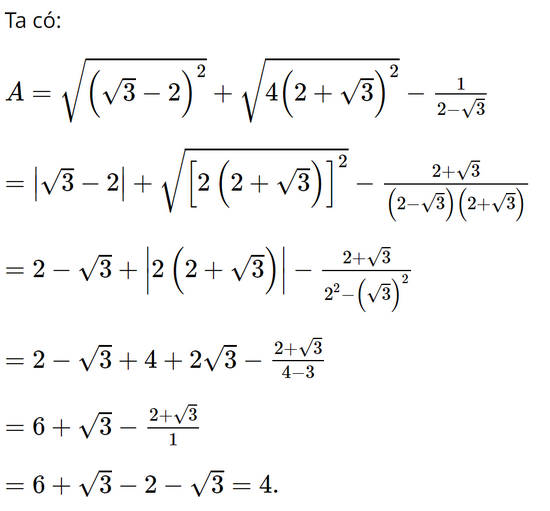
Bài 3.38 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Cho biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x - 2}} - \frac{4}{{\sqrt x + 2}}\left( {x > 0,x \ne 4} \right).\)
a) Rút gọn biểu thức A.
b) Tính giá trị của A tại \(x = 14.\)
Phương pháp:
Để rút gọn biểu thức ta cần quy đồng, mẫu số chung rồi rút gọn như đối với phân thức.
Khi tính giá trị của biểu thức thì ta thay giá trị x cần tính vào biểu thức cần tính, cần kiểm tra điều kiện trước khi thay.
Lời giải:
a) Với x ≥ 0 và x ≠ 4, ta có:

Bài 3.39 trang 65 SGK Toán 9 tập 1 - Kết nối tri thức
Biết rằng nhiệt lượng tỏa ra trên dây dẫn được tính bởi công thức \(Q = {I^2}Rt,\) trong đó Q là nhiệt lượng tính bằng đơn vị Joule (J) , R là điện trở tính bằng đơn vị Ohm (Ω) , I là cường độ dòng điện tính bằng đơn vị Ampe (A) , t là thời gian tính bằng giây (s) . Dòng điện chạy qua một dây dẫn có R = 10 Ω trong thời gian 5 giây.
a) Thay dấu “?” trong bảng sau bằng các giá trị thích hợp.

b) Cường độ dòng điện là bao nhiêu Ampe để nhiệt lượng tỏa ra trên dây dẫn đạt 800 J?
Phương pháp:
a) Thay R = 10 Ω và thời gian 5 giây, và cường độ dòng điện tương ứng ta tính được Q.
b) Từ công thức tính \(Q = {I^2}Rt\) suy ra \(I = \sqrt {Q:Rt} \), thay các giá trị Q, R, t ta tính được I.
Lời giải:
Thay R = 10 (Ω) và thời gian t = 5 (giây) vào công thức Q = I2Rt, ta được:
Q = I2.10.5 = 50I2 (J).
a) Thay I = 1 (A) vào biểu thức trên, ta được: Q = 50.12 = 50 (J).
Thay I = 1,5 (A) vào biểu thức trên, ta được: Q = 50.1,52 = 112,5 (J).
Thay I = 2 (A) vào biểu thức trên, ta được: Q = 50.22 = 200 (J).
Vậy ta hoàn thành được bảng đã cho như sau:

b) Để nhiệt lượng toả ra trên dây dẫn đạt 800 J thì Q = 800 (J)
Suy ra 50I2 = 800.
Do đó I2 = 16 nên 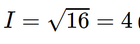 (A) (do I > 0).
(A) (do I > 0).
Vậy cường độ dòng điện là 4 Ampe thì nhiệt lượng toả ra trên dây dẫn đạt 800 J.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 114, 115 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.32, 5.33, 5.34, 5.35, 5.36, 5.37, 5.38, 5.39, 5.40 trang 113 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.28, 5.29, 5.30, 5.31 trang 110 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.24, 5.26, 5.27 trang 107 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Pha chế dung dịch theo nồng độ yêu cầu
- Bài tập cuối chương 5
- Luyện tập chung trang 108
- Bài 17: Vị trí tương đối của hai đường tròn
- Bài 16: Vị trí tương đối của đường thẳng và đường tròn
- Luyện tập chung trang 96
- Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Bài 14: Cung và dây của một đường tròn
- Bài 13: Mở đầu về đường tròn
- Chương V: Đường tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!