Giải bài 4.14, 4.15, 4.16, 4.17, 4.18, 4.19, 4.20 trang 81 SGK Toán 9 Kết nối tri thức tập 1

Bài 4.14 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức

Một cuốn sách khổ \(17 \times 24\) cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi \(\alpha \) là góc giữa đường chéo và cạnh 17 cm. Tính \(\sin \alpha ,\cos \alpha \) (làm tròn đến chữ số thập phân thứ hai)  và tính số đo \(\alpha \) (làm tròn đến độ) .

Phương pháp:

Cuốn sách có dạng hình chữ nhật, để tính tỉ số lượng giác \(\sin \alpha ,\cos \alpha \) liên quan đến đường chéo của hình chữ nhật, ta sử dụng định lý Pytagore để tính.

Chú ý: Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc \(\alpha \), kí hiệu \(\sin \alpha \)

Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \alpha \)

Lời giải:

Ta mô tả cuốn sách khổ 17 × 24 cm như hình vẽ sau:

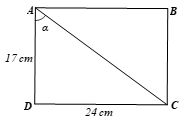
Xét ∆ACD vuông tại D, theo định lí Pythagore, ta có:

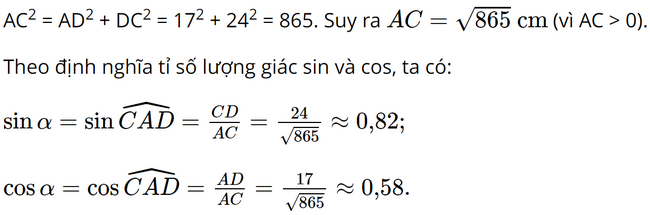
Suy ra α ≈ 55°.

Bài 4.15 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức

Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết \(HB = 3cm,HC = 6cm,\widehat {HAC} = {60^0}.\) Hãy tính độ dài các cạnh (làm tròn đến cm) , số đo các góc của tam giác ABC (làm tròn đến độ) .

Phương pháp:

Ta cần tính các cạnh AB, BC, CA

\(BC = BH + HC\); AC tính dựa vào tỉ số lượng giác của \(\widehat {HAC}\) (\(\sin \widehat {HAC}\) )

Cạnh AB tính thông qua định lý Pythagore trong tam giác vuông ABH, tuy nhiên ta cần tính được cạnh AH, tính cạnh AH thông qua tỉ số lượng giác của \(\widehat {HAC}\left( {\tan \widehat {HAC}} \right)\)

Lời giải:

– Ta có: BC = BH + HC = 3 + 6 = 9 cm.

Xét ∆AHC vuông tại H, ta có:

Bài 4.16 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức

Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m) .

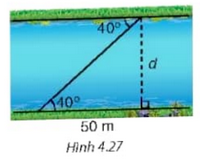
Phương pháp:

Độ dài cạnh góc vuông này bằng cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề

Lời giải:

Vậy chiều rộng của dòng sông là khoảng 42 m.

Bài 4.17 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức

Tính các số liệu còn thiếu (dấu “?”)  ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.

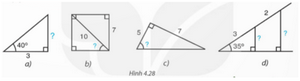
Phương pháp:

Tính cạnh góc vuông này ta lấy cạnh góc vuông kia nhân với tan góc đối hoặc lấy cạnh huyền nhân sin góc đối

Để tính góc trong các hình trên ta sử dụng tỉ số lượng giác sin hoặc tan.

Lời giải:

a) Gọi độ dài cạnh cần tìm là x.

b) Gọi số đo góc cần tìm là α.

Vì tứ giác đã cho có 3 góc vuông nên là hình chữ nhật. Do đó hai cạnh đối nhau có độ dài bằng nhau.

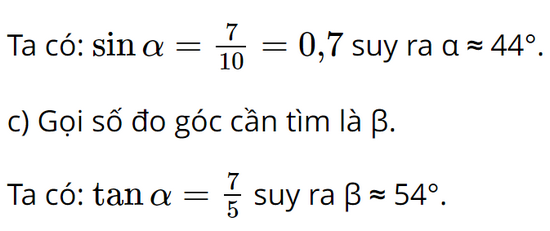
d) Gọi độ dài cạnh góc vuông nhỏ và cạnh góc vuông lớn lần lượt là a, b.

Ta có:

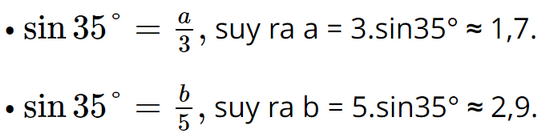
Bài 4.18 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức

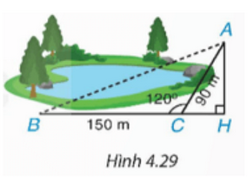
Một bạn muốn tính khoảng cách giữa hai điểm A và B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là \(CA = 90m,CB = 150m\) và \(\widehat {ACB} = {120^0}\) (H.4.29) . Hãy tính AB giúp bạn.

Phương pháp:

Để tính độ dài cạnh AB ta dựa vào tam giác AHB vuông và sử dụng định lý Pythagore để tính, ta cần biết độ dài BH và AH thông qua tam giác ACH, ta tính được góc ACH, rồi sử dụng tỉ số lượng giác của góc ACH.

Lời giải:

Bài 4.19 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức

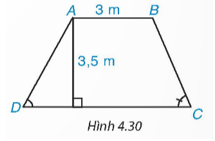
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30) . Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là \(\tan D = 1,25.\) Độ dốc của sườn BC, tức là \(\tan C = 1,5.\) Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).

Phương pháp:

Gọi J là chân đường vuông góc kẻ từ A, ta mới tính được cạnh AD và DJ dựa theo tỉ số lượng giác, chưa đủ để tính cạnh DC và BC, do đó ta kẻ thêm đường cao BK của hình thang, ta sẽ có ABKJ là hình chữ nhật, ta tính được cạnh JK, tam giác BCK tính được BC và CK. Để tính DC ta tổng độ dài 3 cạnh DJ, JK, KC. Chú ý làm tròn đến đơn vị dm tức là phần thập phân lấy 1 chữ số.

Lời giải:

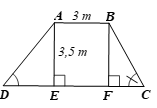
Kẻ AE ⊥ CD, BF ⊥ CD. Khi đó AE // BF.

Vì ABCD là hình thang nên AB // CD, do đó suy ra AB // EF.

Xét tứ giác ABFE có: AE // BF và AB // EF nên là hình bình hành.

Bài 4.20 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức

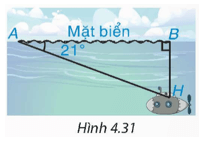
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước một góc \({21^0}\) để lặn xuống (H.4.31) .

a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m) .

b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn)  tàu ở độ sau 200 m (tức là cách mặt nước biển 200 m) ?

Phương pháp:

a) Tàu đi được 200 m tức là độ dài đoạn AH = 200 m, ta cần tính BH theo tỉ số lượng giác (sin A)

b) Tàu ở độ sâu 200 m tức là BH = 200 m cần tính thời gian lặn khi biết vận tốc của tàu, tức là ta phải biết quãng đường tàu đi được AH. Tính AH thông qua tỉ số lượng giác.

Chú ý: Thời gian = quãng đường : vận tốc

Lời giải:

a) Tàu chuyển động theo đường thẳng tạo với mặt nước biển một góc 21° và đi được 200 m tức là AH = 200 m. Độ sâu của tàu so với mặt nước biển là BH.

Xét ∆ABH vuông tại B, ta có:

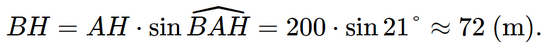
b) Tàu ở độ sâu 200 m tức là BH = 200 m. Quãng đường tàu đi đến độ sâu 200 m là AH.

Xét ∆ABH vuông tại B, ta có:

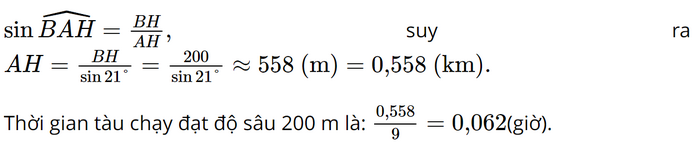
Sachbaitap.com