Giải bài 4.21, 4.22, 4.23, 4.24, 4.25, 4.26, 4.27, 4.28, 4.29, 4.30 trang 81 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 81 Kết nối tri thức tập 1. Bài 4.30: Đố vui. Chu vi Trái Đất bằng bao nhiêu? Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
Bài 4.21 trang 81 SGK Toán 9 tập 1 - Kết nối tri thức
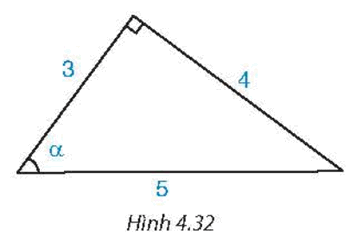
Trong Hình 4.32, \(\cos \alpha \) bằng
A. \(\frac{5}{3}.\)
B. \(\frac{3}{4}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{4}{5}.\)
Phương pháp:
Tỉ số giữa cạnh kề với cạnh huyền là tỉ số lượng giác \(\cos \alpha \)
Lời giải:
Ta có \(\cos \alpha = \frac{3}{5}\) nên đáp án đúng là C.
Bài 4.22 trang 81 SGK Toán 9 tập 1 - Kết nối tri thức
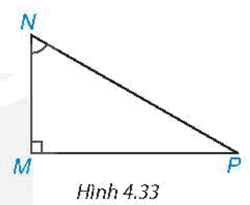
Trong tam giác MNP vuông tại M (H.4.33), \(\sin \widehat {MNP}\) bằng:
A. \(\frac{{PN}}{{MN}}\)
B. \(\frac{{MP}}{{PN}}\)
C. \(\frac{{MN}}{{PN}}\)
D. \(\frac{{MN}}{{MP}}\)
Phương pháp:
Tỉ số giữa cạnh đối và cạnh huyền là \(\sin \alpha \)
Lời giải:
Ta có \(\sin \widehat {MNP} = \frac{{MP}}{{NP}}\). Vậy đáp án đúng là đáp án B.
Bài 4.23 trang 81 SGK Toán 9 tập 1 - Kết nối tri thức
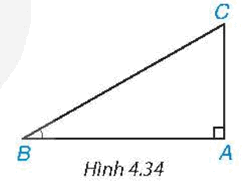
Trong tam giác ABC vuông tại A (H.4.34), \(\tan \widehat B\) bằng
A. \(\frac{{AB}}{{AC}}\).
B. \(\frac{{AC}}{{AB}}\).
C. \(\frac{{AB}}{{BC}}\).
D. \(\frac{{BC}}{{AC}}\).
Phương pháp:
Tỉ số giữa cạnh đối và cạnh kề là \(\tan \alpha \)
Lời giải:
Ta có \(\tan \widehat B = \frac{{AC}}{{AB}}\)
Vậy đáp án đúng là đáp án B.
Bài 4.24 trang 81 SGK Toán 9 tập 1 - Kết nối tri thức
Với mọi góc nhọn \(\alpha \) ta có
A. \(\sin \left( {{{90}^0} - \alpha } \right) = \cos \alpha \)
B. \(\tan \left( {{{90}^0} - \alpha } \right) = \cos \alpha \)
C. \(\cot \left( {{{90}^0} - \alpha } \right) = 1 - \tan \alpha \)
D. \(\cot \left( {{{90}^0} - \alpha } \right) = \sin \alpha \)
Phương pháp:
Hai góc phụ nhau (tổng bằng \({90^0}\)) thì sin bằng cos, tan bằng cot.
Lời giải:
Ta có: \(\sin \left( {{{90}^0} - \alpha } \right) = \cos \alpha \)
Vậy đáp án đúng là đáp án A.
Bài 4.25 trang 81 SGK Toán 9 tập 1 - Kết nối tri thức
Giá trị \(\tan {30^0}\) bằng
A. \(\sqrt 3 \)
B. \(\frac{{\sqrt 3 }}{2}\)
C. \(\frac{1}{{\sqrt 3 }}\)
D. 1
Phương pháp:
Sử dụng MTCT ta có \(\tan {30^0} = \frac{{\sqrt 3 }}{3}\)
Lời giải:
Ta có \(\tan {30^0} = \frac{{\sqrt 3 }}{3}\) nên đáp án đúng là C.
Bài 4.26 trang 81 SGK Toán 9 tập 1 - Kết nối tri thức
Xét các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại. Hỏi các tam giác đó có đồng dạng với nhau không? Tính sin và cos của góc nhọn lớn hơn.
Phương pháp:
Ta xét tam giác ABC vuông, với điều kiện có một góc nhọn bằng hai lần góc nhọn còn lại, ta sẽ tính được số đo của góc B và góc C. Từ đó ta thấy rằng cứ tam giác vuông nào có điều kiện như vậy ta đều tính được góc B và góc C. Do đó ta thấy hai tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại có đồng dạng với nhau. Khi tính được số đo góc, ta sử dụng MTCT để tính kết quả.
Lời giải:
Xét tam giác ABC vuông tại A, có \(\widehat B = 2\widehat C\) mà \(\widehat B + \widehat C = {90^0}\) nên ta có \(2\widehat C + \widehat C = {90^0}\) suy ra \(\widehat C = {30^0}\) do đó \(\widehat B = {60^0}\)
Nên các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại thì sẽ đồng dạng với nhau, do có các góc tương ứng bằng nhau.
\(\sin \widehat B = \sin {60^0} = \frac{{\sqrt 3 }}{2};\cos \widehat B = \cos {60^0} = \frac{1}{2}\)
Bài 4.27 trang 81 SGK Toán 9 tập 1 - Kết nối tri thức
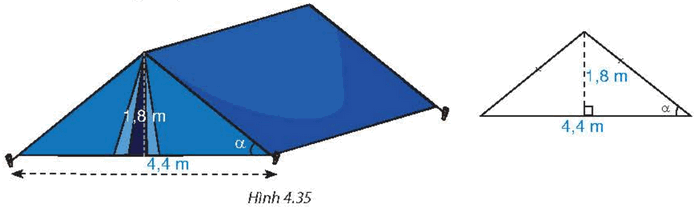
Hình 4.35 là mô hình của một túp lều. Tìm góc \(\alpha \) giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).
Phương pháp:
Ta thấy các cạnh mái lều bằng nhau nên ta có một tam giác cân, đặt tên tam giác rồi ta có thể tính góc thông qua tỉ số lượng giác trong tam giác vuông.
Chú ý: Đường trung tuyến trong tam giác cân vừa là đường cao vừa là đường phân giác.
Lời giải:
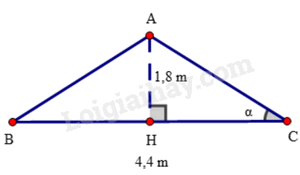
Xét tam giác ABC cân tại A, ta có AH vừa là đường cao vừa là đường trung tuyến nên H là trung điểm của đoạn BC
Do đó \(HB = HC = \frac{{4,4}}{2} = 2,2\) m
Tam giác AHC vuông tại H nên ta có: \(\tan \alpha = \frac{{AH}}{{HC}} = \frac{{1,8}}{{2,2}} = \frac{9}{{11}}\)
Do đó \(\alpha \approx {39^0}17'\)
Bài 4.28 trang 82 SGK Toán 9 tập 1 - Kết nối tri thức
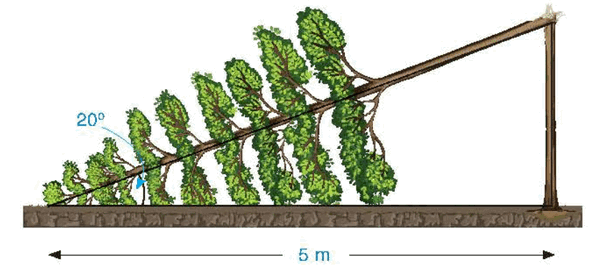
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc \({20^0}\) và chắn ngang lối đi một đoạn 5 m (H.4.36). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Phương pháp:
Để tính chiều cao của cây ta cần tính độ dài của phần cây từ gốc đến điểm gãy và độ dài của phần cây từ điểm gãy đến ngọn cây rồi tính tổng.
Để tính các độ dài trên ta sử dụng tỉ số lượng giác tan và định lý Pythagore.
Lời giải:
Độ dài của phần từ gốc cây đến điểm gãy là \(5.\tan {20^0} \approx 1,8\) m.
Độ dài của phần cây từ điểm gãy đến ngọn cây là \(\sqrt {{5^2} + 1,{8^2}} \approx 5,3\) m.
Trước khi bị gãy, chiều cao của cây khoảng \(1,8 + 5,3 = 7,1\) m.
Bài 4.29 trang 82 SGK Toán 9 tập 1 - Kết nối tri thức
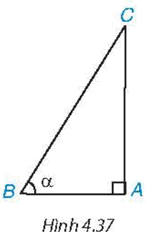
Cho tam giác ABC vuông tại A, có \(\widehat B = \alpha \) (H.4.37).
a) Hãy viết các tỉ số lượng giác \(\sin \alpha ;\cos \alpha \)
b) Sử dụng định lý Pythagore, chứng minh rằng \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Phương pháp:
Tỉ số giữa cạnh đối và cạnh huyền là \(\sin \alpha \)
Tỉ số giữa cạnh kề với cạnh huyền là \(\cos \alpha \)
Định lý Pythagore: cạnh huyền bình phương bằng tổng bình phương của hai cạnh góc vuông.
Lời giải:
a) Ta có \(\sin \alpha = \frac{{AC}}{{BC}};\cos \alpha = \frac{{AB}}{{BC}}\)
b) Tam giác ABC vuông tại A nên ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Nên ta có
\({\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{AC}}} \right)^2} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\) (đpcm).
Bài 4.30 trang 82 SGK Toán 9 tập 1 - Kết nối tri thức
Đố vui. Chu vi Trái Đất bằng bao nhiêu?
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy 1 tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
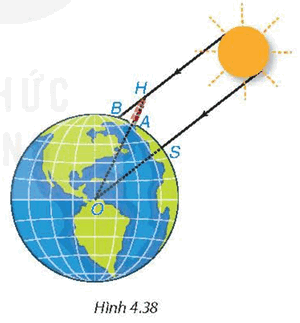
Từ hai quan sát trên, ông có thể tính xấp xỉ “chu vi” của Trái Đất như thế nào? (trên Hình 4.38), điểm O là tâm của Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB.
Phương pháp:
Vẽ hình minh họa để dễ quan sát.
Dựa vào quan sát thứ nhất ta có \(SO \bot SB\) nên \(\Delta SOB\) vuông tại S.
Dựa vào quan sát thứ hai, ta tính được \(\widehat {BHA} \) và chứng minh được BH // OS nên \(\widehat {BHA} = \widehat {AOS}\).
Dựa vào tỉ số lượng giác của các góc để trong tam giác OAS để tính bán kính OA của Trái Đất.
Từ đó sử dụng công thức tính chu vi hình tròn để tính chu vi Trái Đất.
Lời giải:
Ta có hình minh họa các điểm để dễ quan sát như sau:

Qua quan sát thứ nhất, vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng, do đó \(SO \bot SB\) nên \(\Delta SOB\) vuông tại S.
Qua quan sát thứ hai, Eratosthenes thấy 1 tháp cao 25m có bóng trên mặt đất dài 3,1m
Ta có HA là chiều cao của tháp nên HA = 25m, HB là tia sáng mặt trời nên tạo ra bóng của tháp trên mặt đất là AB = 3,1m.
Xét tam giác HBA vuông tại A nên \(\tan \widehat {BHA} = \frac{{BA}}{{HA}} = \frac{{3,1}}{{25}} = 0,124\), suy ra \(\widehat {BHA} \approx 7^04'\).
Mà các tia nắng mặt trời chiếu cùng một góc và cùng 1 thời điểm trong ngày nên các tia sáng BH và OS song song với nhau (BH // OS).
Khi đó ta có: \(\widehat {BHA} = \widehat {AOS}\) (hai góc so le trong). Do đó \(\widehat {AOS} \approx 7^0 4'\).
Ta có khoảng cách của thành phố Alexandria và Syene là 800km nên AS = 800km.
Xét tam giác OAS vuông tại S nên ta có:
\(\sin \widehat {AOS} = \frac{{AS}}{{OA}}\) suy ra \(OA = \frac{{AS}}{{\sin \widehat {AOS}}} \approx \frac{{800}}{{\sin 7^0 4'}} \approx 6503\left( {km} \right)\)
Vì OA là bán kính Trái Đất nên ta tính được chu vi Trái Đất là:
\(C = 2\pi .OA \approx 2.3,14 .6503 \approx 40839\left( {km} \right)\)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 114, 115 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.32, 5.33, 5.34, 5.35, 5.36, 5.37, 5.38, 5.39, 5.40 trang 113 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.28, 5.29, 5.30, 5.31 trang 110 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.24, 5.26, 5.27 trang 107 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Pha chế dung dịch theo nồng độ yêu cầu
- Bài tập cuối chương 5
- Luyện tập chung trang 108
- Bài 17: Vị trí tương đối của hai đường tròn
- Bài 16: Vị trí tương đối của đường thẳng và đường tròn
- Luyện tập chung trang 96
- Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Bài 14: Cung và dây của một đường tròn
- Bài 13: Mở đầu về đường tròn
- Chương V: Đường tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!