Giải bài 5.14, 5.15, 5.16, 5.17, 5.18, 5.19 trang 96 SGK Toán 9 Kết nối tri thức tập 1

Bài 5.14 trang 97 SGK Toán 9 tập 1 - Kết nối tri thức

Cho dây AB không qua tâm của đường tròn (O). Gọi A’ và B’ là hai điểm lần lượt đối xứng với A và B qua (O). Hỏi đường trung trực của A’B’ có phải là trục đối xứng của (O) hay không? Tại sao? 

Phương pháp:

Chứng minh đường trung trực của A’B’ đi qua tâm O.

Lời giải:

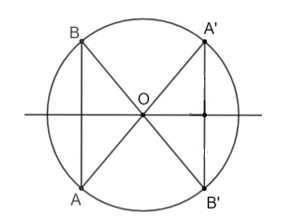
Vì A' và B' là hai điểm lần lượt đối xứng với A và B qua (O) nên OA = OA', OB = OB'.

Mà dây AB không qua tâm của đường tròn (O) nên OA = OB (đều là bán kính của đường tròn (O)).

Suy ra OA = OA' = OB = OB'.

Do đó, O thuộc đường trung trực của A'B'.

Vậy đường trung trực của A'B' là một trục đối xứng của (O).

Bài 5.15 trang 97 SGK Toán 9 tập 1 - Kết nối tri thức

Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:

a) Đường tròn đường kính BC đi qua các điểm H và K;

b) KH < BC.

Phương pháp:

Trong đường tròn, đường kính là dây lớn nhất

Tam giác vuông có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền

Lời giải:

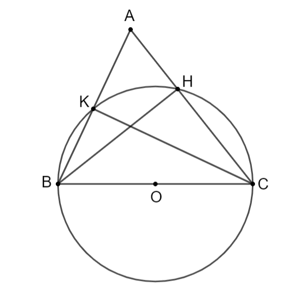
a) Gọi trung điểm của BC là O.

Tam giác vuông BKC có KO là đường trung tuyến KO ứng với cạnh huyền BC nên

KO = OB = OC hay B, K, C thuộc đường tròn tâm O đường kính BC.          (1)

Tam giác BHC vuông tại H có HO là đường trung tuyến ứng với cạnh huyền BC nên

HO = BO = OB hay B, H, C thuộc được đường tròn tâm O đường kính BC.   (2)

Từ (1) và (2) ta có K, H thuộc đường tròn tâm O đường kính BC.

Vậy đường tròn đường kính BC đi qua các điểm H và K.

b) Đường tròn tâm O có BC là đường kính và KH là dây không qua tâm O.

Do đó KH < BC.

Bài 5.16 trang 97 SGK Toán 9 tập 1 - Kết nối tri thức

Có thể xem guồng nước (còn gọi là cọn nước) là một công cụ hay cỗ máy có dạng hình tròn, quay được nhờ sức nước chảy (H.5.22a). Guồng nước thường thấy ở các vùng miền núi. Nhiều guồng nước được làm bằng tre, dùng để đưa nước lên ruộng cao, giã gạo hoặc làm một số việc khác.

Giả sử ngấn nước ngăn cách giữa phần trên và phần dưới của một guồng nước được biểu thị bởi cung ứng với một dây dài 4 m và điểm ngập sâu nhất là 0,5 m (trên hình 5.22b, điểm ngập sâu nhất là điểm C, ta có AB = 4 m và HC = 0, 5 m). Dựa vào đó, em hãy tính bán kính của guồng nước.

Phương pháp:

Theo bài 5.6, \(\widehat {HOA} = \frac{{\widehat {AOB}}}{2} = \frac{{100^\circ }}{2} = 50^\circ \). Xét tam giác OAH vuông tại H từ đó tính được độ dài bán kính OA.

Lời giải:

Tam giác OAB có OA = OB nên tam giác OAB cân tại O.

Mà OH là đường cao nên OH cũng là đường trung trực của AB hay H là trung điểm của AB.

Do đó AH = HB = 1/2 AB = 1/2 . 4 = 2 (m)

Xét đường tròn tâm O bán kính R nên ta có

OH = OC – HC = R − 0,5 (m).

Tam giác OAH vuông tại H nên ta có:

OA² = OH² + AH² (theo định lí Pythagore)

Thay số ta có: R² = (R − 0,5)² + 4²

Hay R² = R² – R + 0,25 + 16 suy ra R = 16,25 m.

Vậy bán kính của guồng nước là 16,25 m.

Bài 5.17 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức

Cho đường tròn (O; 5 cm).

a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5 cm.

b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm).

c) Tính số đo và độ dài của cung nhỏ AB.

d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.

Phương pháp:

a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm. Kẻ đoạn thẳng AB vuông góc với OH tại H.

b) Ta chứng minh \(AH = BH\)\( \Rightarrow AB = 2AH\). Áp dụng định lý Pythagore để tính AH, từ đó suy ra độ dài AB.

c) Tính \(\sin \widehat {AOH}\) suy ra \(\widehat {AOH}\)và sđ\(\overset\frown{AB}\), từ đó tính được độ dài cung \(\overset\frown{AB}\).

d) Áp dụng công thức tính diện tích hình quạt tròn.

Lời giải:

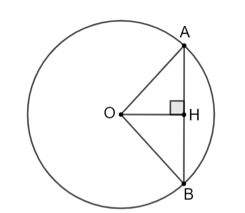
a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm.

Kẻ đoạn thẳng AB vuông góc với OH tại H, cắt đường tròn tại A và B ta được dây cung AB cần vẽ.

b) Gọi H là trung điểm của AB.

Xét ΔOAH và ΔOBH có

OA = OB = R

Cạnh OH chung

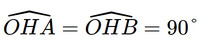
Do đó ΔOAH = ΔOBH (cạnh huyền – cạnh góc vuông).

Suy ra AH = BH (hai cạnh tương ứng).

Nên AB = 2AH.

Xét tam giác OAH vuông tại H có:

AH² + OH² = OA² (định lý Pythagore)

Hay AH² = OA² – OH² = 5² − 2,5² = 18,75.

Bài 5.18 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức

Ba bộ phận truyền chuyển động của một chiếc xe đạp gồm một giò đĩa (bánh răng gắn với bàn đạp), một chiếc líp (cũng có dạng bánh răng) gắn với bánh xe và bộ xích (H.5.23). Biết rằng giò đĩa có bán kính 15 cm, líp có bán kính 4 cm và bánh xe có đường kính 65 cm. Hỏi khi người đi xe đạp một vòng thì xe chạy được quãng đường dài bao nhiêu mét (làm tròn kết quả đến hàng phần chục)?

Phương pháp:

Bán kính tỉ lệ nghịch với số vòng quay được của líp và giò đĩa.

Ta tính số vòng líp quay được khi đạp một vòng xe sau đó đem nhân với chu vi bánh xe.

Lời giải:

Bán kính tỉ lệ nghịch với số vòng quay được của líp và giò đĩa.

Khi đạp 1 vòng thì bánh xe (hoặc líp) quay được số vòng là:

15 : 4 = 15/4 (vòng)

Chu vi một vòng bánh xe là: 2 . π . 4 = 8π (cm)

Khi người đi xe đạp một còng thì xe chạy được quãng đường là:

8π . 15/4 = 30π (cm) = 3/10 π (m) ≈ 0,9 (m).

Vậy khi người đi xe đạp một vòng thì xe chạy được quãng đường dài khoảng 0,9 mét.

Bài 5.19 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức

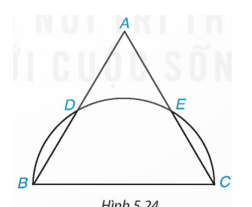
Cho tam giác đều ABC có AB = \({\rm{2}}\sqrt 3 \)cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24).

a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy.

b) Tính diện tích của hình viên phân (xem ví dụ 2) giới hạn bởi dây BD và cung nhỏ BD.

Phương pháp:

a) Chứng mình tam giác OBD đều, từ đó suy ra \(\widehat {{\rm{BOD}}} = 60^\circ \). Tương tự có: \(\widehat {{\rm{BOD}}} = \widehat {{\rm{COE}}} = \widehat {{\rm{DOE}}} = 60^\circ \) hay số đo các cung nhỏ BD, DE và EC bằng nhau.

b) Áp dụng công thức tính diện tích hình viên phân: \(S = {R^2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)\)

Lời giải:

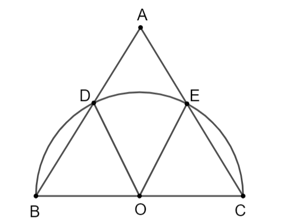
a) Gọi O là trung điểm của BC.

Vì OB = OD nên tam giác OBD là tam giác cân.

Diện tích hình viên phân giới hạn bởi dây BD và cung nhỏ BD là:

Sachbaitap.com