Giải bài 7.41, 7.42, 7.43, 7.44, 7.45, 7.46, 7.47, 7.48, 7.49, 7.50 trang 57, 58 SGK Toán 8 Kết nối tri thức tập 2

Bài 7.41 trang 57 SGK Toán 8 tập 2 - Kết nối tri thức

Phương trình nào sau đây là phương trình bậc nhất một ẩn 

A. 0x+2=0

B. 2x+1=2x+2

C.\(2{{\rm{x}}^2}\)+1=0

D. 3x−1=0

Phương pháp:

Phương trình nào có dạng \(y = {\rm{ax  +  b(a}} \ne {\rm{0)}}\)là phương trình bậc nhất một ẩn

Lời giải:

Đáp án đúng là: D

Phương trình 3x – 1 = 0 là phương trình bậc nhất một ẩn vì a ≠ 0 và bậc của phương trình là 1.

Bài 7.42 trang 57 SGK Toán 8 tập 2 - Kết nối tri thức

Tập nghiệm S của phương trình 3(x+1)−(x−2)=7−2x là

A. S=0                               B. S={\(\frac{1}{2}\)}

C.S=∅                                D. S=R

Phương pháp:

Giải phương trình đã cho và viết tập nghiệm từ đó chọn được đáp án đúng

Lời giải:

Đáp án đúng là: B

3(x + 1) – (x – 2) = 7 – 2x

3x + 3 – x + 2 = 7 – 2x

4x = 2

x =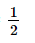 

Vậy tập nghiệm của phương trình là S =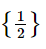 

Bài 7.43 trang 57 SGK Toán 8 tập 2 - Kết nối tri thức

Hàm số nào nào sau đây là hàm số bậc nhất?

A. y=0x+3

B. y= \(3{{\rm{x}}^2}\)+2

C. y=2x

D. y=0

Phương pháp:

Hàm số  nào có dạng \(y = {\rm{ax  +  b(a}} \ne {\rm{0)}}\)là hàm số bậc nhất một ẩn

Lời giải:

Đáp án đúng là: C

Hàm số y = 2x là hàm số bậc nhất một ẩn vì a ≠ 0 và bậc của phương trình là 1.

Bài 7.44 trang 57 SGK Toán 8 tập 2 - Kết nối tri thức

Đường thẳng có hệ số góc bằng 2 và đi qua điểm (-1;2) là:

A. y=2x+2

B.y=2x−1

C. y=−x+2

D. y=2x+4

Phương pháp:

Vì hàm số có hệ số góc là 2 => y=2x+b

Thay x = -1; y = 2 vào công thức hàm số để tìm ra b

Suy ra được hàm số cần tìm 

Lời giải:

Đáp án đúng là: D

Vì đường thẳng có hệ số góc là 2 nên đường thẳng này có dạng y = 2x + b.

Lại có đường thẳng đi qua điểm (–1; 2), thay x = –1; y = 2 vào y = 2x + b ta được

2 = 2 . (– 1) + b, suy ra b = 4.

Vậy ta có đường thẳng cần tìm là y = 2x + 4.

Bài 7.45 trang 57 SGK Toán 8 tập 2 - Kết nối tri thức

Giá trị m để đường thẳng y=(m+1)x+2 song song với đường thẳng y=−2x là 

A. m=−3

B. m=−2

C. m=2

D. m=1

Phương pháp:

Vận dụng hệ số góc của hai đường thẳng song song

Lời giải:

Đáp án đúng là: A

Hai đường thẳng đã cho song song với nhau khi m + 1 = –2, tức là m = –3.

Bài 7.46 trang 57 SGK Toán 8 tập 2 - Kết nối tri thức

Giải các phương trình sau:

a) 5(x−1)−(6−2x)=8x−3

b) \(\frac{{2{\rm{x}} - 1}}{3} - \frac{{5 - 3{\rm{x}}}}{2} = \frac{{x + 7}}{4}\)

Phương pháp:

Đưa các phương trình đã cho về dạng phương trình bậc nhất một ẩn rồi giải

Lời giải:

a) 5(x – 1) – (6 – 2x) = 8x – 3

5x + 2x – 8x = 6 + 5 – 3

–x = 8

x = –8.

Vậy phương trình có tập nghiệm S = {–8}.

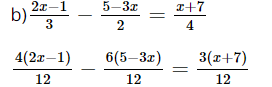
8x – 4 – 30 + 18x = 3x + 21

8x + 18x – 3x = 21 + 4 + 30

23x = 55

x =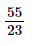 

Vậy phương trình có tập nghiệm S =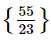 

Bài 7.47 trang 57 SGK Toán 8 tập 2 - Kết nối tri thức

Số tiền thuế thu nhập cá nhân khi mức thu nhập chịu thuế trong năm trong khoảng từ trên 60 triệu đồng đến 120 triệu đồng được cho bởi công thức sau:

                 T(x)=0,1x−3 (triệu đồng)

trong đó 60<x≤120 (triệu đồng) là mức thu nhập chịu thuế của người đó trong năm. 

a) Tính số thuế thu nhập phải đóng khi mức thu nhập chịu thuế trong năm là 100 triệu đồng

b) Nếu một người phải đóng 8 triệu đồng tiền thuế thu nhập cá nhân thì mức thu nhập chịu thuế của người đó trong năm là bao nhiêu, biết rằng người đó có thu nhập chịu thuế trong khoảng từ trên 60 triệu đồng đến 120 triệu đồng

Phương pháp:

a) Thay x = 100 vào T(x) để tính số thuế thu nhập phải đóng khi mức thu nhập chịu thuế của ngườu đó là 100 triệu đồng.

b) Cho T(x) = 8 tìm ra x là mức thu nhập chịu thuế của người đó trong năm.

Lời giải:

a) Số thuế thu nhập phải đóng khi mức thu nhập chịu thuế trong năm là 100 triệu đồng: 

T(100) = 0,1 . 100 – 3 = 7 (triệu đồng).

b) Nếu một người phải đóng 8 triệu đồng tiền thuế thu nhập cá nhân nghĩa là T(x) = 8, tức là 0,1x – 3 = 8, suy ra x = 110 (thỏa mãn điều kiện của đề bài).

Vậy người đó có thu nhập chịu thuế là 110 triệu đồng.

Bài 7.48 trang 58 SGK Toán 8 tập 2 - Kết nối tri thức

Một cửa hàng sách giảm giá 20% cho một cuốn sách. Vì là khách quen của cửa hàng nên bạn An được giảm thêm 10% trên giá đã giảm, do đó chỉ phải trả 36 000 đồng cho cuốn sách đó. Hỏi giá ban đầu của cuốn sách đó nếu không giảm giá là bao nhiêu?

Phương pháp:

Gọi giá ban đầu của cuốn sách là x.

Viết phương trình giá tiền mới của sách là 36 000 đồng từ đó tìm ra giá ban đầu của cuốn sách.

Lời giải:

Bài 7.49 trang 58 SGK Toán 8 tập 2 - Kết nối tri thức

Hai ô tô cùng xuất phát từ Hà Nội đi Hạ Long lúc 8 giờ sáng, trên cùng một tuyến đường. Vận tốc của một ô tô lớn hơn 5km/h so với ô tô kia. Xe đi nhanh hơn đến Hạ Long lúc 10h45 phút sáng, trước xe kia 15 phút. Hỏi vận tốc của mỗi ô tô là bao nhiêu? Tính độ dài quãng đường từ Hà Nội đến Hạ Long 

Phương pháp:

Gọi vận tốc ô tô đi chậm hơn là x (km/h)

Từ đó viết phương trình, giải phương trình và tìm được độ dài quãng đường từ Hà Nội đến Hạ Long

Lời giải:

Thời gian di chuyển của ô tô đi nhanh hơn là: 

10 giờ 45 phút – 8 giờ = 2 giờ 45 phút = 2,75 giờ.

Ta có 15 phút = 0,25 giờ.

Gọi vận tốc ô tô đi chậm hơn là x (km/h). Điều kiện x > 0.

Vận tốc của ô tô đi nhanh hơn là: x + 5 (km/h).

Quãng đường di chuyển của ô tô đi nhanh hơn là: 2,75(x + 5) (km).

Quãng đường di chuyển của ô tô đi chậm hơn là: 3x (km).

Vì quãng đường hai xe đi được là như nhau nên ta có phương trình

2,75(x + 5) = 3x

Giải phương trình trên như sau:

2,75(x + 5) = 3x

2,75x + 13,75 = 3x

3x – 2,75x = 13,75

0,25x = 13,75

x = 55 (thỏa mãn điều kiện).

Vận tốc của ô tô đi chậm hơn là 55 km/h.

Vận tốc của ô tô đi nhanh hơn là 55 + 5 = 60 (km/h).

Quãng đường từ Hà Nội đến Hạ Long dài 3 . 55 = 165 km.

Bài 7.50 trang 58 SGK Toán 8 tập 2 - Kết nối tri thức

Cho hàm số bậc nhất y=(m+2)x+3

a) Tìm m để đồ thị hàm số song song với đường thẳng y=−x

b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a

c) Tìm giao điểm A của đồ thị hàm số tìm được ở câu a và đồ thị của hàm số y=x+1. Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số y=x+1 với trục Ox

Phương pháp:

b,  Xác định hai điểm thuộc mỗi đồ thị rồi vẽ đồ thị hàm số.

c) Xác định tọa độ các điểm A, B. Tính AB, OA, OB.

Gọi H là chân đường vuông góc hạ tử A xuống trục hoành.

Tính diện tích tam giác OAB = \(\frac{1}{2}\)AH.OB.

Lời giải:

Hàm số y = (m + 2)x + 3 là hàm số bậc nhất khi m + 2 ≠ 0, hay m ≠ – 2.

Vậy ta có điều kiện m ≠ – 2.

a) Đồ thị hàm số đã cho song song với đường thẳng y = –x khi m + 2 = –1, tức là m = –3.

Giá trị này thỏa mãn điều kiện m ≠ – 2.

Vậy giá trị m cần tìm là m = –3.

b) Với m =  –3 ta có hàm số y = –x + 3.

Đồ thị hàm số y = –x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0).

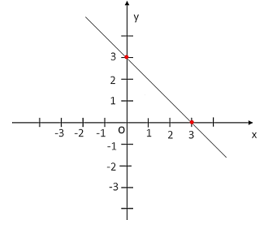
c) Phương trình hoành độ giao điểm của hai đồ thị hàm số y = –x + 3 và y = x + 1 là

– x + 3 = x + 1.

Giải phương trình trên ta được x = 1.

Từ đó suy ra y = 1 + 1 = 2.

Vậy giao điểm của hai đồ thị hàm số cần tìm là A(1; 2).

Giao điểm của đồ thị hàm số y = x + 1 với trục hoành Ox là B(–1; 0). Do đó OB = 1.

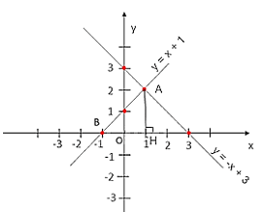
Gọi H là chân đường vuông góc hạ từ A xuống trục hoành. Khi đó AH là đường cao của tam giác OAB.

Ta thấy H(1; 0) và AH = |yA| = 2.

Diện tích tam giác OAB là SOAB = 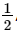AH . OB = . 2 . 1 = 1 (đơn vị diện tích).

Sachbaitap.com