Giải bài 7.7, 7.8, 7.8, 7.9, 7.10, 7.11 trang 35,36 SGK Toán 8 Kết nối tri thức tập 2

Bài 7.7 trang 35 SGK Toán 8 tập 2 - Kết nối tri thức

Chị Linh làm việc trong một ngân hàng và được thưởng Tết bằng 2,5 tháng lương. Tổng thu nhập một năm của chị Linh bao gồm lương 12 tháng và thưởng Tết là 290 triệu đồng. Hỏi lương hằng tháng của chị Linh là bao nhiêu 

Phương pháp:

Gọi x (triệu đồng) là lương hằng tháng của chị Linh  (0<x<290)

Từ đó, viết phương trình, giải phương trình và tìm ra lương hàng tháng của chị Linh

Lời giải:

Gọi x (triệu đồng) là lương hàng tháng của chị Linh (0 < x < 290).

Khi đó, thưởng Tết của chị Linh là 2,5x (triệu đồng).

Lương 12 tháng của chị Linh là 12x (triệu đồng).

                                                14,5x = 290

                                                x = 20 (thỏa mãn).

Vậy lương hàng tháng của chị Linh là 20 triệu đồng.

Bài 7.8 trang 35 SGK Toán 8 tập 2 - Kết nối tri thức

Bác Hưng đầu tư 300 triệu đồng vào hai khoản: mua trái phiếu doanh nghiệp với lãi suất 8% một năm và gửi tiết kiệm ngân hàng với lãi suất 6% một năm. Cuối năm bác Hưng nhận được 22 triệu đồng tiền lãi. Hỏi bác Hưng đã đầu tư vào mỗi khoản bao nhiêu tiền?

Phương pháp:

Gọi số tiền bác Hưng dùng để mua trái phiếu doanh nghiệp là x (triệu đồng)

Từ đó, viết phương trình, giải phương trình và tìm ra số tiền bác Hưng đầu tư vào mỗi khoản là bao nhiêu.

Lời giải:

Gọi số tiền bác Hưng dùng để mua trái phiếu doanh nghiệp là x (triệu đồng).

Điều kiện: 0 ≤ x ≤ 300.

Khi đó số tiền bác Hưng dùng để gửi tiết kiệm ngân hàng là 300 – x (triệu đồng).

Theo đề bài ta có phương trình: 0,08x + 0,06(300 – x) = 22

                                                0,08x + 18 – 0,06x = 22

                                                0,02x = 4

                                                x = 200 (thỏa mãn)

Vậy bác Hưng dùng 200 triệu để mua trái phiếu và dùng 100 triệu để gửi tiết kiệm ngân hàng.

Bài 7.9 trang 36 SGK Toán 8 tập 2 - Kết nối tri thức

Nhân dịp khai trương, một siêu thị điện máy đã giảm giá nhiều mặt hàng để thu hút khách hàng. Tổng giá niêm yết của một chiếc ti vi loại A và một chiếc tủ lạnh loại B là 36.8 triệu đồng. Trong dịp này tivi loại A được giảm 30% và tủ lạnh loại B được giảm 25% nên bác Cường đã mua một chiếc tivi và một chiếc tủ lạnh nói trên với tổng số tiền là 26,805 triệu đồng. Hỏi giá niêm yết của một chiếc tivi loại A và mỗi chiếc tủ lạnh loại B là bao nhiêu ?

Phương pháp:

Gọi giá của chiếc ti vi loại A là x ( 0<x<36,8)

Từ đó ta tìm các dữ liệu liên quan, viết phương trình và giải phương trình để tìm ra giá niêm yết của một chiếc ti vi loại A và loại B là bao nhiêu tiền

Lời giải:

Gọi x (triệu đồng) là giá niêm yết của mỗi chiếc ti vi loại A. Điều kiện 0 < x < 36,8.

Khi đó, giá niêm yết của mỗi chiếc tủ lạnh loại B là 36,8 – x (triệu đồng).

Vì ti vi loại A được giảm 30% nên giá bán của mỗi chiếc ti vi loại A sau khi giảm giá là 0,7x (triệu đồng).

Tương tự, vì tủ lạnh loại B được giảm giá 25% nên giá bán của mỗi chiếc tủ lạnh loại B sau khi giảm giá là 0,75(36,8 – x) (triệu đồng).

Theo đề bài ta có phương trình: 0,7x + 0,75(36,8 – x) = 26,805

                                                0,7x + 27,6 – 0,75x = 26,805

                                                –0,05x = 26,805 – 27,6

                                                x = 15,9 (thỏa mãn)

Vậy giá niêm yết của mỗi chiếc ti vi loại A là 15,9 triệu đồng, giá niêm yết của mỗi chiếc tủ lạnh loại B là 36,8 – 15,9 = 20,9 triệu đồng.

Bài 7.10 trang 36 SGK Toán 8 tập 2 - Kết nối tri thức

Bạn Nam đi xe đạp rời nhà lúc 14 giờ với vận tốc 12km/h. Khi Hùng đến nhà Nam vào lúc 14 giờ 10 phút thì mẹ Nam chỉ hướng đường đi của Nam cho Hùng và Hùng đi xe đạp đuổi theo với vận tốc 18km/h, Hỏi đến lúc mấy giờ thì Hùng đuổi kịp Nam 

Phương pháp:

Gọi thời gian di chuyển của Nam là: x(giờ) (x>0)

Từ đó, viết phương trình và giải phương trình, tính được lúc mấy giờ thì Hùng đuổi kịp Nam

Lời giải:

Gọi thời gian di chuyển của Nam là x (giờ) (x > 0).

Khi đó, quãng đường Nam đi được là 12x (km).

Nam rời nhà lúc 14 giờ và Hùng đến nhà Nam lúc 14 giờ 10 phút nên Hùng di chuyển để đuổi kịp Nam sau Nam 10 phút, tức là 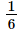 giờ.

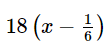 Thời gian di chuyển của Hùng là(giờ).

Quãng đường Hùng đi được là 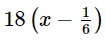 (km).

Theo đề bài, ta có phương trình: 

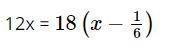
18x – 12x = 3

6x = 3

x = 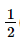(thỏa mãn).

Ta có 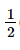giờ = 30 phút.                                         

Vậy Hùng đuổi kịp Nam lúc 14 giờ 30 phút.

Bài 7.10 trang 36 SGK Toán 8 tập 2 - Kết nối tri thức

Hai công ty viễn thông đưa ra hai gói cước cho điện thoại cố định như sau

a) Gọi x là số phút gọi trong tháng. Hãy biểu thị theo x, số tiền phải trả trong tháng (tính theo nghìn đồng) khi sử dụng mỗi gói cước nói trên.

b) Hỏi với bao nhiêu phút gọi thì số tiền phải trả trong tháng khi sử dụng dịch vụ của hai công ty viễn thông này là như nhau 

Phương pháp:

Số tiền phải trả trong tháng khi sử dụng gói cước của công ty A là: 0,9x+32 (nghìn đồng)

Số tiền phải trả trong tháng khi sử dụng gói cước của công ty B là: 0,7x+38 (nghìn đồng)

Tù đó viết phương trình, giải phương trình, tìm ra số phút gọi để số tiền phải trả trong tháng khi sử dụng dịch vụ của hai công ty viễn thông này là như nhau 

Lời giải:

a) Ta có 900 đồng = 0,9 nghìn đồng; 700 đồng = 0,7 nghìn đồng.

Số tiền phải trả trong tháng khi sử dụng gói cước của công ty A là 

32 + 0,9x (nghìn đồng).

Số tiền phải trả trong tháng khi sử dụng gói cước của công ty B là

38 + 0,7x (nghìn đồng).

b) Theo đề bài, ta có phương trình: 

32 + 0,9x = 38 + 0,7x

 0,2x = 6

 x = 30.

Vậy với 30 phút gọi thì số tiền phải trả trong tháng khi sử dụng dịch vụ của hai công ty viễn thông này là như nhau.

Sachbaitap.com