Giải bài 9.37, 9.38, 9.39, 9.40, 9.41, 9.42, 9.43, 9.44, 9.45, 9.46, 9.47, 9.48 trang 110, 110 SGK Toán 8 Kết nối tri thức tập 2
Giải sách giáo khoa Toán lớp 8 trang 110, 110 Kết nối tri thức với cuộc sống tập 2: bài 9.37, 9.38, 9.39, 9.40, 9.41, 9.42, 9.43, 9.44, 9.45, 9.46, 9.47, 9.48. Cho tam giác ABC vuông tại A có AB=5cm, AC=4cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB. Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng
Xem thêm: Bài tập cuối chương 9
Bài 9.37 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức
Cho ABC là tam giác không cân. Biết ΔA′B′C′ ∽ ΔABC. Khẳng định nào sau đây là đúng?
A. ΔA′C′B′ ∽ ΔACB
B. ΔB′C′A′ ∽ ΔBAC
C. ΔB′A′C′ ∽ ΔBCA
D. ΔA′C′B′ ∽ ΔABC
Phương pháp:
Dựa vào định nghĩa tam giác đồng dạng
Lời giải:
Đáp án đúng là A
Vì ΔA′B′C′ ∽ ΔABC nên đỉnh A' tương ứng với đỉnh A, đỉnh B' tương ứng với đỉnh B, đỉnh C' tương ứng với đỉnh C. Vậy xét các đáp án ta thấy khẳng định A là khẳng định đúng do các cặp đỉnh tương ứng với nhau theo thứ tự trên.
Bài 9.38 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức
Cho ΔA′B′C′ ∽ ΔABC với tỉ số đồng dạng bằng 2. Khẳng định nào sau đây là đúng:
A. \(\frac{{AB}}{{A'B'}} = 2\)
B. \(\frac{{AB}}{{A'C'}} = 2\)
C. \(\frac{{A'B'}}{{AB}} = 2\)
D. \(\frac{{A'B'}}{{AC}} = 2\)
Phương pháp:
Sử dụng tam giác đồng dạng để suy ra các tỉ số đồng dạng
Lời giải:
Đáp án đúng là C
Vì ΔA′B′C′ ∽ ΔABC, suy ra 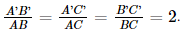
Bài 9.39 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức
Trong các bộ ba số đo dưới đây, đâu là số đo ba cạnh của một tam giác vuông?
A. 3 m; 5 m; 6 m
B. 6 m; 8 m; 10 m
C. 1 cm; 0,5 cm; 1,25 cm
D. 9 m; 16 m; 25 m.
Phương pháp:
Áp dụng định lí Pythagore
Lời giải:
Đáp án đúng là B
Xét đáp án B ta thấy 62 + 82 = 102 (= 100) nên bộ ba này tạo thành tam giác vuông.
(theo định lí Pythagore đảo).
Bài 9.40 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF
A. \(\widehat B = \widehat E\)
B. \(\widehat C = \widehat F\)
C. \(\widehat B + \widehat C = \widehat E + \widehat F\)
D. \(\widehat B - \widehat C = \widehat E - \widehat F\)
Phương pháp:
Sử dụng ΔABC ∽ ΔDEF suy ra các góc tương ứng bằng nhau.
Lời giải:
Đáp án đúng là C
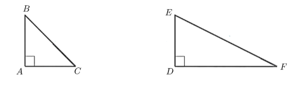
Xét từng đáp án:
+ Hai tam giác ABC vuông ở A và DEF vuông ở D có 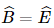 thì ΔABC ∽ ΔDEF.
thì ΔABC ∽ ΔDEF.
+ Hai tam giác ABC vuông ở A và DEF vuông ở D có 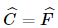 thì ΔABC ∽ ΔDEF.
thì ΔABC ∽ ΔDEF.
Do đó, dữ kiện ở hai đáp án A và B suy ra ΔABC ∽ ΔDEF.
+ Xét đáp án D: Vì tam giác ABC vuông ở A nên 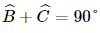 ;
;
Tam giác DEF vuông ở D nên 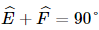 .
.
Do đó, B^+C^=E^+F^">ˆ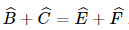 .
.
Mà ta có 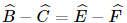 .
.
Cộng vế theo vế ta được 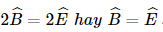 . Khi đó ΔABC ∽ ΔDEF.
. Khi đó ΔABC ∽ ΔDEF.
+ Dữ kiện ở đáp án C luôn xảy ra với mọi cặp tam giác vuông nên từ dữ kiện này không suy ra được ΔABC ∽ ΔDEF.
Bài 9.41 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức
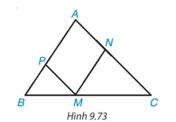
Cho hình 9.73, biết rằng MN // AB, MP // AC. Hãy liệt kê ba cặp hai tam giác (khác nhau) đồng dạng có trong hình
Phương pháp:
Áp dụng định nghĩa hai tam giác đồng dạng
Lời giải:
+) ΔCNM ∽ ΔCAB (vì MN // AB) (1).
+) ΔMPB ∽ ΔCAB (vì MP // AC) (2).
Bài 9.42 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức
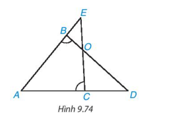
Cho hình 9.74, biết rằng \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\). Chứng minh rằng ΔABD ∽ ΔACE và ΔBOE ∽ ΔCOD
Phương pháp:
Chứng minh ΔBOE và ΔCOD có: \(\widehat {C{\rm{D}}O} = \widehat {BEO}\) và \(\widehat {EBO} = \widehat {DCO}\)
Lời giải:
- Xét tam giác ABD và tam giác ACE có 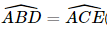 (giả thiết), góc A chung.
(giả thiết), góc A chung.
Suy ra ΔABD ∽ ΔACE (g.g).
- Vì ΔABD ∽ ΔACE nên 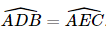 .
.
Suy ra 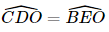 (1).
(1).
Lại có 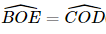 (hai góc đối đỉnh) (2).
(hai góc đối đỉnh) (2).
Từ (1) và (2) suy ra ΔBOE ∽ ΔCOD (g.g).
Bài 9.43 trang 110 SGK Toán 8 tập 2 - Kết nối tri thức
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng
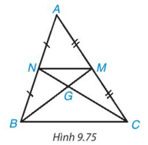
Phương pháp:
Chứng minh tam giác GMN và tam giác GBC có NM // BC
Lời giải:
Vì BM, CN là các đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC, AB.
Suy ra MN là đường trung bình của tam giác ABC.
Suy ra 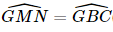 (hai góc ở vị trí so le trong).
(hai góc ở vị trí so le trong).
Mặt khác 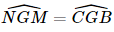 (hai góc đối đỉnh).
(hai góc đối đỉnh).
Do đó, ∆GMN ∽ ∆GBC (g.g).
Vì MN là đường trung bình của tam giác ABC nên BC = 2MN.
Khi đó, 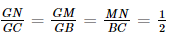 .
.
Vậy ∆GMN ∽ ∆GBC với tỉ số đồng dạng bằng 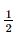
Bài 9.44 trang 111 SGK Toán 8 tập 2 - Kết nối tri thức
Cho tam giác ABC vuông tại A có AB=5cm, AC=4cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB
a) Chứng minh rằng ΔHDA ∽ ΔAHC
b) Tính độ dài các đoạn thẳng HA, HB, HC, HD
Phương pháp:
a) Chứng minh tam giác vuông HDA (vuông tại D) và tam giác vuông AHC (vuông tại H) có: \(\widehat {DHA} = \widehat {HAC}\)
b) Áp dụng định lý Pythagore trong tam giác vuông để tính HA, HB, HC, HD
Lời giải:
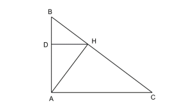
a) Ta có 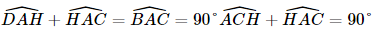 (do tam giác ACH vuông ở H).
(do tam giác ACH vuông ở H).
Suy ra 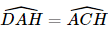 (cùng phụ với
(cùng phụ với 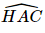 ).
).
Tam giác HDA vuông tại D và tam giác AHC vuông tại H có 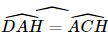 nên ΔHDA ∽ ΔAHC .
nên ΔHDA ∽ ΔAHC .
b) Áp dụng định lí Pythagore cho tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 42 + 52 = 41.
Suy ra BC=41">BC=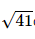 cm.
cm.
Diện tích tam giác ABC là: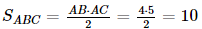 (cm2).
(cm2).
Lại có 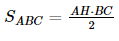 , do đó AH ∙ BC = 2 . 10 = 20, suy ra AH =
, do đó AH ∙ BC = 2 . 10 = 20, suy ra AH = (cm).
(cm).
Áp dụng định lí Pythagore cho tam giác ACH ta có AC2 = AH2 + CH2.
Do đó,CH2 = AC2 – AH2 = 42 –
Suy ra CH=1641">CH=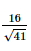 (cm).
(cm).
Vì ΔHDA ∽ ΔAHC nên 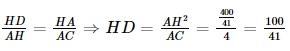 (cm).
(cm).
Ta có BH = BC – HC = 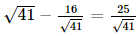 (cm).
(cm).
Bài 9.45 trang 111 SGK Toán 8 tập 2 - Kết nối tri thức
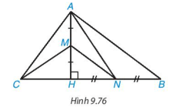
Cho tam giác ABC có đường cao AH. Biết AH=12cm, CH=9cm, BH=16cm. Lấy M, N lần lượt là trung điểm của AH, BH
a) Chứng minh rằng ABC là tam giác vuông tại A
b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN
c) Tính diện tích tam giác AMN
Phương pháp:
Áp dụng định lý Pythagore
Lời giải:
a) Xét tam giác AHB vuông tại H, có:
AH2 + HB2 = AB2 (định lý Pythagore)
Suy ra AB2 = 122 + 162 = 400.
Suy ra AB = 20 cm.
Tương tự, có: AC2 = AH2 + CH2 (áp dụng định lý Pythagore trong tam giác vuông AHC).
Suy ra AC2 = 122 + 92 = 225.
Suy ra AC = 15 cm.
Có BC = CH + BH = 9 + 16 = 25 cm.
Trong tam giác ABC, nhận thấy AB2 + AC2 = BC2 (do 202 + 152 = 252 = 625).
Suy ra tam giác ABC vuông tại A (định lí Pythagore đảo).
b) Xét tam giác AHB có:
M là trung điểm của AH
N là trung điểm của BH
Suy ra MN là đường trung bình của tam giác AHB.
Do đó, MN // AB. Mà AB ⊥ AC (vì tam giác ABC vuông tại A).
Suy ra MN ⊥ AC.
Xét ΔACN có AH ⊥ CN (gt), MN ⊥ AC (cmt), AH ∩ MN = {M}.
Vậy M là trực tâm của ΔACN, do đó CM ⊥ AN
c) Ta có: 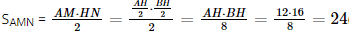 (cm2)
(cm2)
Bài 9.46 trang 111 SGK Toán 8 tập 2 - Kết nối tri thức
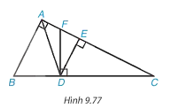
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{{B{\rm{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}\), từ đó suy ra \(A{\rm{E}} = \frac{{AB.AC}}{{AB + AC}}\)
b) ΔDFC ∽ ΔABC
c) DF=DB
Phương pháp:
Sử dụng các tam giác đồng dạng để chứng minh
Lời giải:
a) Vì AD là tia phân giác của góc BAC nên 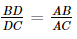 .
.
Suy ra BD . AC = DC . AB. (*)
Xét BD . (AB + AC) = BD . AB + BD . AC
= BD . AB + DC . AB (do (*))
= AB . (BD + DC)
= AB . BC.
Vậy BD . (AB + AC) = AB . BC. Suy ra 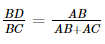 . (1)
. (1)
Hai tam giác CED vuông tại E và tam giác CAB vuông tại A có góc nhọn C chung nên
∆CED ∽ ∆CAB.
Suy ra 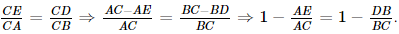
Do đó, 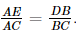 (2)
(2)
Từ (1) và (2) suy ra 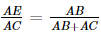 , do đó AE=AB⋅ACAB+AC">AE=
, do đó AE=AB⋅ACAB+AC">AE= .
.
b) Hai tam giác DFC vuông tại D và tam giác ABC vuông tại A có góc nhọn C chung nên
∆DFC ∽ ∆ABC.
c) Vì ∆DFC ∽ ∆ABC nên 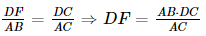 . (3)
. (3)
Từ (*) ta có DB=DC⋅ABAC">DB=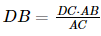 . (4)
. (4)
Từ (3) và (4) suy ra DB = DF.
Bài 9.47 trang 111 SGK Toán 8 tập 2 - Kết nối tri thức
Để tính được chiều cao gần đúng của kim tự tháp Ai Cập, người ta nắm 1 cây cọc cao 1m vuông góc với mặt đất và đo được bóng cây cọc trên mặt đất là 1,5m. Khi đó chiều dài bóng của kim tự tháp trên mặt đất là 208,2 m. Hỏi kim tự tháp cao bao nhiêu mét?
Phương pháp:
Chứng minh ΔB'A'C' ∽ ΔBAC từ đó suy ra tỉ số và tính AB
Lời giải:
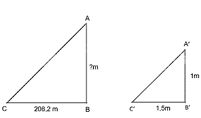
Giả sử AB là chiều cao của kim tự tháp với BC là bóng; A'B' là chiều cao cây cọc với bóng của nó trên mặt đất là B'C'.
Vì trong cùng một thời điểm, các tia nắng mặt trời tạo với mặt đất các góc bằng nhau.
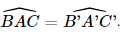 .
.Xét hai tam giác BAC (vuông tại B) và tam giác B'A'C' (vuông tại B') có 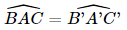 . Suy ra ΔB'A'C' ∽ ΔBAC.
. Suy ra ΔB'A'C' ∽ ΔBAC.
Do đó, 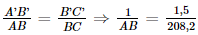
Suy ra AB = 208,2 : 1,5 = 138,8 (m).
Vậy kim tự tháp cao 138,8 m.
Bài 9.48 trang 111 SGK Toán 8 tập 2 - Kết nối tri thức
Từ căn hộ chung cư nhà mình, bạn Lan đứng cách cửa sổ 1m nhìn sang tòa nhà đối diện thì vừa nhìn thấy đúng tất cả 6 tầng của tòa nhà đó. Biết rằng cửa sổ nhà Lan cao 80cm và mỗi tầng của tòa nhà đối diện 4m. Hỏi khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là bao nhiêu?
Phương pháp:
Chứng minh ΔOAB ∽ ΔOCD suy ra các tỉ số đồng dạng và khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là 29m
Lời giải:
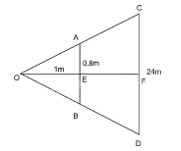
Giả sử O là vị trí bạn Lan đứng, AB là độ cao cửa sổ của nhà Lan, CD là độ cao của 6 tầng nhà đối diện mà Lan nhìn thấy. OE là khoảng cách từ vị trí bạn Lan đứng đến cửa sổ. OE cắt CD tại F.
Các điểm kí hiệu như trên hình vẽ.
Có OE = 1 m; AB = 80 cm = 0,8 m; CD = 6 ∙ 4 = 24 m.
Xét tam giác OAB và tam giác OCD có AB // CD (do các tòa nhà thẳng đứng vuông góc với mặt đất). Suy ra ΔOAB ∽ ΔOCD.
Do đó, 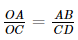 .
.
Xét tam giác OAE và tam giác OCF có AE // CF (do AB // CD). Suy ra ΔOAE ∽ ΔOCF.
Do đó, 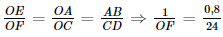 .
.
Suy ra OF = 24 : 0,8 = 30 (m).
Do đó, EF = OF – OE = 30 – 1 = 29 (m).
Vậy khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là 29 m.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,15 trang 135,136 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.15, 10.16, 10.17, 10.18, 10.19, 10.20, 10.21, 10.22, 10.23, 10.24 trang 123, 124 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.11, 10.12, 10.13, 10.14 trang 121, 122 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.5, 10.6, 10.7, 10.8, 10.9, 10.10 trang 120 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.1, 10.2, 10.3, 10.4 trang 116 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Bài tập ôn tập cuối năm
- Bài tập cuối chương 10
- Luyện tập chung (trang 121)
- Bài 39. Hình chóp tứ giác đều
- Bài 38. Hình chóp tam giác đều
- CHƯƠNG X. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
- Bài tập cuối chương 9
- Luyện tập chung (trang 108)
- Bài 37.Hình đồng dạng
- Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!