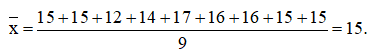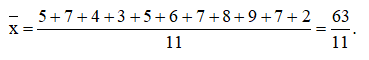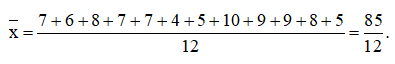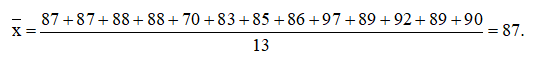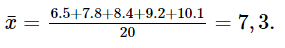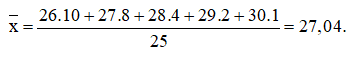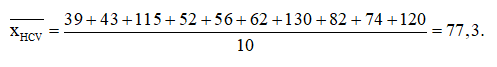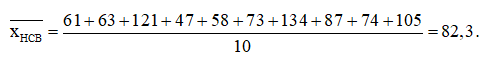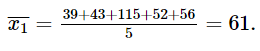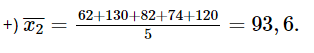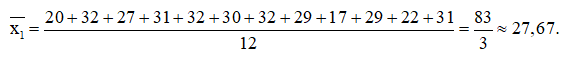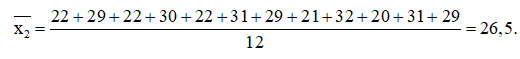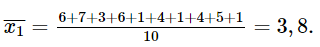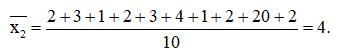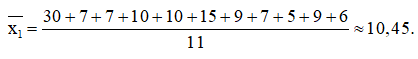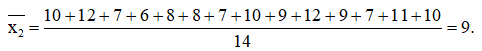Giải SBT Toán 10 trang 122, 123, 124 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4 trang 122, bài 5, 6, 7 trang 123, bài 8 trang 124 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 1. Tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:
Bài 1 trang 122 SBT Toán 10 - Chân trời sáng tạo
Tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:
a) \(15;15;12;14;17;16;16;15;15.\)
b) \(5;7;4;3;5;6;7;8;9;7;2.\)
c) \(7;6;8;7;7;4;5;10;9;9;8;5.\)
d) \(87;87;88;88;70;83;85;86;97;89;92;89;90.\)
Phương pháp:
- số trung bình: \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
- Chỉ ra mốt là giá trị có tần số lớn nhất.
Lời giải:
a) Ta có: n = 9
Sắp xếp mẫu số liệu theo thứ tự không giảm:
12; 14; 15; 15; 15; 15; 16; 16; 17
+) Số trung bình:
+) Vì n = 9 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 15.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 12; 14; 15; 15.
Vậy Q1 = (14 + 15) : 2 = 14,5.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, không kể Q2 vì n là số lẻ: 15; 16; 16; 17.
Vậy Q3 = (16 + 16) : 2 = 16.
+) Vì số 15 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (4 lần). Nên suy ra Mốt của mẫu số liệu là Mo = 15.
b) Ta có: n = 11
Sắp xếp mẫu số liệu theo thứ tự không giảm:
2; 3; 4; 5; 5; 6; 7; 7; 7; 8; 9
+) Số trung bình:
+) Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 6.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 2; 3; 4; 5; 5.
Vậy Q1 = 4.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, không kể Q2 vì n là số lẻ: 7; 7; 7; 8; 9.
Vậy Q3 = 7.
+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là Mo = 7.
c) Ta có: n = 12
Sắp xếp mẫu số liệu theo thứ tự không giảm:
4; 5; 5; 6; 7; 7; 7; 8; 8; 9; 9; 10
+) Số trung bình:
+) Vì n = 12 là số chẵn nên ta có tứ phân vị thứ hai Q2 = (7 + 7) : 2 = 7.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 4; 5; 5; 6; 7; 7.
Vậy Q1 = (5 + 6) : 2 = 5,5.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 7; 8; 8; 9; 9; 10.
Vậy Q3 = (8 + 9) : 2 = 8,5.
+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là Mo = 7.
d) Ta có: n = 13
Sắp xếp mẫu số liệu theo thứ tự không giảm:
70; 83; 85; 86; 87; 87; 88; 88; 89; 89; 90; 92; 97
+) Số trung bình:
+) Vì n = 13 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 88.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 70; 83; 85; 86; 87; 87.
Vậy Q1 = (85 + 86) : 2 = 85,5.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, không kể Q2 vì n là số lẻ: 88; 89; 89; 90; 92; 97.
Vậy Q3 = (89 + 90) : 2 = 89,5.
+) Vì số 87, 88, 89 là các giá trị xuất hiện nhiều nhất trong mẫu số liệu (2 lần). Nên suy ra Mốt của mẫu số liệu là Mo ∈ {87; 88; 89}.
Bài 2 trang 122 SBT Toán 10 - Chân trời sáng tạo
Hãy tìm số trung bình, tứ phân vị và mốt của các số liệu sau:
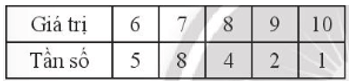
a)
|
Giá trị |
6 |
7 |
8 |
9 |
10 |
|
Tần số |
5 |
8 |
4 |
2 |
1 |
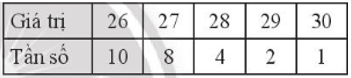
b)
|
Giá trị |
26 |
27 |
28 |
29 |
30 |
|
Tần số |
10 |
8 |
4 |
2 |
1 |
Phương pháp:
- Dùng công thức tìm số trung bình \(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}}}{n}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
- Chỉ ra mốt là giá trị có tần số lớn nhất.
Lời giải:
a)
Ta có: n = 5 + 8 + 4 + 2 + 1 = 20
Sắp xếp mẫu số liệu theo thứ tự không giảm:
6; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 9; 10
+) Số trung bình:
+) Vì n = 20 là số chẵn nên ta có tứ phân vị thứ hai Q2 = (7 + 7) : 2 = 7.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 6; 6; 6; 6; 6; 7; 7; 7; 7; 7.
Vậy Q1 = (6 + 7) : 2 = 6,5.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 7; 7; 7; 8; 8; 8; 8; 9; 9; 10.
Vậy Q3 = (8 + 8) : 2 = 8.
+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (8 lần). Nên suy ra Mốt của mẫu số liệu là Mo = 7.
b)
Ta có: n = 10 + 8 + 4 + 2 + 1 = 25
Sắp xếp mẫu số liệu theo thứ tự không giảm:
26; 26; 26; 26; 26; 26; 26; 26; 26; 26; 27; 27; 27; 27; 27; 27; 27; 27; 28; 28; 28; 28; 29; 29; 30
+) Số trung bình:
+) Vì n = 25 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 27.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 26; 26; 26; 26; 26; 26; 26; 26; 26; 26; 27; 27.
Vậy Q1 = (26 + 26) : 2 = 26.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, không kể Q2 vì n là số lẻ: 27; 27; 27; 27; 27; 28; 28; 28; 28; 29; 29; 30.
Vậy Q3 = (28 + 28) : 2 = 28.
+) Vì số 26 là các giá trị xuất hiện nhiều nhất trong mẫu số liệu (10 lần). Nên suy ra Mốt của mẫu số liệu là Mo = 26.
Bài 3 trang 122 SBT Toán 10 - Chân trời sáng tạo
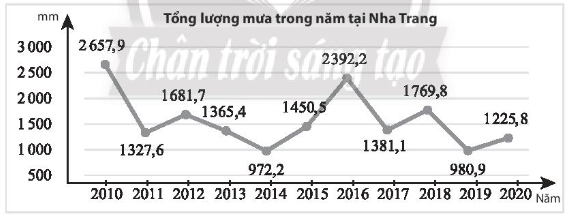
Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau (đơn vị: mm).
a) Hãy tính lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020.
b) Hãy tìm các tứ phân vị của mẫu số liệu đó.
Phương pháp:
- Dùng công thức tính số trung bình: \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
- Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Lời giải:
a) Từ năm 2010 đến 2020 có tất cả 11 năm
Lượng mưa trung bình tại trạm quan trắc trên từ năm 2010 đến 2020 là:
b) Sắp xếp lượng mưa các năm theo thứ tự không giảm là:
972,2; 980,9; 1225,8; 1327,6; 1365,4; 1381,1; 1450,5; 1681,7; 1769,8; 2392,2; 2657,9
Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 1381,1.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 972,2; 980,9; 1225,8; 1327,6; 1365,4.
Vậy Q1 = 1225,8.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, không kể Q2 vì n là số lẻ: 1450,5; 1681,7; 1769,8; 2392,2; 2657,9.
Vậy Q3 = 1769,8.
Bài 4 trang 122 SBT Toán 10 - Chân trời sáng tạo
Số huy chương vàng và bạc trong các giải thể thao quốc tế mà đoàn thể thao Việt Nam đạt được tại các giải đấu ở Châu Á trong các năm từ năm 2010 đến 2019 được thống kê ở bảng sau:
|
Năm |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
|
Huy chương vàng |
39 |
43 |
115 |
52 |
56 |
62 |
130 |
82 |
74 |
120 |
|
Huy chương bạc |
61 |
63 |
121 |
47 |
58 |
73 |
134 |
87 |
74 |
105 |
( Nguồn: Tổng cục thống kê)
a) Tìm số trung bình và trung vị huy chương vàng và huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên.
b) Hãy so sánh số huy chương vàng đoàn thể thao Việt Nam đạt được trong gia đoạn 2010- 2014 với giai đoạn 2015-1019.
Phương pháp:
Tìm số trung bình theo công thức \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
Sắp xếp và chỉ ra trung vị
Lời giải:
a) Từ năm 2010 đến 2019 có tất cả 10 năm.
+) Trung bình số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong 10 năm trên là:
+) Trung bình số huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên là:
+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong 10 năm trên theo thứ tự không giảm là:
39; 43; 52; 56; 62; 74; 82; 115; 120; 130.
Vì n = 10 là số chẵn nên trung vị số huy chương vàng đạt được trong 10 năm là: (62 + 74) : 2 = 68.
+) Sắp xếp mẫu số liệu số huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên theo thứ tự không giảm là:
47; 58; 61; 63; 73; 74; 87; 105; 121; 134.
Vì n = 10 là số chẵn nên trung vị số huy chương bạc đạt được trong 10 năm là: (73 + 74) : 2 = 73,5.
b) * Từ năm 2010 – 2014 có 5 năm
+) Trung bình số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 là:
+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 theo thứ tự không giảm là:
39; 43; 52; 56; 115.
Vì n1 = 5 là số lẻ nên trung vị số huy chương vàng đạt được trong giai đoạn 2010 – 2014 là: 52.
* Từ năm 2015 – 2019 có 5 năm
+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2015 – 2019 theo thứ tự không giảm là:
62; 74; 82; 120; 130.
Vì n2 = 5 là số lẻ nên trung vị số huy chương vàng đạt được trong giai đoạn 2015 – 2019 là: 82.
Vậy nếu so sánh theo số trung bình và số trung vị thì Việt Nam đều giành được nhiều huy chương vàng hơn trong giai đoạn 2015 – 2019 so với giai đoạn 2010 – 2014.
Bài 5 trang 123 SBT Toán 10 - Chân trời sáng tạo
Bảng sau ghi lại độ tuổi của 2 nhóm vận động viên tham gia một cuộc thi
|
Nhóm 1 |
20 |
32 |
27 |
31 |
32 |
30 |
32 |
29 |
17 |
29 |
22 |
31 |
|
Nhóm 2 |
22 |
29 |
22 |
30 |
22 |
31 |
29 |
21 |
32 |
20 |
31 |
29 |
a) Hãy so sánh độ tuổi hai nhóm vận động viên theo số trung bình và trung vị.
b) Tìm tứ phân vị của độ tuổi vận động viên hai nhóm gộp lại.
Phương pháp:
Tính số trung bình và trung vị của độ tuổi hai nhóm động viên sau đó so sánh.
Sắp xếp và tìm tứ phân vị
Lời giải:
a)
+) Nhóm 1 có tất cả 12 vận động viên
Sắp xếp mẫu số liệu theo thứ tự không giảm:
17; 20; 22; 27; 29; 29; 30; 31; 31; 32; 32; 32
Số trung bình:
Vì n = 12 là số chẵn nên số trung vị của mẫu số liệu ở nhóm 1 là:
Me1 = (29 + 30) : 2 = 29,5.
+) Nhóm 2 có tất cả 12 vận động viên
Sắp xếp mẫu số liệu theo thứ tự không giảm:
20; 21; 22; 22; 29; 29; 29; 29; 30; 31; 31; 32
Số trung bình:
Vì n = 12 là số chẵn nên số trung vị của mẫu số liệu ở nhóm 2 là:
Me2 = (29 + 29) : 2 = 29
Vậy nếu so sánh theo số trung bình và số trung vị thì độ tuổi của các vận động viên nhóm 1 cao hơn nhóm 2.
b) Cả hai nhóm gộp lại có tất cả 24 vận động viên
Sắp xếp độ tuổi của các vận động viên theo thứ tự không giảm ta có mẫu số liệu:
17; 20; 20; 21; 22; 22; 22; 27; 29; 29; 29; 29; 29; 29; 30; 30; 31; 31; 31; 31; 32; 32; 32; 32
Vì n = 24 là số chẵn nên ta có tứ phân vị thứ hai Q2 = (29 + 29) : 2 = 29.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 17; 20; 20; 21; 22; 22; 22; 27; 29; 29; 29; 29.
Vậy Q1 = (22 + 22) : 2 = 22.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 29; 29; 30; 30; 31; 31; 31; 31; 32; 32; 32; 32.
Vậy Q3 = (31 + 31) : 2 = 31.
Bài 6 trang 123 SBT Toán 10 - Chân trời sáng tạo
Minh và Thủy ghi lại số thư điện tử mà mỗi người nhận được mỗi ngày trong 10 ngày được lựa chọn ngẫu nhiên từ tháng 01/2021 ở bảng sau:
|
Minh |
6 |
7 |
3 |
6 |
1 |
4 |
1 |
4 |
5 |
1 |
|
Thủy |
2 |
3 |
1 |
2 |
3 |
4 |
1 |
2 |
20 |
2 |
a) Hãy tìm số trung bình, trung vị và mốt của số thư điện tử mà mỗi bạn nhận được theo số liệu trên.
b) Nếu so sánh theo số trung bình thì ai nhận được nhiều thư điện tử hơn?
c) Nếu so sánh theo số trung vị thì ai nhận được nhiều thư điện tử hơn?
d) Nên dùng số trung bình hay số trung vị để so sanh xem ai nhận được nhiều thư điện tử hơn mỗi ngày?
Phương pháp:
Tìm số trung bình theo công thức \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
Tìm số trung vị và mốt
Lời giải:
a)
+) Sắp xếp số thư điện tử mà Minh nhận được trong 10 ngày theo thứ tự không giảm: 1; 1; 1; 3; 4; 4; 5; 6; 6; 7
Số trung bình của số thư điện tử mà bạn Minh nhận được:
Vì n = 10 là số lẻ nên trung vị số thư điện tử mà Minh nhận được trong 10 ngày là: Me1 = (4 + 4) : 2 = 4.
Vì giá trị 1 xuất hiện nhiều nhất (3 lần) nên suy ra mốt của mẫu số liệu trên là Mo1 = 1.
+) Sắp xếp số thư điện tử mà Thủy nhận được trong 10 ngày theo thứ tự không giảm: 1; 1; 2; 2; 2; 2; 3; 3; 4; 20
Số trung bình của số thư điện tử mà bạn Thủy nhận được:
Vì n = 10 là số lẻ nên trung vị số thư điện tử mà Thủy nhận được trong 10 ngày là: Me2 = (2 + 2) : 2 = 2.
Vì giá trị 2 xuất hiện nhiều nhất (4 lần) nên suy ra mốt của mẫu số liệu trên là Mo2 = 2.
b) Nếu so sánh theo số trung bình thì Thủy nhận được nhiều thư điện tử hơn Minh (4 > 3,8).
c) Nếu so sánh theo số trung vị thì Minh nhận được nhiều thư điện tử hơn Thủy (4 > 2)
d) Nên dùng số trung vị để so sánh xem ai nhận được nhiều thư điện tử hơn mỗi ngày vì trong bảng thống kê ta thấy dãy số liệu của bạn Thủy có một số liệu quá lớn so với các số liệu còn lại (là số 20).
Bài 7 trang 123 SBT Toán 10 - Chân trời sáng tạo
Bạn Út ghi lại khối lượng của một số quả xoài Keo và xoài Thanh Ca ở bảng sau ( đơn vị: gam)
|
Xoài Keo |
370 |
320 |
350 |
290 |
300 |
350 |
310 |
330 |
340 |
370 |
390 |
|
|
Xoài Thanh Ca |
350 |
310 |
410 |
390 |
380 |
370 |
320 |
350 |
330 |
340 |
370 |
400 |
a) Sử dụng số trung bình, hãy so sánh khối lượng của hai loại xoài
b) Sử dụng trung vị, hãy so sánh khối lượng của hai loại xoài.
c) Hãy tính tứ phân vị của hai mẫu số liệu trên.
d) Nếu bạn Út mua 5kg xoài Keo thì sẽ được khoảng bao nhiêu quả?
Nếu bạn Út mua 5kg xoài Thanh Ca thì sẽ được khoảng bao nhiêu quả?
Phương pháp:
Tìm số trung bình theo công thức \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
Tìm số trung vị và tứ phân vị
Lời giải:
a) +) Xoài Keo có tất cả 11 quả được chọn để ghi khối lượng.
Khối lượng trung bình của khối lượng Xoài Keo là:
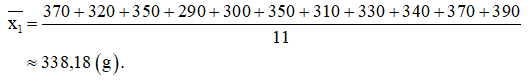
+) Xoài Thanh Ca có tất cả 12 quả được chọn để ghi khối lượng.
Khối lượng trung bình của khối lượng Xoài Thanh Ca là:
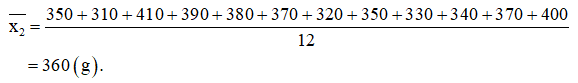
Vậy nếu so sánh theo số trung bình thì khối lượng xoài Thanh Ca cao hơn khối lượng xoài Keo.
b) +) Sắp xếp khối lượng mỗi quả Xoài Keo theo thứ tự không giảm:
290; 300; 310; 320; 330; 340; 350; 350; 370; 370; 390
Vì n = 11 là số lẻ nên số trung vị của khối lượng xoài Keo là:
Me1 = 340 (g).
+) Sắp xếp khối lượng mỗi quả Xoài Thanh Ca theo thứ tự không giảm:
310; 320; 330; 340; 350; 350; 370; 370; 380; 390; 400; 410
Vì n = 12 là số chẵn số trung vị của khối lượng xoài Thanh Ca là:
Me2 = (350 + 370) : 2 = 360 (g).
Vậy nếu so sánh theo số trung vị thì khối lượng xoài Thanh Ca cao hơn khối lượng xoài Keo.
c) +) Sắp xếp khối lượng mỗi quả Xoài Keo theo thứ tự không giảm:
290; 300; 310; 320; 330; 340; 350; 350; 370; 370; 390
Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 340.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 290; 300; 310; 320; 330.
Vậy Q1 = 310.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, không kể Q2 vì n là số lẻ: 350; 350; 370; 370; 390.
Vậy Q3 = 370.
+) Sắp xếp khối lượng mỗi quả Xoài Thanh Ca theo thứ tự không giảm:
310; 320; 330; 340; 350; 350; 370; 370; 380; 390; 400; 410
Vì n = 12 là số chẵn nên ta có tứ phân vị thứ hai
Q2 = (350 + 370) : 2 = 360.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 310; 320; 330; 340; 350; 350.
Vậy Q1 = (330 + 340) : 2 = 335.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 370; 370; 380; 390; 400; 410.
Vậy Q3 = (380 + 390) : 2 = 385.
d) Do 5 000 : 338,18 ≈ 14,79 nên nếu bạn Út mua 5 kg xoài Keo thì sẽ mua được khoảng 14 đến 15 quả.
Do 5 000 : 360 ≈ 13,89 nên nếu bạn Út mua 5 kg xoài Thanh Ca thì sẽ mua được khoảng 13 đến 14 quả.
Bài 8 trang 124 SBT Toán 10 - Chân trời sáng tạo
Số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố khu vực Đồng bằng sông Hồng và khu vực Trung du và miền núi phía Bắc vào năm 2019 được cho như sau:
Đồng bằng sông Hồng: 30; 7; 7; 10; 10; 15; 9; 7; 5; 9; 6.
Trung du và miền núi phía Bắc: 10; 12; 7; 6; 8; 8; 7; 10; 9; 12; 9; 7; 11; 10.
( Nguồn: Tổng cục thống kê)
a) Mỗi khu vực nêu trên có bao nhiêu tỉnh/thành phố?
b) Sử dụng số trung bình hãy so sánh số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố ở hai khu vực.
c) Sử dụng số trung vị hãy so sánh số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố ở hai khu vực.
d) Hãy giải thích tại sao lại có sự khác biệt khi so sánh bằng số trung bình và trung vị.
e) Hãy tìm tứ phân vị và mốt của hai khu vực.
Phương pháp:
Đếm số liệu mỗi khu vực
Tìm số trung bình theo công thức \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
Tìm số trung vị, tứ phân vị và mốt
Lời giải:
a) Khu vực Đồng bằng Sông Hồng có 11 tỉnh/thành phố (do có 11 số liệu trong dãy số liệu). Khu vực Trung du và miền núi phía Bắc có 14 tỉnh/thành phố (do có 14 số liệu trong dãy số liệu).
b)
+) Trung bình số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng vào năm 2019 là:
+)Trung bình số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Trung du và miền núi phía Bắc vào năm 2019 là:
Vậy theo số trung bình thì các các tỉnh/ thành phố khu vực Đồng bằng sông Hồng có nhiều đơn vị hành chính cấp quận/ huyện/ thị xã hơn khu vực Trung du và miền núi phía Bắc.
c)
+) Sắp xếp số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng vào năm 2019 theo thứ tự không giảm:
5; 6; 7; 7; 7; 9; 9; 10; 10; 15; 30
Vì n = 11 là số lẻ nên số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng vào năm 2019 là:
Me1 = 9.
+) Sắp xếp số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Trung du và miền núi phía Bắc vào năm 2019 theo thứ tự không giảm:
6; 7; 7; 7; 8; 8; 9; 9; 10; 10; 10; 11; 12; 12
Vì n = 14 là số chẵn nên số trung vị của số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Trung du và miền núi phía Bắc vào năm 2019 là:
Me2 = (9 + 9) : 2 = 9.
Vậy nếu so sánh theo số trung vị thì số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng và Trung du và miền núi phía Bắc là bằng nhau.
d) Có sự khác biệt khi so sánh bằng số trung bình và số trung vị là do có một tỉnh/ thành phố khu vực ĐBSH có quá nhiều đơn vị hành chính cấp quận/ huyện/ thị xã so với các tỉnh/ thành phố khác.
e)
+) Đồng bằng Sông Hồng:
Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q2 = 9.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, không kể Q2 vì n là số lẻ: 5; 6; 7; 7; 7.
Vậy Q1 = 7.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, không kể Q2 vì n là số lẻ: 9; 10; 10; 15; 30.
Vậy Q3 = 10.
Vì giá trị 7 xuất hiện nhiều nhất (3 lần) nên suy ra mốt của mẫu số liệu trên là Mo = 7.
+) Trung du và miền núi phía Bắc:
Vì n = 14 là số chẵn nên ta có tứ phân vị thứ hai
Q2 = (9 + 9) : 2 = 9.
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 6; 7; 7; 7; 8; 8; 9.
Vậy Q1 = 7.
Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 9; 10; 10; 10; 11; 12; 12.
Vậy Q3 = 10.
Vì giá trị 7 và 10 xuất hiện nhiều nhất (3 lần) nên suy ra mốt của mẫu số liệu trên là Mo ∈ {7; 10}.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SBT Toán 10 trang 102, 103 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 100, 101 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 95, 96, 97 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 77, 78, 79, 80 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 75, 76 Chân trời sáng tạo tập 2 (30/01)
- Bài tập cuối chương X - SBT Toán 10 CTST
- Bài 2. Xác suất của biến cố - SBT Toán 10 CTST
- Bài 1. Không gian mẫu và biến cố - SBT Toán 10 CTST
- Chương X. Xác suất - SBT Toán 10 CTST
- Bài tập cuối chương IX - SBT Toán 10 CTST
- Bài 4. Ba đường conic trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 3. Đường tròn trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 2. Đường thẳng trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 1. Tọa độ của vectơ - SBT Toán 10 CTST
- Chương IX. Phương pháp tọa độ trong mặt phẳng - SBT Toán 10 CTST
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!