Giải SBT Toán 10 trang 34, 35, 36 Chân trời sáng tạo tập 1

A. TRẮC NGHIỆM

Bài 1 trang 34 SBT Toán 10 - Chân trời sáng tạo

Bạn Danh để dành được 900 nghìn đồng. Trong một đợt ủng hộ trẻ em mồ côi, Danh đã lấy ra x tờ 50 nghìn đồng, y tờ tiền 100 nghìn đồng để trao tặng. Một bất phương trình mô tả điều kiện ràng buộc với x, y là:

A. \(50x + 100y \le 900\)                    B. \(50x + 100y \ge 900\)

C. \(100x + 50y \le 900\)                    D. \(x + y = 900\)

Lời giải:

Đáp án đúng là: A

Ta có x tờ tiền loại 50 nghìn đồng thì có giá trị là 50x (nghìn đồng).

y tờ tiền loại 100 nghìn đồng thì có giá trị là 100y (nghìn đồng).

Tổng số tiền bạn Danh trao tặng là: 50x + 100y (nghìn đồng).

Mà bạn Danh có 900 nghìn đồng nên 50x + 100y ≤ 900.

Vậy bất phương trình mô tả điều kiện ràng buộc đối với x, y là 50x + 100y ≤ 900.

Bài 2 trang 34 SBT Toán 10 - Chân trời sáng tạo

Trong các bất phương trình sau, bất phương trình nào không phải là bất phương trình bậc nhất hai ẩn?

A. \(2x - 3y - 2022 \le 0\)     

B. \(5x + y \ge 2x + 11\)

C. \(x + 2025 > 0\)       

D. \(\frac{x}{y} + 1 > 0\)

Lời giải:

Đáp án đúng là: D

Xét đáp án A, 2x – 3y – 2022 ≤ 0 ⇔ 2x – 3y ≤ 2022, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by ≤ c (a, b, c là các số thực, a, b không đồng thời bằng 0).

Xét đáp án B, 5x + y ≥ 2x + 11 ⇔ 3x + y ≥ 11, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by ≥ c (a, b, c là các số thực, a, b không đồng thời bằng 0).

Xét đáp án C, x + 2025 > 0 ⇔ x + 0y > – 2025, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by > c (a, b, c là các số thực, a, b không đồng thời bằng 0).

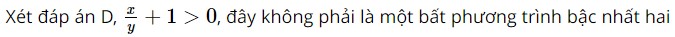
ẩn vì nó không có một trong các dạng ax + by < c, ax + by > c, ax + by ≤ c, ax + by ≥ c với a, b, c là các số thực, a, b không đồng thời bằng 0.

Bài 3 trang 34 SBT Toán 10 - Chân trời sáng tạo

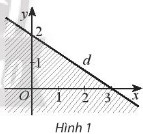
Miền không gạch chéo (không kể bờ d) trong hình 11 là miền nghiệm của bất phương trình nào trong các bất phương trình sau đây:

A. \(2x + 3y < 6\)

B. \(2x + 3y > 6\)

C. \(\frac{x}{2} + \frac{y}{3} > 0\)   

D. \(\frac{x}{2} + \frac{y}{3} < 1\)

Lời giải:

Đáp án đúng là: B

Đường thẳng d có dạng: y = ax + b.

Từ Hình 1, ta thấy đường thẳng d đi qua hai điểm có tọa độ (3; 0) và (0; 2).

Xét điểm O(0; 0) thuộc miền bị gạch chéo, ta có: 2 . 0 + 3 . 0 = 0 < 6.

Mà điểm O(0; 0) không thuộc miền nghiệm của bất phương trình ở Hình 1 nên bất phương trình cần tìm là 2x + 3y > 6 (không lấy dấu = vì miền nghiệm không kể bờ d).

Bài 4 trang 34 SBT Toán 10 - Chân trời sáng tạo

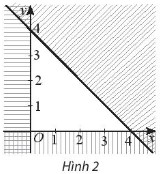
Miền tam giác không gạch chéo trong hình 2 là miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình nào dưới đấy?

A. \(\left\{ \begin{array}{l}x + y - 4 \ge 0\\x \le 0\\y \ge 0\end{array} \right.\)   

B. \(\left\{ \begin{array}{l}x + y - 4 \ge 0\\x \ge 0\\y \le 0\end{array} \right.\)

C. \(\left\{ \begin{array}{l}x + y \ge 4\\x \ge 0\\y \ge 0\end{array} \right.\)   

D. \(\left\{ \begin{array}{l}x + y - 4 \ge 0\\x \le 0\\y \le 0\end{array} \right.\)

Lời giải:

Dễ thấy gốc tọa độ (0; 0) không thuộc miền nghiệm => Loại A, D.

Điểm (1;0) không thuộc miền nghiệm => Loại C

Chọn B.

Bài 5 trang 35 SBT Toán 10 - Chân trời sáng tạo

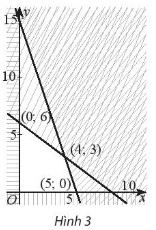
Biểu thức \(F = 2x - 8y\) đạt GTNN bằng bao nhiêu trên miền đa giác không gạch chéo trong hình 3?

A. \( - 48\) 

B. 0

C. \( - 160\) 

D.\( - 40\)

Lời giải:

Đáp án đúng là: A

Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).

Người ta chứng minh được rằng biểu thức F = 2x – 8y đạt GTNN tại các đỉnh của đa giác.

Ta có: F(0; 0) = 2 . 0 – 8 . 0 = 0

F(0; 6) = 2 . 0 – 8 . 6 = – 48

F(4; 3) = 2 . 4 – 8 . 3 = – 16

F(5; 0) = 2 . 5 – 8 . 0 = 10

Vì – 48 < – 16 < 0 < 10.

Do đó, F đạt GTNN bằng – 48 tại đỉnh có tọa độ (0; 6).

Bài 6 trang 35 SBT Toán 10 - Chân trời sáng tạo

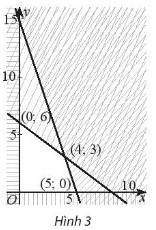
Biểu thức \(F = 5x + 2y\) đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong hình 3?

A. 30

B. 12   

C. 25   

D. 26

Phương pháp:

Biểu thức đạt GTLN hay GTNN tại các đỉnh của miền đa giác nghiệm.

Lời giải:

Đáp án đúng là: D

Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).

Người ta chứng minh được rằng biểu thức F = 5x + 2y đạt GTLN tại các đỉnh của đa giác.

Ta có: F(0; 0) = 5 . 0 + 2 . 0 = 0

F(0; 6) = 5. 0 + 2 . 6 = 12

F(4; 3) = 5 . 4 + 2 . 3 = 26

F(5; 0) = 5 . 5 + 2. 0 = 25

Vì 0 < 12 < 25 < 26.

Vậy F đạt GTLN bằng 26 tại đỉnh có tọa độ (4; 3).

B. TỰ LUẬN

Bài 1 trang 35 SBT Toán 10 - Chân trời sáng tạo

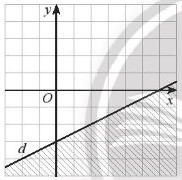
Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong hình 4 (mỗi ô vuông có cạnh là 1 đơn vị)

Phương pháp:

Bước 1: Gọi phương trình tổng quát của đường thẳng bờ

Bước 2: Xác định các điểm đường thẳng đi qua và xác định phương trình

Bước 3: Thay tọa độ điểm O(0;0) là nghiệm của bất phương trình cần tìm và xác định dấu của bất phương trình

Lời giải:

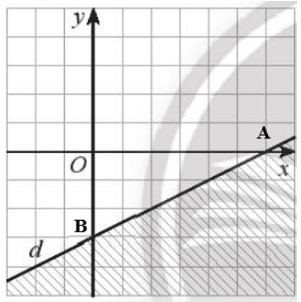
Gọi dạng đường thẳng d: y = ax + b.

Ta có đường thẳng d đi qua hai điểm A và B. Điểm A nằm trên tia Ox và cách O một khoảng bằng 6 cạnh ô vuông, do đó tọa độ A là A(6; 0). Điểm B nằm trên Oy và nằm phía dưới điểm O, cách O một khoảng 3 cạnh ô vuông nên B(0; – 3).

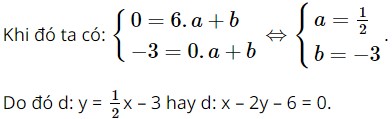
Xét điểm O(0; 0) thuộc miền nghiệm của bất phương trình cần tìm.

Ta có: 0 – 2 . 0 – 6 = – 6 < 0.

Do đó, bất phương trình cần tìm có dạng x – 2y – 6 ≤ 0 (do miền nghiệm bao gồm cả bờ d).

Bài 2 trang 35 SBT Toán 10 - Chân trời sáng tạo

Đường thẳng \(4x + 3y = 12\) và hai trục tọa độ chia mặt phẳng Oxy thành các miền như hình 5. Hãy tìm hệ bất phương trình có miền nghiệm là miền B (kể cả bờ)

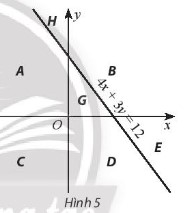
Lời giải:

Quan sát Hình 5, ta thấy miền B (kể cả bờ) nằm bên trên trục Ox (là miền nghiệm của bất phương trình y ≥ 0), bên phải trục Oy (là miền nghiệm của bất phương trình x ≥ 0) và không chứa điểm O(0; 0), lại có 4 . 0 + 3 . 0 = 0 < 12, do đó miền B nằm trong miền nghiệm của bất phương trình 4x + 3y ≥ 12.

Bài 3 trang 35 SBT Toán 10 - Chân trời sáng tạo

Tìm giá trị của F và G tương ứng với các giá trị x, y được cho trong bảng dưới đây:

Trong các giá trị tìm được:

a) Tìm GTLN của F

b) Tìm GTNN của G

Lời giải:

+ Với x = 0, y = 2, ta có: F = 4 . 0 + 5 . 2 = 10, G = 5 . 0 – 3 . 2 = – 6.

+ Với x = 0, y = 4, ta có: F = 4 . 0 + 5 . 4 = 20, G = 5 . 0 – 3 . 4 = – 12.

+ Với x = 1, y = 0, ta có: F = 4 . 1 + 5 . 0 = 4, G = 5 . 1 – 3 . 0 = 5.

+ Với x = 1, y = 1, ta có: F = 4 . 1 + 5 . 1 = 9, G = 5 . 1 – 3 . 1 = 2.

+ Với x = 2, y = 0, ta có: F = 4 . 2 + 5 . 0 = 8, G = 5 . 2 – 3 . 0 = 10.

+ Với x = 2, y = 1, ta có: F = 4 . 2 + 5 . 1 = 13, G = 5 . 2 – 3 . 1 = 7.

+ Với x = 4, y = 0, ta có: F = 4 . 4 + 5 . 0 = 16, G = 5 . 4 – 3 . 0 = 20.

Vậy ta hoàn thành được bảng như sau:

Từ bảng trên ta có:

a) GTLN của F là 20.

b) GTNN của G là – 12.

Bài 4 trang 36 SBT Toán 10 - Chân trời sáng tạo

Trên miền đa giác không gạch chéo ở hình 6, hãy:

a) Tìm GTLN của \(F = 2x + 3y\)

b) Tìm GTNN của \(G = x - 4y\)

Lời giải:

Miền đa giác không gạch chéo ở Hình 6 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3) và (5; 0).

a) Người ta chứng minh được rằng biểu thức F = 2x + 3y đạt GTLN tại các đỉnh của đa giác không bị gạch trên Hình 6.

Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0

F(0; 6) = 2 . 0 + 3 . 6 = 18

F(4; 3) = 2 . 4 + 3 . 3 = 14

F(5; 0) = 2 . 5 + 3 . 0 = 10.

Vì 0 < 10 < 14 < 18 nên GTLN của F là 18 tại đỉnh có tọa độ (0; 6).

b) Người ta chứng minh được rằng biểu thức G = x – 4y đạt GTNN tại các đỉnh của đa giác không bị gạch trên Hình 6.

Ta có: G(0; 0) = 0 – 4 . 0 = 0

G(0; 6) = 0 – 4 . 6 = – 24

G(4; 3) = 4 – 4 . 3 = – 8

G(5; 0) = 5 – 4 . 0 = 5

Vì – 24 < – 8 < 0 < 5 nên GTNN của G là – 24 tại đỉnh có tọa độ (0; 6).

Bài 5 trang 36 SBT Toán 10 - Chân trời sáng tạo

Bác Dũng dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Bác chỉ có không quá 9 triệu đồng để mua hạt giống. Cho biết tiền mua hạt giống cà tím 200 000 đồng/sào và cà chua là 100 000 đồng/sào. Viết hệ phương trình mô tả điều kiện ràng buộc đối với x, y

Lời giải:

Do x và y lần lượt là số sào đất bác Dũng dự định quy hoạch để trồng cà tím và cà chua nên x ≥ 0, y ≥ 0.

Để trồng x sào đất cà tím, cần số tiền mua hạt giống là 200 000x đồng.

Để trồng y sào đất cà chua, cần số tiền mua hạt giống là 100 000y đồng.

Vì bác Dũng chỉ có không quá 9 triệu đồng để mua hạt giống nên 200 000x + 100 000y ≤ 9 000 000 ⇔ 2x + y ≤ 90.

Vậy ta có hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y là

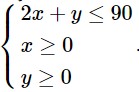
Bài 6 trang 36 SBT Toán 10 - Chân trời sáng tạo

Một phân xưởng lắp ráp máy tính dự định lắp ráp x chiếc máy tính cá nhân và y chiếc máy tính bảng trong một ngày. Do hạn chế và nhân công nên mỗi ngày chỉ có thể xuất xưởng tổng hai loại máy tính trên không quá 150 chiếc. Viết hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y

Lời giải:

Vì x và y lần lượt là số chiếc máy tính cá nhân và máy tính bảng mà phân xưởng lắp ráp được trong một ngày nên x ≥ 0, y ≥ 0.

Do hạn chế về nhân công nên mỗi ngày chỉ có thể xuất xưởng tổng hai loại máy tính trên không quá 150 chiếc, do đó x + y ≤ 150.

Vậy ta có hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y là

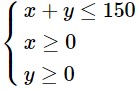
Bài 7 trang 36 SBT Toán 10 - Chân trời sáng tạo

Bạn Hoảng dự dịnh mua x con cá vàng và y con cá Koi từ một trại có giống. Cho biết mỗi con cá vàng có giá 35 nghìn đồng còn mỗi con cá Koi có giá 150 nghìn đồng. Hoàng chỉ để dành được 1,7 triệu dồng và trại cá chỉ bán mỗi loại cá từ 10 con trở lên. Hãy viết hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y

Lời giải:

Vì x và y lần lượt là số cá vàng và cá Koi bạn Hoàng dự định mua và trại cá chỉ bán mỗi loại cá từ 10 con trở lên nên x ≥ 10 và y ≥ 10.

Số tiền mua x con cá vàng là 35x (nghìn đồng).

Số tiền mua y con cá Koi là 150y (nghìn đồng).

Do Hoàng chỉ có 1,7 triệu đồng hay 1700 nghìn đồng nên 35x + 150y ≤ 1700 ⇔ 7x + 30y ≤ 340.

Vậy ta có hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y là

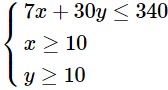
Bài 8 trang 36 SBT Toán 10 - Chân trời sáng tạo

Một học sinh dự dịnh làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ thiện. Cần 1 giờ để làm một bình hoa loại nhỏ và sẽ bán được 100 nghìn đồng, 90 phút để làm một bình hoa loại lớn và sẽ bán được 200 nghìn đồng. Học sinh này chỉ thu xếp được 15 giờ nghỉ để làm và ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa. Hãy chi biết bạn ấy cần làm bao nhiêu bình hoa mỗi loại để gây quỹ được nhiều nhất.

Lời giải:

Gọi x và y lần lượt là số bình hoa loại nhỏ và loại lớn mà bạn học sinh có thể làm được (x ≥ 0, y ≥ 0).

Đổi 90 phút = 1,5 giờ.

Ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa nên x + y ≥ 12.

Số giờ để làm x bình hoa loại nhỏ là x (giờ), số giờ để làm y bình hoa loại lớn là 1,5y (giờ).

Vì học sinh này chỉ thu xếp được 15 giờ nghỉ để làm nên x + 1,5y ≤ 15.

Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tam giác ABC có tọa độ các đỉnh là A(12; 0), B(15; 0), C(6; 6) (phần không gạch chéo kể cả bờ trong hình dưới).

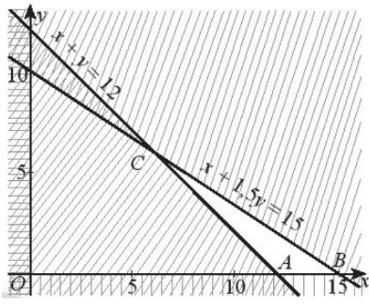
Số tiền gây quỹ là F = 100x + 200y.

Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tam giác ABC.

Ta có: F(12; 0) = 100 . 12 + 200 . 0 = 1 200

F(15; 0) = 100 . 15 + 200 . 0 = 1 500

F(6; 6) = 100 . 6 + 200 . 6 = 1 800.

Do đó, F đạt GTLN là 1 800 nghìn đồng tại đỉnh C(6; 6).

Vậy bạn đó cần làm 6 cái bình hoa mỗi loại để gây được quỹ nhiều tiền nhất.

Bài 9 trang 36 SBT Toán 10 - Chân trời sáng tạo

Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng 6 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 10 triệu. Để sản xuất một tấn sản phẩm Y cần dùng 2 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán được lãi 8 triệu đồng. Hãy lập ké hoạch sản xuất cho xưởng nói trên sao cho  có tổng tiền lãi cao nhất

Lời giải:

Gọi x và y lần lượt là số tấn sản phẩm X và Y mà xưởng cần sản xuất (x ≥ 0, y ≥ 0) (1).

Để sản xuất x tấn sản phẩm X cần 6x tấn nguyên liệu A, 2x tấn nguyên liệu B.

Để sản xuất y tấn sản phẩm Y cần 2y tấn nguyên liệu A, 2y tấn nguyên liệu B.

Do xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B nên 6x + 2y ≤ 12 và 2x + 2y ≤ 8.

Ta có 6x + 2y ≤ 12 ⇔ 3x + y ≤ 6. (2)

2x + 2y ≤ 8 ⇔ x + y ≤ 4. (3)

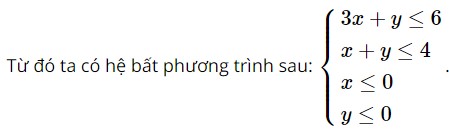
Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tứ giác OABC có tọa độ các đỉnh là: O(0; 0), A(0; 4), B(1; 3), C(2; 0) (miền không bị gạch trong hình sau kể cả bờ).

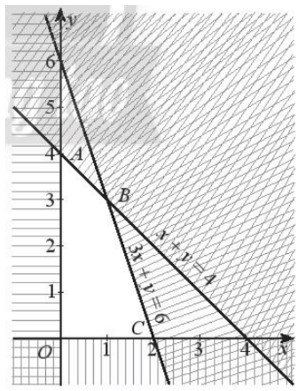
Số tiền lãi khi bán x sản phẩm X và y sản phẩm Y là F = 10x + 8y (triệu đồng).

Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tứ giác OABC.

Ta có: F(0; 0) = 10 . 0 + 8 . 0 = 0

F(0; 4) = 10 . 0 + 8 . 2 = 32

F(1; 3) = 10 . 1 + 8 . 3 = 34

F(2; 0) = 10 . 2 + 8 . 0 = 20

Do đó, F đạt GTLN là 34 triệu đồng tại đỉnh B(1; 3).

Vậy xưởng cần sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y thì sẽ có tổng tiền lãi cao nhất. 

Sachbaitap.com