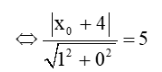Giải SBT Toán 10 trang 46, 47 Kết nối tri thức tập 2
Bài 7.28, 7.29, 7.30, 7.31, 7.32, 7.33, 7.34, 7.35 trang 46, bài 7.36, 7.37 trang 47 SBT Toán 10 KNTT tập 2. Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hành elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cho 2,8 m có thể đi qua hầm được không?
Bài 7.28 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
Cho elip \(\left( E \right)\) có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\). Tìm tiêu điểm và têu cự của elip
Lời giải:
Ta có: \(\left\{ \begin{array}{l}{a^2} = 36\\{b^2} = 16\end{array} \right. \Rightarrow c = \sqrt {{a^2} + {b^2}} = 2\sqrt 5 \)
Vậy \(\left( E \right)\) có hai tiêu điểm là \({F_1}\left( { - 2\sqrt 5 ;0} \right),{F_2}\left( {2\sqrt 5 ;0} \right)\) và có tiêu cự là \(2c = 4\sqrt 5 \)
Bài 7.29 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
Cho hypebol \(\left( H \right)\)có phương trình \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{20}} = 1\). Tìm tiêu điểm và tiêu cự của hypebol
Lời giải:
Trong phương trình chính tắc của \(\left( H \right)\) ta có: \(\left\{ \begin{array}{l}{a^2} = 16\\{b^2} = 20\end{array} \right. \Rightarrow c = \sqrt {{a^2} + {b^2}} = 6\)
Vậy \(\left( H \right)\) có hai tiêu điểm là \({F_1}\left( { - 6;0} \right),{F_2}\left( {6;0} \right)\) và có tiêu cự là \(2c = 12\)
Bài 7.30 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
Cho parabol \(\left( P \right)\) có phương trình \({y^2} = 4x\). Tìm tiêu điểm và đường chuẩn của parabol
Phương pháp:
Parabol \(\left( P \right)\) có dạng \({y^2} = 2px\) với \(p > 0\) có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\), phương trình đường chuẩn \(\Delta :x = - \frac{p}{2}\)
Lời giải:
Dựa vào phương trình chính tắc y2 = 4x của (P) ta có:
2p = 4 ⇔ p = 2 ⇔ p/2 =1.
Vậy (P) có tiêu điểm là F(1; 0) và có đường chuẩn là Δ: x = –1.
Bài 7.31 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
Viết phương trình chính tắc của elip \(\left( E \right)\), biết \(\left( E \right)\) đi qua điểm \(A\left( {6;0} \right)\) và có tiêu cực bằng 8
Lời giải:
+ Vì \(\left( E \right)\) đi qua điểm \(A\left( {6;0} \right)\) nên ta có \(\frac{{{6^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Rightarrow a = 6\)
+ \(\left( E \right)\) có tiêu cự là \(2c = 8\) nên ta có \(c = 4 \Rightarrow {b^2} = {a^2} - {c^2} = {6^2} - {4^2} = 20\)
+ Phương trình chính tắc \(\left( E \right):\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{20}} = 1\)
Bài 7.32 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
Viết phương trình chính tắc của hypebol \(\left( H \right)\), biết \(\left( H \right)\) đi qua điểm \(M\left( {3\sqrt 2 ; - 4} \right)\) và có một tiêu điểm \({F_2}\left( {5;0} \right)\)
Lời giải;
+ Phương trình chính tắc của \(\left( H \right)\) có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\)
+ Do \(\left( H \right)\) có 1 tiêu điểm \({F_2}\left( {5;0} \right)\) nên ta có: \(c = 5 \Rightarrow {a^2} + {b^2} = {c^2} = 25 \Rightarrow {a^2} = 25 - {b^2}\)
+ \(\left( H \right)\) đi qua \(M\left( {3\sqrt 2 ;4} \right)\) nên ta có: \(\frac{{{{\left( {3\sqrt 2 } \right)}^2}}}{{{a^2}}} - \frac{{{4^2}}}{{{b^2}}} = 1 \Rightarrow \frac{{18}}{{{a^2}}} - \frac{{16}}{{{b^2}}} = 1\)
+ Đặt \(t = {b^2} > 0 \Rightarrow {a^2} = 25 - t\)
\(\begin{array}{l} \Rightarrow \frac{{18}}{{25 - t}} - \frac{{16}}{t} = 1 \Rightarrow 18t - 16\left( {25 - t} \right) = t\left( {25 - t} \right)\\ \Rightarrow {t^2} + 9t - 400 = 0 \Rightarrow \left[ \begin{array}{l}t = 16\left( {TM} \right)\\t = - 25\left( L \right)\end{array} \right.\end{array}\)
\( \Rightarrow {b^2} = t = 16,{a^2} = 25 - t = 9\)
Vậy phương trình chính tắc của \(\left( H \right)\) là: \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{25}} = 1\)
Bài 7.33 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
Viết phương trình chính tắc của parabol \(\left( P \right)\), biết rằng \(\left( P \right)\) có đường chuẩn là đường thẳng \(\Delta :x + 4 = 0\). Tìm tọa độ điểm M thuộc \(\left( P \right)\) sao cho khoảng cách từ M đến tiêu điểm của \(\left( P \right)\) bằng 5
Lời giải:
Phương trình chính tắc của (P) có dạng y2 = 2px, trong đó p > 0.
Vì (P) có đường chuẩn là Δ: x + 4 = 0 ⇔ x = –4 ⇔ –p : 2 = –4 ⇔ p = 8
Vậy phương trình chính tắc của (P) là y2 = 16x.
Gọi M (x0; y0).
Vì M thuộc (P) nên ta có:
d(M, Δ) = MF = 5 với F là tiêu điểm của (P) và F(4; 0).
⇔ |x0 + 4| = 5 (*)
TH1: x0 + 4 ≥ 0 hay x0 ≥ –4
(*) ⇔ x0 + 4 = 5 ⇔ x0 = 1 (thỏa mãn)
TH2: x0 + 4 < 0 hay x0 < –4
(*) ⇔ –x0 – 4 = 5 ⇔ x0 = –9 (thỏa mãn)
Với x0 = –9, thay vào phương trình của (P) ta được y02 = 16.(–9) = –144 < 0 (không thể tồn tại)
Với x0 = 1, thay vào phương trình của (P) ta được y02 = 16.1 = 16 ⇔ y0 = ±4
Vậy M(1; 4) hoặc M(1; –4).
Bài 7.34 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
Cho parabol \(\left( P \right)\) có phương trình \({y^2} = 16x\). Gọi \(\Delta \) là đường thẳng bất kì đi qua tiêu điểm F của \(\left( P \right)\) và không trùng với trục hoành. Chứng minh rằng \(\Delta \) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi
Lời giải:
Gọi vecto chỉ phương của \(\Delta \) là \(\overrightarrow {{u_\Delta }} = \left( {a;b} \right)\). Vì \(\Delta \) đi qua điểm \(F\left( {4;0} \right)\) và \(\Delta \) không trùng với trục \(Ox\) nên ta có \(b \ne 0\). Phương trình tham số của \(\Delta \):
\(\left\{ \begin{array}{l}x = 4 + at\\y = 0 + bt = bt\end{array} \right.\)
+ \(\Delta \cap \left( P \right) \Rightarrow {\left( {bt} \right)^2} = 16\left( {4 + at} \right) \Rightarrow {b^2}{t^2} - 16at - 64 = 0\)
+ Phương trình (1) có \(\Delta ' = 64{a^2} + 64{b^2} > 0\) (do \(b \ne 0\)) suy ra phương trình (1) luôn có 2 nghiệm phân biệt. Vậy \(\Delta \) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt A, B
+ Gọi \(A\left( {4 + a{t_1};bt{ & _1}} \right),B\left( {4 + a{t_2};b{t_2}} \right)\) trong đó \({t_1},{t_2}\) là hai nghiệm của phương trình (1). Ta có: \(d\left( {A,Ox} \right).d\left( {B,Ox} \right) = \frac{{\left| {b{t_1}} \right|}}{{\sqrt {{0^2} + {1^2}} }}.\frac{{\left| {b{t_2}} \right|}}{{\sqrt {{0^2} + {1^2}} }} = \left| {{b^2}{t_1}{t_2}} \right|\)
+ Theo định lí Vi-ét, ta có \({t_1}{t_2} = \frac{{ - 64}}{{{b^2}}} \Rightarrow d\left( {A,Ox} \right).d\left( {B,Ox} \right) = \left| {{b^2}.\frac{{ - 64}}{{{b^2}}}} \right| = 64\)
\( \Rightarrow \) Tích các khoảng cách từ A và B đến trục hoành không đổi
Bài 7.35 trang 46 SBT Toán 10 tập 2 Kết nối tri thức
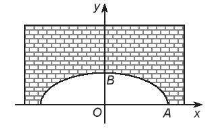
Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hành elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cho 2,8 m có thể đi qua hầm được không?
Phương pháp:
Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\)và có tiêu cự là \(2c\) với \(c = \sqrt {{a^2} - {b^2}} \)
Lời giải:
+ Phương trình chính tắc của \(\left( E \right)\) là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\). Do các điểm \(B\left( {0;3} \right)\) và \(A\left( {6;0} \right)\) thuộc \(\left( E \right)\) nên thay vào phương trình của \(\left( E \right)\) ta có \(b = 3,a = 6\)
\( \Rightarrow \frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\)
+ Với những xe tải có chiều cao 2,8 m, chiều rộng của xe tải là 3 m, tương ứng với \(x = 1,5\). Thay vào phương trình của elip để ta tìm ra độ co của \(y\) của điểm \(M\) (có hoành bộ bằng 1,5 thuộc \(\left( E \right)\)) so với trục \(Ox\):
\({y_M} = 3\sqrt {1 - \frac{{x_M^2}}{{16}}} = 3\sqrt {1 - \frac{{1,{5^2}}}{{16}}} = 2,905 > 2,8\)
\( \Rightarrow \) Ô tô tải có thể đi được qua hầm, tuy nhiên cần khuyến cáo các ô tô phải đi vào chính giữa hầm.
Bài 7.36 trang 47 SBT Toán 10 tập 2 Kết nối tri thức
Cho điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc elip \(\left( E \right)\) có phương trình \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1\)
a) Tính \(M{F_1}^2 - M{F_2}^2\) theo \({x_0};{y_0}\). Từ đó tính \(M{F_1}^2 - M{F_2}^2\) theo \({x_0};{y_0}\)
b) Tìm điểm M sao cho \(M{F_2} = 2M{F_1}\)
c) Tìm M sao cho góc nhìn của M tới hai điểm \({F_1},{F_2}\) (tức là góc \(\widehat {{F_1}M{F_2}}\)) là lớn nhất?
Lời giải:
+ Trong phương trình chính tắc của \(\left( E \right)\) ta có \(a = \sqrt 2 ,b = 1,c = \sqrt {{a^2} - {b^2}} = 1\) và hai tiêu điểm \({F_1}\left( { - 1;0} \right),{F_2}\left( {1;0} \right)\)
a) Ta có \(M{F_1}^2 - M{F_2}^2 = {\left( {{x_0} + 1} \right)^2} + {y_0}^2 - \left[ {{{\left( {{x_0} + 1} \right)}^2} + {y_0}^2} \right] = 4{x_0}\)
+ Ta có \(M \in \left( E \right) \Rightarrow M{F_1} + M{F_2} = 2a = 2\sqrt 2 \) (1)
\( \Rightarrow M{F_1} - M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1}^2 + M{F_2}^2}} = \frac{{4{x_0}}}{{2\sqrt 2 }} = \sqrt 2 {x_0}\) (2)
Từ (1) và (2) suy ra \(\left\{ \begin{array}{l}M{F_1} = \sqrt 2 + \frac{{{x_0}}}{{\sqrt 2 }}\\M{F_2} = \sqrt 2 - \frac{{{x_0}}}{{\sqrt 2 }}\end{array} \right.\)
b) Ta có: \(M{F_2} = 2M{F_1} \Rightarrow \sqrt 2 - \frac{{{x_0}}}{{\sqrt 2 }} = 2\left( {\sqrt 2 + \frac{{{x_0}}}{{\sqrt 2 }}} \right) \Rightarrow \frac{{3{x_0}}}{{\sqrt 2 }} = - \sqrt 2 \Rightarrow {x_0} = - \frac{2}{3}\)
= \(M \in \left( E \right) \Rightarrow \frac{{{x_0}^2}}{2} + \frac{{{y_0}^2}}{1} \Rightarrow {y_0}^2 = 1 - \frac{{{x_0}^2}}{2} = 1 - \frac{{{{\left( { - \frac{2}{3}} \right)}^2}}}{2} = \frac{7}{9} \Rightarrow \left\{ \begin{array}{l}{y_0} = \frac{{\sqrt 7 }}{3}\\{y_0} = - \frac{{\sqrt 7 }}{3}\end{array} \right.\)
Vậy \(M\left( { - \frac{2}{3};\frac{{\sqrt 7 }}{3}} \right)\) hoặc \(M\left( { - \frac{2}{3}; - \frac{{\sqrt 7 }}{3}} \right)\)
c) Áp dụng định lý cosin trong tam giác \(M{F_1}{F_2}\):
\(cos\widehat {{F_1}M{F_2}} = \frac{{M{F_1}^2 + M{F_2}^2 - {F_1}^2{F_2}^2}}{{2M{F_1}.M{F_2}}} = \frac{{{{\left( {\sqrt 2 + \frac{{{x_0}}}{{\sqrt 2 }}} \right)}^2} + {{\left( {\sqrt 2 - \frac{{{x_0}}}{{\sqrt 2 }}} \right)}^2} - {2^2}}}{{2\left( {\sqrt 2 + \frac{{{x_0}}}{{\sqrt 2 }}} \right)\left( {\sqrt 2 - \frac{{{x_0}}}{{\sqrt 2 }}} \right)}} = \frac{{{x_0}^2}}{{4 - {x_0}^2}}\)
+ Ta cos: \(\frac{{{x_0}^2}}{2} = 1 - {y_0}^2 \le 1 \Rightarrow 0 \le {x_0}^2 \le 2\)
\( \Rightarrow cos\widehat {{F_1}M{F_2}} \ge 0 \Rightarrow \widehat {{F_1}M{F_2}} \le {90^ \circ }\)
Dấu “=” xảy ra khi \({x_0} = 0 \Rightarrow {y_0} = \pm 1\)
Bài 7.37 trang 47 SBT Toán 10 tập 2 Kết nối tri thức
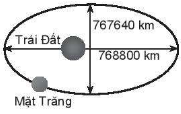
Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm Trái Đất đến Mặt Trăng.
Lời giải:
+ Vì \(2a = 768800\) và \(2b = 767640\) nên ta có \(a = 384400,b = 383820\)
\( \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{{384400}^2} - {{383820}^2}} = 21108\)
\( \Rightarrow \) Khoảng cách lớn nhất từ tâm của Trái Đất đến Mặt Trang là \(a + c = 383400 + 21108 = 405508\) (km)
Và khoảng cách nhỏ nhất là: \(a - c = 383400 - 21108 = 363292\) (km)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SBT Toán 10 trang 70, 71, 72, 73 Kết nối tri thức tập 2 (16/11)
- Giải SBT Toán 10 trang 67, 68, 69 Kết nối tri thức tập 2 (27/02)
- Giải SBT Toán 10 trang 66 Kết nối tri thức tập 2 (27/02)
- Giải SBT Toán 10 trang 63 Kết nối tri thức tập 2 (27/02)
- Giải SBT Toán 10 trang 58, 59, 60 Kết nối tri thức tập 2 (27/02)
- Bài tập cuối chương 9
- Bài 27. Thực hành tính xác suất theo định nghĩa cổ điển
- Bài 26. Biến cố và định nghĩa cổ điển của xác suất
- CHƯƠNG 9. TÍNH XÁC SUẤT THEO ĐỊNH NGHĨA CỔ ĐIỂN
- Bài tập cuối chương 8
- Bài 25. Nhị thức Newton
- Bài 24. Hoán vị, chỉnh hợp và tổ hợp
- Bài 23. Quy tắc đếm
- CHƯƠNG 8. ĐẠI SỐ TỔ HỢP
- Bài tập cuối chương 7
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!