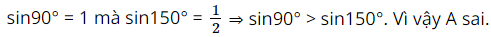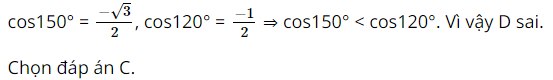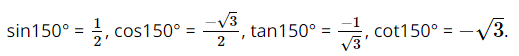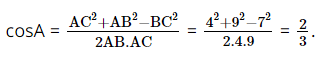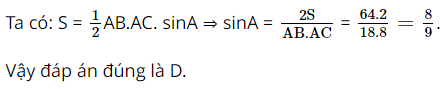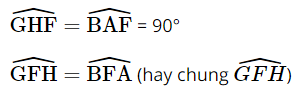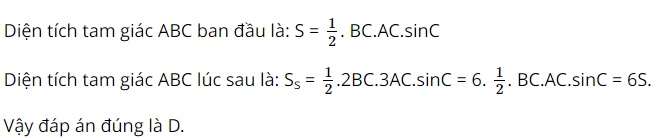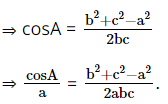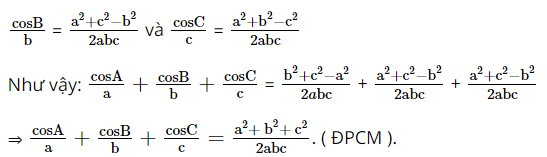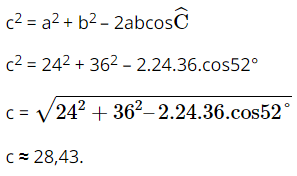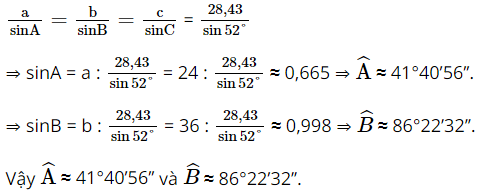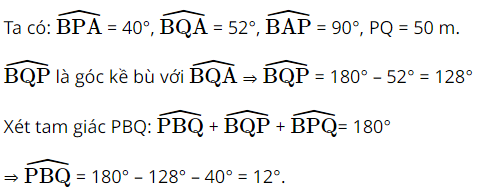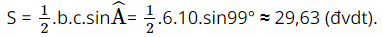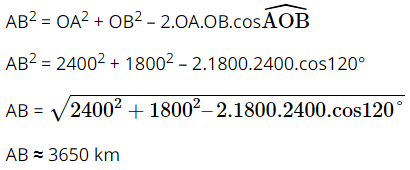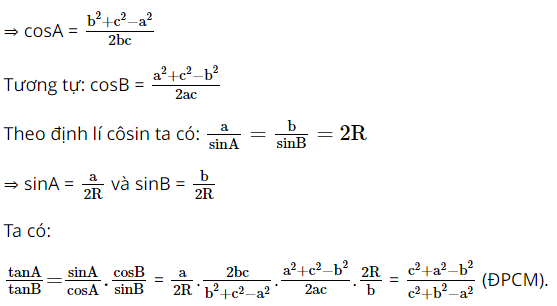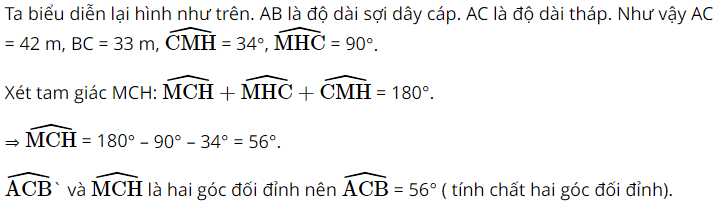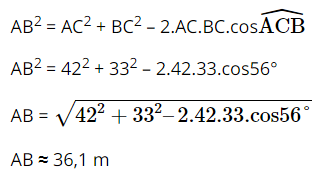Giải SBT Toán 10 trang 80, 81 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 80 bài 9, 10 trang 81 bài 1, 2, 3, 4, 5, 6, 7 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 1. Khẳng định nào sau đây là đúng?
A. TRẮC NGHIỆM
Bài 1 trang 80 SBT Toán 10 - Chân trời sáng tạo
Khẳng định nào sau đây là đúng?
A. \(\sin \alpha = \sin \left( {180^\circ - \alpha } \right)\)
B. \(\cos \alpha = \cos \left( {180^\circ - \alpha } \right)\)
C. \(\tan \alpha = \tan \left( {180^\circ - \alpha } \right)\)
D. \(\cot \alpha = \cot \left( {180^\circ - \alpha } \right)\)
Lời giải:
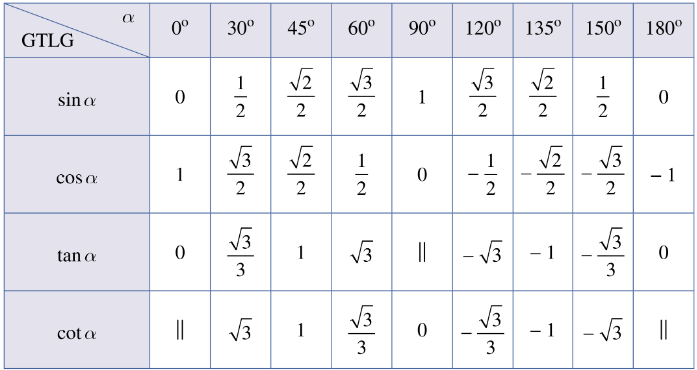
Ta có sin của hai góc bù nhau thì bằng nhau. Côsin, tan và côtan của hai góc bù nhau thì đối nhau. Vậy khẳng định đúng là A.
Bài 2 trang 80 SBT Toán 10 - Chân trời sáng tạo
Trong các khẳng định sau đây, khẳng định nào sai?
A. \(\cos 45^\circ = \sin 45^\circ \)
B. \(\cos 45^\circ = \sin 135^\circ \)
C. \(\cos 30^\circ = \sin 120^\circ \)
D. \(\sin 60^\circ = \cos 120^\circ \)
Phuơng pháp:
\(\cos \alpha = - \cos \left( {180^\circ - \alpha } \right)\)
\(\cos \alpha = \sin \left( {90^\circ - \alpha } \right)\)
Lời giải:
cos45° = sin( 90° – 45° ) = sin45°. Khẳng định A đúng.
cos45° = sin( 90° – 45° ) = sin45° = sin ( 180° – 45° ) = sin135°. Khẳng định B đúng.
cos30° = sin ( 90° – 30° ) = sin60° = sin ( 180° – 60° ) = sin120°. Khẳng định C đúng.
Có sin60° = cos30° ≠ cos120°. Khẳng định D sai.
Vậy chọn đáp án D.
Bài 3 trang 80 SBT Toán 10 - Chân trời sáng tạo
Bất đẳng thức nào sau đây là bất đẳng thức đúng?
A. \(\sin 90^\circ < \sin 150^\circ \)
B. \(\sin 90^\circ 15' < \sin 90^\circ 30'\)
C. \(\sin 90^\circ 30' > \cos 100^\circ \)
D. \(\cos 150^\circ > \cos 120^\circ \)
Lời giải:
Ta có:
sin90°15’ = 0,99999, sin90°30’ = 0,99996 ⇒ sin90°15’ > sin90°30’. Vì vậy B sai.
cos90°30’ ≈ – 8,72. 10-3 , cos100° ≈ – 0,17 ⇒ cos90°30’ > cos100°. Vì vậy C đúng.
Bài 4 trang 80 SBT Toán 10 - Chân trời sáng tạo
Trong các đẳng thức sau đây đẳng thức nào đúng?
A. \(\sin 150^\circ = - \frac{{\sqrt 3 }}{2}\)
B. \(\cos 150^\circ = \frac{{\sqrt 3 }}{2}\)
C. \(\tan 150^\circ = - \frac{1}{{\sqrt 3 }}\)
D. \(\cot 150^\circ = \sqrt 3 \)
Phương pháp:
Lời giải:
Sử dụng máy tính cầm tay ta tính được
Vậy khẳng định C đúng.
Bài 5 trang 80 SBT Toán 10 - Chân trời sáng tạo
Cho tam giác ABC có \(BC = a,CA = b,AB = c\). Mệnh đề nào sau đây đúng?
A. Nếu \({b^2} + {c^2} - {a^2} > 0\) thì góc A nhọn
B. Nếu \({b^2} + {c^2} - {a^2} > 0\) thì góc A tù
C. Nếu \({b^2} + {c^2} - {a^2} < 0\) thì góc A nhọn
D. Nếu \({b^2} + {c^2} - {a^2} < 0\) thì góc A vuông
Lời giải:
Theo định lí côsin ta có: a2 = b2 + c2 – 2bccosA
Bài 6 trang 80 SBT Toán 10 - Chân trời sáng tạo
Cho tam giác ABC có \(AB = 4\) cm, \(BC = 7\) cm, \(CA = 9\). Giá trị \(\cos A\) là
A. \(\frac{2}{3}\)
B. \(\frac{1}{3}\)
C. \(\frac{4}{5}\)
D. \(\frac{8}{9}\)
Lời giải:
Áp dụng hệ quả định lí côsin ta có:
Vậy chọn đáp án A.
Bài 7 trang 80 SBT Toán 10 - Chân trời sáng tạo
Cho tam giác ABC có \(AB = 8\) cm, \(AC = 18\) cm và có diện tích bằng 64 cm2. Giá trị \(\sin A\) là:
A. \(\frac{{\sqrt 3 }}{2}\)
B. \(\frac{3}{8}\)
C. \(\frac{4}{5}\)
D. \(\frac{8}{9}\)
Lời giải:
Bài 8 trang 80 SBT Toán 10 - Chân trời sáng tạo
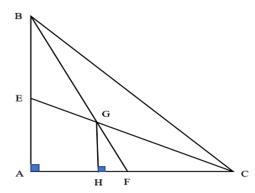
Cho tam giác ABC vuông cân tại A có \(AB = AC = 30\) cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích của tam giác GFC là:
A. 50 \(cm^2\)
B. \(50\sqrt 2 \) \(cm^2\)
C. 75 \(cm^2\)
D.\(15\sqrt {105} \) \(cm^2\)
Lời giải:
Kẻ GH vuông góc với AC.
Xét tam giác GFH và tam giác BFA:
⇒ tam giác GFH và tam giác BFA đồng dạng (g.g)
Vậy đáp án C đúng.
Bài 9 trang 81 SBT Toán 10 - Chân trời sáng tạo
Tam giác ABC có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
A. 2S
B. 3S
C. 4S
D. 6S
Lời giải:
Bài 10 trang 81 SBT Toán 10 - Chân trời sáng tạo
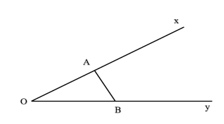
Cho \(\widehat {xOy} = 30^\circ \). Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho \(AB = 1\). Độ dài lớn nhất của đoạn OB bằng:
A. 1,5
B. \(\sqrt 3 \)
C. \(2\sqrt 2 \)
D. 2
Phương pháp:
Áp dụng định lí sin trong tam giác OAB để tính OB.
Lời giải:
Theo định lí sin ta có:
Đáp án đúng là D.
B. TỰ LUẬN
Bài 1 trang 81 SBT Toán 10 - Chân trời sáng tạo
Cho tam giác ABC với ba cạnh a, b, c. Chứng minh rằng:
\(\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c} = \frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}\)
Lời giải:
Theo định lí côsin: a2 = b2 + c2 – 2bccosA
Tương tự ta có:
Bài 2 trang 81 SBT Toán 10 - Chân trời sáng tạo
Cho tam giác ABC. Biết \(a = 24,b = 36,\widehat C = 52^\circ \). Tính cạnh c và hai góc \(\widehat A,\widehat B\)
Lời giải:
Áp dụng định lí côsin ta có:
Áp dụng định lí sin ta có:
Bài 3 trang 81 SBT Toán 10 - Chân trời sáng tạo
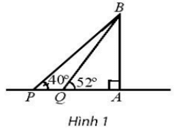
Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = 40^\circ \) và \(\widehat {BQA} = 52^\circ \). Tính chiều cao của tháp hải đăng đó.
Lời giải:
Bài 4 trang 81 SBT Toán 10 - Chân trời sáng tạo
Cho \(\Delta ABC\) có \(\widehat A = 99^\circ ,b = 6,c = 10\). Tính:
a) Diện tích tam giác ABC
b) Bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC
Lời giải:
a) Diện tích tam giác ABC là:
Vậy diện tích tam giác ABC là 29,63 đvdt.
b) Áp dụng định lí côsin ta có:
a2 = b2 + c2 – 2bccosA
a2 = 62 + 102 – 2.6.10.cos99°
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 6,30 và bán kính đường tròn nội tiếp tam giác ABC là 2,08.
Bài 5 trang 81 SBT Toán 10 - Chân trời sáng tạo
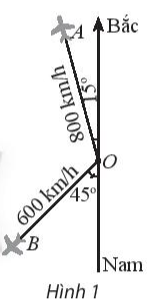
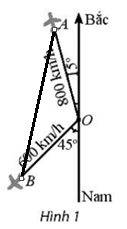
Hai máy bay rời một sân bay cùng một lúc. Một chiếc máy bay với vận tốc 800 km/h theo hướng lệch so với hướng bắc \(15^\circ \) về hướng tây. Chiếc còn lại bay theo hướng lệch so với hướng nam \(45^\circ \) về phía tây với vận tốc 600 km/h (hình 1). Hỏi hai máy bay đó cách nhau bao xa sau 3 giờ?
Lời giải:
Ta có hình vẽ sau:
Sau 3 giờ hai máy bay bay từ O đến A đi được quãng đường là: 800.3 = 2400 km.
Hay OA = 2 400.
Sau 3 giờ hai máy bay bay từ O đến B đi được quãng đường là: 600.3 = 1 800 km.
Hay OB = 1 800.
Sau 3 giờ, hai máy bay A, B và điểm xuất phát O tạo thành tam giác OAB với OA = 2400 và OB = 1800. Áp dụng định lí côsin cho tam giác OAB ta được:
Vậy sau 3 giờ hai máy bay cách nhau khoảng 3650 km.
Bài 6 trang 81 SBT Toán 10 - Chân trời sáng tạo
Cho tam giác ABC không vuông. Chứng minh rằng: \(\frac{{\tan A}}{{\tan B}} = \frac{{{c^2} + {a^2} - {b^2}}}{{{c^2} + {b^2} - {a^2}}}\)
Lời giải:
Theo định lí côsin ta có: a2 = b2 + c2 – 2bcosA
Bài 7 trang 81 SBT Toán 10 - Chân trời sáng tạo
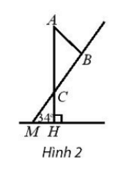
Một tháp viễn thông cao 42m được dựng thẳng đứng trên một sườn dốc \(34^\circ \)so với phương ngang. Từ đỉnh tháp người ta neo một sợi dây cáp xuống một điểm trên sườn dốc cách chân tháp 33 m như hình 2. Tính chiều dài của sợi dây đó.
Lời gải:
Áp dụng định lí côsin cho tam giác ABC:
Vậy chiều dài sợi dây cáp khoảng 36,1 m.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SBT Toán 10 trang 102, 103 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 100, 101 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 95, 96, 97 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 77, 78, 79, 80 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 75, 76 Chân trời sáng tạo tập 2 (30/01)
- Bài tập cuối chương X - SBT Toán 10 CTST
- Bài 2. Xác suất của biến cố - SBT Toán 10 CTST
- Bài 1. Không gian mẫu và biến cố - SBT Toán 10 CTST
- Chương X. Xác suất - SBT Toán 10 CTST
- Bài tập cuối chương IX - SBT Toán 10 CTST
- Bài 4. Ba đường conic trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 3. Đường tròn trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 2. Đường thẳng trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 1. Tọa độ của vectơ - SBT Toán 10 CTST
- Chương IX. Phương pháp tọa độ trong mặt phẳng - SBT Toán 10 CTST
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!