Giải SGK Toán 11 Kết nối tri thức tập 2 trang 9
Giải bài 6.1, 6.2, 6.3, 6.4, 6.5, 6.6, 6.7, 6.8 trang 9 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Nếu một khoản tiền gốc P được gửi ngân hàng với lãi suất hằng năm r (được biểu thị dưới dạng số thập phân), được tính lãi n lần trong một năm, thì tổng số tiền A nhận được (cả vốn lẫn lãi) sau N kì gửi cho bởi công thức sau:
Bài 6.1 trang 9 SGK Toán 11 - Kết Nối Tri Thức tập 2
Tính:
a) \({\left( {\frac{1}{5}} \right)^{ - 2}};\)
b) \({4^{\frac{3}{2}}};\)
c) \({\left( {\frac{1}{8}} \right)^{ - \frac{2}{3}}};\)
d) \({\left( {\frac{1}{{16}}} \right)^{ - 0,75}}.\)
Phương pháp:
Sử dụng máy tính cầm tay.
Lời giải:
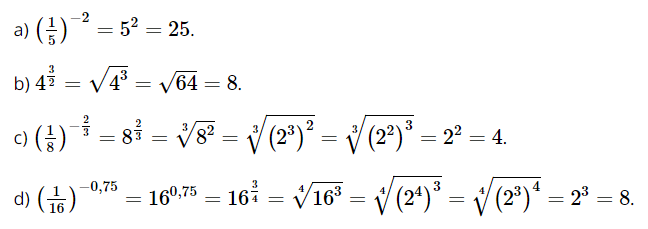
Bài 6.2 trang 9 SGK Toán 11 - Kết Nối Tri Thức tập 2
Thực hiện phép tính:
a) \({27^{\frac{2}{3}}} + {81^{ - 0,75}} - {25^{0,5}};\)
b) \({4^{2 - 3\sqrt 7 }}{.8^{2\sqrt 7 }}.\)
Phương pháp:
Sử dụng các công thức
\({a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}};a = \sqrt[n]{{{a^n}}};{\left( {{a^m}} \right)^n} = {a^{m.n}};{a^m}.{a^n} = {a^{m + n}}.\)
Lời giải:
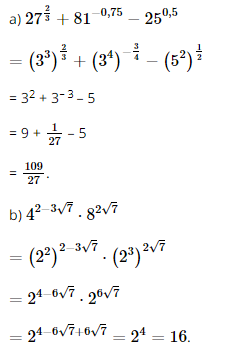
Bài 6.3 trang 9 SGK Toán 11 - Kết Nối Tri Thức tập 2
Rút gọn các biểu thức sau:
a) \(A = \frac{{{x^5}{y^{ - 2}}}}{{{x^3}y}}\,\,\,\left( {x,y \ne 0} \right);\)
b) \(B = \frac{{{x^2}{y^{ - 3}}}}{{{{\left( {{x^{ - 1}}{y^4}} \right)}^{ - 3}}}}\,\,\,\left( {x,y \ne 0} \right).\)
Phương pháp:
Sử dụng các công thức \({a^m}:{a^n} = {a^{m - n}};{\left( {ab} \right)^n} = {a^n}.{b^n}.\)
Lời giải:
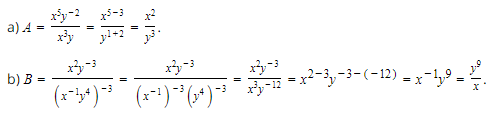
Bài 6.4 trang 9 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho x, y là các số thực dương. Rút gọn các biểu thức sau:
a) \(A = \frac{{{x^{\frac{1}{3}}}\sqrt y + {y^{\frac{1}{3}}}\sqrt x }}{{\sqrt[6]{x} + \sqrt[6]{y}}};\)
b) \(B = {\left( {\frac{{{x^{\sqrt 3 }}}}{{{y^{\sqrt 3 - 1}}}}} \right)^{\sqrt 3 + 1}}.\frac{{{x^{ - \sqrt 3 - 1}}}}{{{y^{ - 2}}}}.\)
Phương pháp:
Sử dụng công thức
\({a^{\frac{1}{n}}} = \sqrt[n]{a};{\left( {{a^m}} \right)^n} = {a^{m.n}};{a^m}:{a^n} = {a^{m - n}};{a^{ - n}} = \frac{1}{{{a^n}}}.\)
Lời giải:
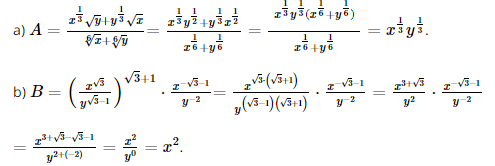
Bài 6.5 trang 9 SGK Toán 11 - Kết Nối Tri Thức tập 2
Chứng minh rằng \(\sqrt {4 + 2\sqrt 3 } - \sqrt {4 - 2\sqrt 3 } = 2.\)
Phương pháp:
Sử dụng hằng đẳng thức bậc 2 để biến đổi biểu thức dưới dấu căn và áp dụng công thức \(\sqrt {{a^2}} = a\,\,\left( {a > 0} \right)\)
Lời giải:
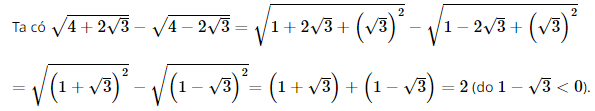
Bài 6.6 trang 9 SGK Toán 11 - Kết Nối Tri Thức tập 2
Không sử dụng máy tính cầm tay, hãy so sánh:
a) \({5^{6\sqrt 3 }}\) và \({5^{3\sqrt 6 }};\)
b) \({\left( {\frac{1}{2}} \right)^{ - \frac{4}{3}}}\) và \(\sqrt 2 {.2^{\frac{2}{3}}}.\)
Phương pháp:
Đưa về so sánh 2 lũy thừa cùng cơ số.
Lời giải:
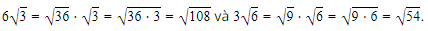

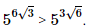
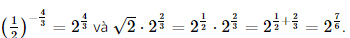
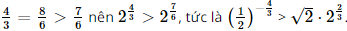
Bài 6.7 trang 9 SGK Toán 11 - Kết Nối Tri Thức tập 2
Nếu một khoản tiền gốc P được gửi ngân hàng với lãi suất hằng năm r (r được biểu thị dưới dạng số thập phân), được tính lãi n lần trong một năm, thì tổng số tiền A nhận được (cả vốn lẫn lãi) sau N kì gửi cho bởi công thức sau:
\(A = P{\left( {1 + \frac{r}{n}} \right)^N}.\)
Hỏi nếu bác An gửi tiết kiệm số tiền 120 triệu đồng theo kì hạn 6 tháng với lãi suất không đổi là 5% một năm, thì số tiền thu được (cả vốn lẫn lãi) của bác An sau 2 năm là bao nhiêu?
Phương pháp:
Áp dụng công thức và bấm máy tính.
Lời giải:
Ta có P = 120, r = 5% = 0,05.
Vậy số tiền bác An thu được (cả vốn lẫn lãi) sau 2 năm là
120. 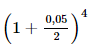 ≈132,46 (triệu đồng).
≈132,46 (triệu đồng).
Phương pháp:
Áp dụng công thức và bấm máy tính.
Lời giải:
Thay t = 20 vào công thức A=19⋅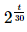 ta được
ta được
A=19⋅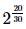 ≈30 (triệu người).
≈30 (triệu người).
Vậy sau 20 năm nữa kể từ năm 2021, dân số của quốc gia đó là khoảng 30 triệu người.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 107, 108, 109 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 105, 106 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 99, 100, 101 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 97 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 96 (11/01)
- BÀI TẬP ÔN TẬP CUỐI CUỐI NĂM
- Hoạt động thực hành trải nghiệm Hình học
- HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
- Bài tập cuối chương 9
- Bài 33. Đạo hàm cấp hai
- Bài 32. Các quy tắc tính đạo hàm
- Bài 31. Định nghĩa và ý nghĩa của đạo hàm
- CHƯƠNG IX. ĐẠO HÀM
- Bài tập cuối chương 8
- Bài 30. Công thức nhân xác suất cho hai biến cố độc lập
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
