Giải SGK Toán 12 tập 2 Chân trời sáng tạo trang 20
Giải bài 1, 2, 3, 4, 5, 6 trang 20 SGK Toán 12 Chân trời sáng tạo tập 2. Tính diện tích hình thang cong giới hạn bởi: a) Đồ thị hàm số \(y = {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\).
Bài 1 trang 20 SGK Toán 12 Tập 2 Chân trời sáng tạo
Tính diện tích hình thang cong giới hạn bởi:
a) Đồ thị hàm số \(y = {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\).
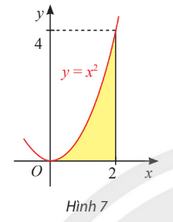
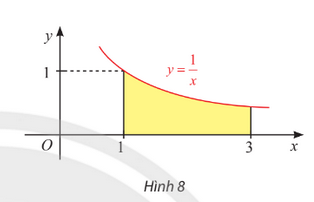
b) Đồ thị hàm số \(y = \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 3\).
Phương pháp:
Diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {f\left( x \right)dx} \).
Lời giải:

Bài 2 trang 20 SGK Toán 12 Tập 2 Chân trời sáng tạo
Tính các tích phân sau:
a) \(\int\limits_1^2 {{x^4}dx} \)
b) \(\int\limits_1^2 {\frac{1}{{\sqrt x }}dx} \)
c) \(\int\limits_0^{\frac{\pi }{4}} {\frac{1}{{{{\cos }^2}x}}dx} \)
d) \(\int\limits_0^2 {{3^x}dx} \)
Phương pháp:
Sử dụng công thức tính tích phân \(\int\limits_a^b {f\left( x \right)dx} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) - F\left( a \right)\).
Lời giải:
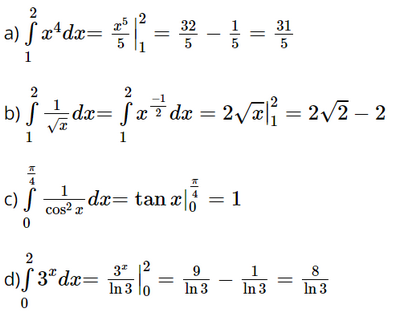
Bài 3 trang 20 SGK Toán 12 Tập 2 Chân trời sáng tạo
Tính các tích phân sau:
a) \(\int\limits_{ - 2}^4 {\left( {x + 1} \right)\left( {x - 1} \right)dx} \)
b) \(\int\limits_1^2 {\frac{{{x^2} - 2x + 1}}{x}dx} \)
c) \(\int\limits_0^{\frac{\pi }{2}} {\left( {3\sin x - 2} \right)dx} \)
d) \(\int\limits_0^{\frac{\pi }{2}} {\frac{{{{\sin }^2}x}}{{1 + \cos x}}dx} \)
Phương pháp:
Sử dụng tính chất tích phân của một tổng, một hiệu để đưa về tính các tích phân đơn giản.
Lời giải:
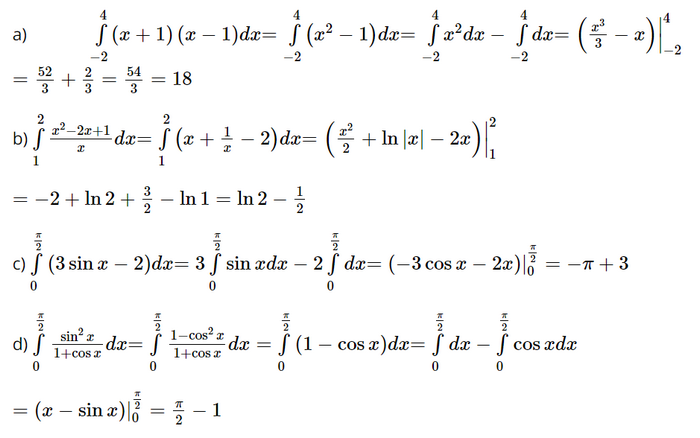
Bài 4 trang 20 SGK Toán 12 Tập 2 Chân trời sáng tạo
Tính các tích phân sau:
a) \(\int\limits_{ - 2}^1 {\left| {2x + 2} \right|dx} \)
b) \(\int\limits_0^4 {\left| {{x^2} - 4} \right|dx} \)
c) \(\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\left| {\sin x} \right|dx} \)
Phương pháp:
Sử dụng tính chất của tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \) để phá dấu giá trị tuyệt đối và đưa về tính các tích phân đơn giản.
Lời giải:
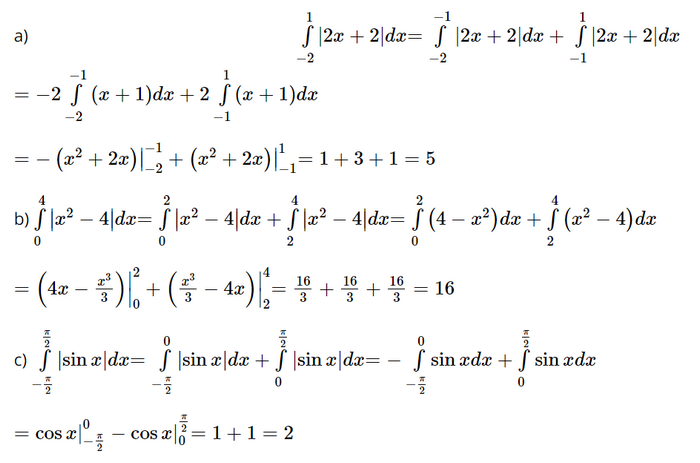
Bài 5 trang 20 SGK Toán 12 Tập 2 Chân trời sáng tạo
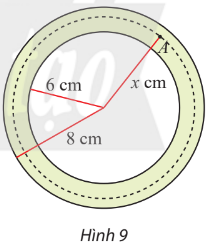
Mặt cắt ngang của một ống dẫn khí nóng là một hình vành khuyên như hình dưới đây. Khí bên trong ống được duy trì ở \({150^o}{\rm{C}}\). Biết rằng nhiệt độ \(T\left( {^oC} \right)\) tại điểm A trên thành ống là hàm số của khoảng cách \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) từ A đến tâm của mặt cắt và \(T'\left( x \right) = - \frac{{30}}{x}\) \(\left( {6 \le x \le 8} \right)\). Tìm nhiệt độ mặt ngoài của ống.
Phương pháp:
Do nhiệt độ của khí bên trong ống luôn được duy trì ở \({150^o}{\rm{C}}\), nên \(T\left( 6 \right) = 150\).
Nhiệt độ mặt ngoài của ống là \(T\left( 8 \right) = \left[ {T\left( 8 \right) - T\left( 6 \right)} \right] + T\left( 6 \right) = \int\limits_6^8 {T'\left( x \right)dx} + T\left( 6 \right)\).
Lời giải:
Nhiệt độ tại điểm A trên thành ống là
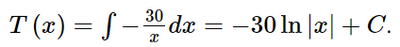
Vì T(6) = 150°C nên −30ln6 + C = 150 => C = 150 + 30ln6.
Do đó T(x) = −30ln|x| + 150 + 30ln6.
Nhiệt độ ngoài mặt ống là T(8) = −30ln8 + 150 + 30ln6 ≈ 141,37°C.
Bài 6 trang 20 SGK Toán 12 Tập 2 Chân trời sáng tạo
Tốc độ \(v{\rm{ }}\left( {{\rm{m/s}}} \right)\) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian \(t\) (giây) được cho bởi công thức \(v\left( t \right) = \left\{ {\begin{array}{*{20}{c}}t&{\left( {0 \le t \le 2} \right)}\\2&{\left( {2 < t \le 20} \right)}\\{12 - 0,5t}&{\left( {20 < t \le 24} \right)}\end{array}} \right.\). Tính quãng đường chuyển động và tốc độ trung bình của thang máy.
Phương pháp:
Gọi \(s\left( t \right)\) là quãng đường thang máy di chuyển được đến thời gian \(t\) (giây).
Quãng đường thang máy di chuyển từ tầng 1 lên tầng cao nhất là \(s = s\left( {24} \right) - s\left( 0 \right) = \int\limits_0^{24} {v\left( t \right)dt} \).
Sử dụng tính chất \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \) để tính tích phân \(\int\limits_0^{24} {v\left( t \right)dt} \).
Vận tốc trung bình của thang máy khi di chuyển từ tầng 1 lên tầng cao nhất là \({v_{tb}} = \frac{s}{t}\)
Lời giải:

Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SGK Toán 12 tập 2 Chân trời sáng tạo trang 27 (29/07)
- Giải SGK Toán 12 tập 2 Chân trời sáng tạo trang 20 (29/07)
- Giải SGK Toán 12 tập 2 Chân trời sáng tạo trang 11, 12 (29/07)
- Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 92, 93 (29/07)
- Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 89 (29/07)
- Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay
- Bài 1: Vẽ đồ thị hàm số bằng phần mềm Geogebra
- Hoạt động thực hành và trải nghiệm
- Bài tập cuối chương 3
- Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm
- Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm
- Chương 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm
- Bài tập cuối chương 2
- Bài 3: Biểu thức toạ độ của các phép toán vectơ
- Bài 2: Toạ độ của vectơ trong không gian
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!