Giải SGK Toán 8 trang 17, 18 Kết nối tri thức tập 1

Bài 1.18 trang 17 SGK Toán 8 tập 1 - Kết nối tri thức

Cho các biểu thức:

\(\dfrac{4}{5}x;\left( {\sqrt 2  - 1} \right)xy; - 3x{y^2};\dfrac{1}{2}{x^2}y;\dfrac{1}{x}{y^3}; - xy + \sqrt 2 ;\dfrac{{ - 3}}{2}{x^2}y;\dfrac{{\sqrt x }}{5}.\)

a)      Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?

b)      Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.

c)      Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.

Phương pháp:

a)      Đơn thức là biểu thức đại số chỉ gồm một số hoặc biến, hoặc tích của những số và biến.

b)      Trong đơn thức thu gọn:

+) Hệ số là phần số.

+) Phần biến là phần còn lại trong đơn thức (không là phần số)

+) Tổng số mũ của các biến trong đơn thức có hệ số khác 0 là bậc của đơn thức.

c)      Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.

Lời giải:

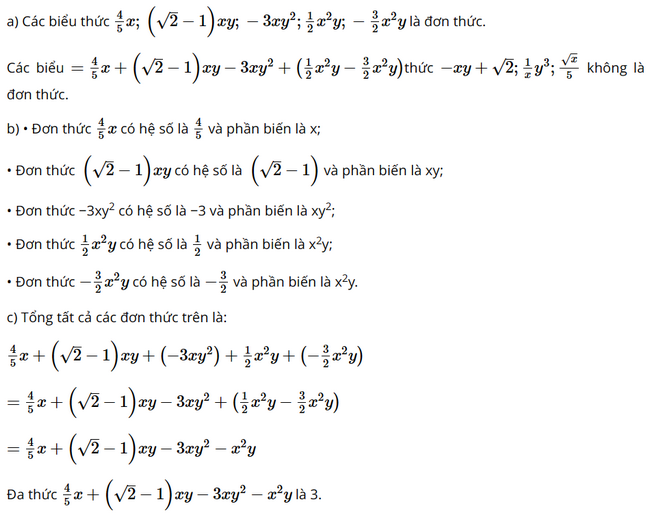
Bài 1.19 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức

Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là 1,2 m, đáy là hình chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ hai có chiều sâu là 1,5 m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.

a)      Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.

b)      Tính lượng nước bơm đầy hai bể nếu x=5 m, y=3 m.

Lời giải:

a)       

\(\begin{array}{l}{V_1} = 1,2.x.y\left( {{m^3}} \right)\\{V_2} = 1,5.5x.5y = 37,5.x.y\left( {{m^3}} \right)\end{array}\)

b)      Biểu thức biểu thị tổng thể tích ở 2 bể là:

\(V = {V_1} + {V_2} = 1,2xy + 37,5xy = \left( {1,2 + 37,5} \right)xy = 38,7xy.\)

Thay x=5, y=3 vào biểu thức V ta được:

\(V = 38,7.5.3 = 580,5\left( {{m^3}} \right)\)

Vậy lượng nước bơm đầy hai bể nếu x=5 m, y=3 m là \(580,5\,{m^3}\).

Bài 1.20 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức

Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x=1;y=-2.

\(\begin{array}{l}P = 5{x^4} - 3{x^3}y + 2x{y^3} - {x^3}y + 2{y^4} - 7{x^2}{y^2} - 2x{y^3};\\Q = {x^3} + {x^2}y + x{y^2} - {x^2}y - x{y^2} - {x^3}.\end{array}\)

Lời giải:

\(\begin{array}{l}P = 5{x^4} - 3{x^3}y + 2x{y^3} - {x^3}y + 2{y^4} - 7{x^2}{y^2} - 2x{y^3}\\ = 5{x^4} + 2{y^4} + \left( { - 3{x^3}y - {x^3}y} \right) + \left( {2x{y^3} - 2x{y^3}} \right) - 7{x^2}{y^2}\\ = 5{x^4} + 2{y^4} - 4{x^3}y - 7{x^2}{y^2}\\Q = {x^3} + {x^2}y + x{y^2} - {x^2}y - x{y^2} - {x^3}\\ = \left( {{x^3} - {x^3}} \right) + \left( {{x^2}y - {x^2}y} \right) + \left( {x{y^2} - x{y^2}} \right)\\ = 0\end{array}\)

Do đó, bậc của đa thức P là 4; đa thức Q không có bậc.

Bài 1.21 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức

Cho hai đa thức:

\(A = 7xy{z^2} - 5x{y^2}z + 3{x^2}yz - xyz + 1;B = 7{x^2}yz - 5x{y^2}z + 3xy{z^2} - 2.\)

a)      Tìm đa thức C sao cho A-C=B;

b)      Tìm đa thức D sao cho A+D=B;

c)      Tìm đa thức E sao cho E-A=B;

Phương pháp:

Sử dụng bài toán ngược tìm C,D,E. Sau đó sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.

Lời giải:

a) Ta có A – C = B

Suy ra C = A – B = (7xyz² – 5xy²z + 3x²yz – xyz + 1) – (7x²yz – 5xy²z + 3xyz² – 2)

= 7xyz² – 5xy²z + 3x²yz – xyz + 1 – 7x²yz + 5xy²z – 3xyz² + 2

= (7xyz² – 3xyz²) + (5xy²z – 5xy²z) + (3x²yz – 7x²yz) – xyz + (1 + 2)

= 4xyz² – 4x²yz – xyz + 3.

Vậy C = 4xyz² – 4x²yz – xyz + 3.

b) Ta có A + D = B

Suy ra D = B – A = –(A – B) = –(4xyz² – 4x²yz – xyz + 3)

= –4xyz² + 4x²yz + xyz – 3.

Vậy D = –4xyz² + 4x²yz + xyz – 3.

c) Ta có E – A = B.

Suy ra E = A + B = (7xyz² – 5xy²z + 3x²yz – xyz + 1) + (7x²yz – 5xy²z + 3xyz² – 2)

= 7xyz² – 5xy²z + 3x²yz – xyz + 1 + 7x²yz – 5xy²z + 3xyz² – 2

= (7xyz² + 3xyz²) – (5xy²z + 5xy²z) + (7x²yz + 3x²yz) – xyz + (1 – 2)

= 10x²yz – 10xy²z + 10xyz² – xyz + 3.

Vậy E = 10x²yz – 10xy²z + 10xyz² – xyz + 3.

Bài 1.22 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức

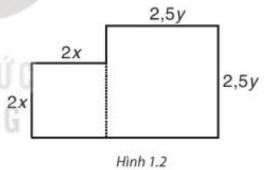
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimet và y centimet. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimet) như Hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?

Phương pháp:

Biểu thị diện tích phần còn lại của miếng bìa: Diện tích phần còn lại = Diện tích 2 hình vuông – Diện tích 2 hình tròn.

Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.

Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.

Lời giải:

Trong Hình 1.2 có:

• Diện tích hình vuông nhỏ là: (2x)² = 4x² (cm²).

Diện tích hình vuông lớn là: (2,5y)² = 6,25y² (cm²).

Tổng diện tích hai hình vuông là: 4x² + 6,25y² (cm²).

• Hình tròn nhỏ có đường kính là 2x nên sẽ có bán kính là x (cm)

Diện tích hình tròn nhỏ là: πx² (cm²).

• Hình tròn lớn có đường kính là 2,5y nên sẽ có bán kính là 1,25y (cm)

Diện tích hình tròn lớn là: 1,5625πy² (cm²).

Do đó, biểu thức biểu thị diện tích phần còn lại của miếng bìa là:

(4x² + 6,25y²) – (πx² + 1,5625πy²) = 4x² + 6,25y² – πx² – 1,5625πy²

= (4x² – πx²) + (6,25y² – 1,5625πy²)

= (4 – π)x² + (6,25 – 1,5625π)y²

Biểu thức (4 – π)x² + (6,25 – 1,5625π)y² là một đa thức bậc 2.

Bài 1.23 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức

Cho ba đa thức:

\(M = 3{x^3} - 4{x^2}y + 3x - y;N = 5xy - 3x + 2;P = 3{x^3} + 2{x^2}y + 7x - 1.\)

Tính M+N-P và M-N-P.

Phương pháp:

Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.

Lời giải:

Ta có:

• M + N – P = (3x³ – 4x²y + 3x – y) + (5xy – 3x + 2) – (3x³ + 2x²y + 7x – 1)

= 3x³ – 4x²y + 3x – y + 5xy – 3x + 2 – 3x³ – 2x²y – 7x + 1

= (3x³ – 3x³) – (4x²y + 2x²y) + 5xy + (3x – 3x – 7x) – y + (2 + 1)

= – 6x²y + 5xy – 7x – y + 3.

• M – N – P = (3x³ – 4x²y + 3x – y) – (5xy – 3x + 2) – (3x³ + 2x²y + 7x – 1)

= 3x³ – 4x²y + 3x – y + 5xy + 3x – 2 – 3x³ – 2x²y – 7x + 1

= (3x³ – 3x³) – (4x²y + 2x²y) + 5xy + (3x + 3x – 7x) – y + (1 – 2)

= – 6x²y + 5xy – x – y – 1.

Vậy M + N – P = – 6x²y + 5xy – 7x – y + 3; M – N – P = – 6x²y + 5xy – x – y – 1.

Sachbaitap.com