Giải SGK Toán 8 trang 51 Kết nối tri thức tập 1
Giải bài 3.1, 3.2, 3.3 trang 51 SGK Toán lớp 8 kết nối tri thức tập 1. Tính góc chưa biết của các tứ giác trong Hình 3.8. Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.
Bài 3.1 trang 51 SGK Toán 8 tập 1 - Kết nối tri thức
Tính góc chưa biết của các tứ giác trong Hình 3.8.
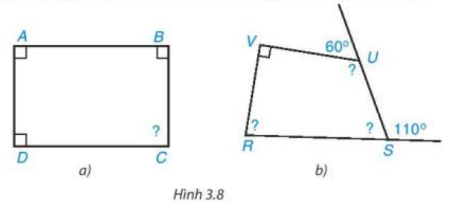
Lời giải:
• Hình 3.8a)
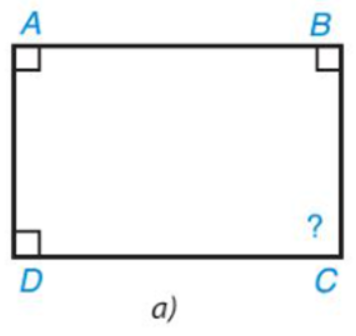
Xét tứ giác ABCD có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Hay 90°+90°+ˆC+90°=360°
Khi đó \(\widehat C\)+270°=360°
Do đó \(\widehat C\)=360°−270°=90°.
Vậy \(\widehat C\)=90°
• Hình 3.8b)
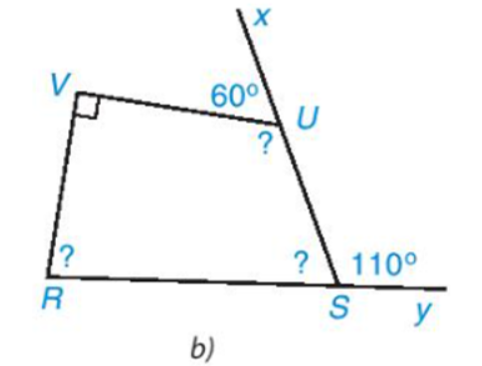
Vì \(\widehat {{\rm{VUS}}}\) và \(\widehat {VUx}\) là hai góc kề bù nên ta có: \(\widehat {{\rm{VUS}}} + \widehat {VUx} = {180^o}\)
Hay \(\widehat {{\rm{VUS}}}\)+60°=180°
Suy ra \(\widehat {{\rm{VUS}}}\)=180°−60°=120°
Vì \(\widehat {US{\rm{R}}}\)và \(\widehat {USy}\)là hai góc kề bù nên ta có: \(\widehat {US{\rm{R}}} + \widehat {USy} = {180^o}\)
Hay \(\widehat {US{\rm{R}}}\)+110°=180o
Suy ra \(\widehat {US{\rm{R}}}\) =180°−110°=70°
Do đó \(\widehat {US{\rm{R}}}\)=70°
Xét tứ giác VUSR có:
\(\widehat V + \widehat {{\rm{VUS}}} + \widehat {V{\rm{SR}}} + \widehat R = {360^o}\)
Hay 90°+120°+70°+\(\widehat R\)=360°
Khi đó 280°+\(\widehat R\)=360°
Do đó \(\widehat R\)=360°−280°=80°
Vậy \(\widehat R\)=80°
Bài 3.2 trang 51 SGK Toán 8 tập 1 - Kết nối tri thức
Tính góc chưa biết của tứ giác trong Hình 3.9. Biết rằng \(\widehat H\)=\(\widehat E\)+10o
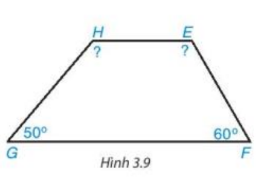
Lời giải:
Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
\(\widehat H + \widehat E + \widehat F + \widehat G = {360^o}\)
\(\widehat E\)+10°+\(\widehat E\)+60°+50°=360o
2\(\widehat E\)+120°=360°
Suy ra 2\(\widehat E\)=360°−120°=240°
Khi đó \(\widehat E\)=120°
Suy ra \(\widehat H\)=\(\widehat E\)+10°=120°+10°=130°
Vậy \(\widehat H\)=130°; \(\widehat E\)=120°
Bài 3.3 trang 51 SGK Toán 8 tập 1 - Kết nối tri thức
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.
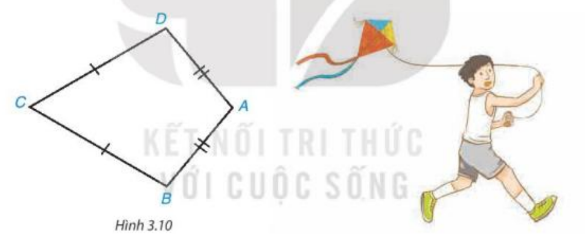
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Tính các góc B, D biết rằng \(\widehat A\)=100°,\(\widehat C\)=60°
Lời giải:
a) Nối AC, BD (như hình vẽ

Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;
CB = CD hay hai điểm C cách đều hai đầu mút B và D;
Do đó, hai điểm A và C cách đều hai đầu mút B và D.
Vậy AC là đường trung trực của đoạn thẳng BD.
b) Gọi I là giao điểm của AC và BD.
Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.
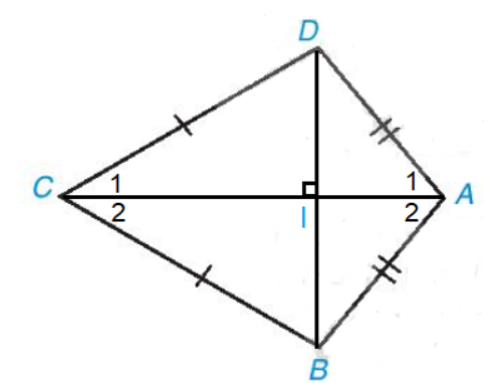
• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)
Nên AI cũng là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay \(\widehat {{A_1}} = \widehat {{A_2}}\)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {B{\rm{D}}A}:2 = {100^o}:2 = {50^o}\)
• Xét tam giác BCD cân tại C (vì BC = CD) có CI là đường cao (vì AC ⊥ BD)
Nên CI cũng là tia phân giác của \(\widehat {BC{\rm{D}}}\) hay \(\widehat {{C_1}} = \widehat {{C_2}}\)
Suy ra \(\widehat {{C_1}} = \widehat {{C_2}} = \widehat {BC{\rm{D}}}:2 = {60^o}:2 = {30^o}\)
• Xét tam giác ACD có: \(\widehat {{A_1}} + \widehat {{C_1}} + \widehat {A{\rm{D}}C} = {180^o}\) (định lí tổng ba góc trong một tam giác).
Hay 50°+30°+\(\widehat {A{\rm{D}}C}\)=180°
Suy ra \(\widehat {A{\rm{D}}C}\)=180°−50°−30°=100°
Xét tứ giác ABCD có:
\(\widehat {BA{\rm{D}}} + \widehat {ABC} + \widehat {BC{\rm{D}}} + \widehat {A{\rm{D}}C} = {360^o}\)(định lí tổng ba góc trong một tam giác).
Hay 100°+\(\widehat {ABC}\)+60°+100°=360°
Suy ra \(\widehat {ABC}\)+260°=360o
Do đó \(\widehat {ABC}\)=360°−260°=100o
Vậy \(\widehat {ABC}\)=100° ;\(\widehat {A{\rm{D}}C}\)=100°
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,15 trang 135,136 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.15, 10.16, 10.17, 10.18, 10.19, 10.20, 10.21, 10.22, 10.23, 10.24 trang 123, 124 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.11, 10.12, 10.13, 10.14 trang 121, 122 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.5, 10.6, 10.7, 10.8, 10.9, 10.10 trang 120 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.1, 10.2, 10.3, 10.4 trang 116 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Bài tập ôn tập cuối năm
- Bài tập cuối chương 10
- Luyện tập chung (trang 121)
- Bài 39. Hình chóp tứ giác đều
- Bài 38. Hình chóp tam giác đều
- CHƯƠNG X. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
- Bài tập cuối chương 9
- Luyện tập chung (trang 108)
- Bài 37.Hình đồng dạng
- Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
