Giải SGK Toán 8 trang 58, 59 Cánh Diều tập 1

Bài 1 trang 58 SGK Toán 8 tập 1 - Cánh Diều

Đại lượng y có phải là hàm số của đại lượng x hay không nếu bảng giá trị tương ứng của chúng được cho bởi mỗi trường hợp sau:

a)

b)

Phương pháp:

Dựa vào định nghĩa hàm số

Lời giải:

a)

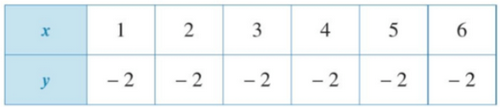
Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 5; x = 6 thì ta đều xác định  giá trị của y là y = − 2.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

b)

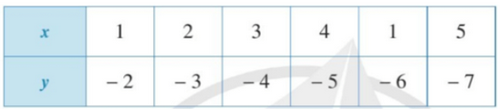
Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 1; x = 5 thì ta đều xác định  giá trị của y lần lượt là: y = − 2; y = − 3; y = − 4; y = − 5; y = − 6; y = − 7.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

Bài 2 trang 58 SGK Toán 8 tập 1 - Cánh Diều

a) Cho hàm số y = 2x + 10. Tìm giá trị của y tương ứng với mỗi giá trị sau của x:

x = -5; x = 0; x = \(\dfrac{1}{2}\)

b) Cho hàm số y = -2x² + 1. Tìm giá trị của y tương ứng với mỗi giá trị sau của x:

x = -1; x = 0; x = 1; x = \(\dfrac{1}{3}\)

Phương pháp:

Thay các giá trị đã cho vào hàm số để tính các giá trị tương ứng.

Lời giải:

a) Thay lần lượt các giá trị x = -5; x = 0; x = \(\dfrac{1}{2}\) vào hàm số y = 2x + 10 ta được bảng giá trị sau:

b) Thay lần lượt các giá trị x = -1; x = 0; x = 1; x = \(\dfrac{1}{3}\) vào hàm số y = -2x² + 1 ta được bảng giá trị sau:

Bài 3 trang 58 SGK Toán 8 tập 1 - Cánh Diều

Cho một thanh kim loại đồng chất có khối lượng riêng 7,8 g/cm³.

a) Viết công thức tính khối lượng m (g) theo thể tích V (cm³). Hỏi m có phải là hàm số của V hay không? Vì sao?

b) Tính khối lượng của thanh kim loại đó khi biết thể tích của thanh kim loại đó là V = 1000 cm³.

Phương pháp:

Ta có: m = V.d (V: thể tích; d : khối lượng riêng).

Lời giải:

a) Công thức tính khối lượng m(g) theo thể tích V (cm³) là: m = 7,8 . V

Ta thấy với mỗi giá trị của V ta chỉ xác định được chỉ một giá trị tương ứng của m nên m là hàm số của V.

b) Khối lượng của thanh kim loại khi V = 1000 cm³ là: m = 7,8 . 1000 = 7 800 (g)

Bài 4 trang 58 SGK Toán 8 tập 1 - Cánh Diều

Dừa sáp là một trong những đặc sản lạ, quý hiếm và có giá trị dinh dưỡng cao, thường được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Viết công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp. Hỏi y có phải là hàm số của x hay không? Vì sao?

b) Hãy tính số tiền mà người mua phải trả khi mua 10 quả dừa sáp.

Phương pháp:

y = 200 000.x (công thức tính số tiền khi mua x quả dừa)

Lời giải:

Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp là

y = 200 000x (đồng) .

Vì với mỗi giá trị của x ta xác định được một giá trị y tương ứng nên y là hàm số của x.

b) Số tiền mà người mua phải trả khi mua 10 quả dừa sáp là:

200 000 . 10 = 2 000 000 (đồng).

Vậy số tiền mà người mua phải trả khi mua 10 quả dừa sáp là 2 000 000 đồng.

Bài 5 trang 59 SGK Toán 8 tập 1 - Cánh Diều

Bác Ninh gửi tiết kiệm 10 triệu đồng ở ngân hàng với kì hạn 12 tháng và không rút tiền trước kì hạn. Lãi suất ngân hàng quy định cho kì hạn 12 tháng là r%/năm.

a) Viết công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được sau khi hết kì hạn 12 tháng. Hỏi y có phải là hàm số của r hay không? Vì sao?

b) Tính số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng, biết r = 5,6.

Phương pháp:

Tiền lãi bằng số tiền gửi nhân với lãi suất

Lời giải:

a) Công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng là: y = 10r% (triệu đồng).

b) Với r = 5,6 thì số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng là:

y = 10r% = 10 . 5,6% = 0,56 (triệu đồng) = 560 000 (đồng).

Vậy với r = 5,6 thì số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng là 560 000 đồng.

Sachbaitap.com