Giải SGK Toán 8 trang 83 Kết nối tri thức tập 1

Bài 4.6 trang 83 SGK Toán 8 tập 1 - Kết nối tri thức

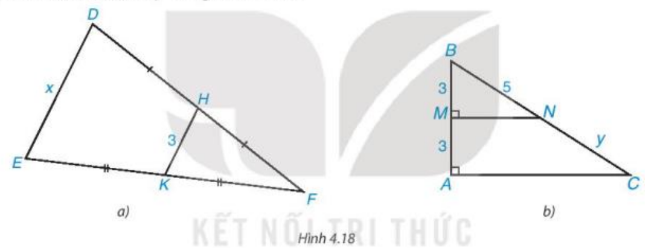
Tính các độ dài x, y trong Hình 4.18.

Lời giải:

• Hình 4.18a)

Ta có: DH = HF, H ∈ DF nên H là trung điểm của DF;

EK = KF, K ∈ EF nên K là trung điểm của EF.

Xét tam giác DEF có H, K lần lượt là trung điểm của DF, EF nên HK là đường trung bình của tam giác DEF.

Suy ra \(HK = \frac{1}{2}DE = \frac{1}{2}x\).

Do đó x = 2HK = 2 . 3 = 6.

• Hình 4.18b)

Vì MN ⊥ AB, AC ⊥ AB nên MN // AC.

Mà M là trung điểm của BC (vì AM = BM = 3)

Suy ra MN là đường trung bình của tam giác ABC.

Do đó y = NC = BN = 5.

Vậy x = 6; y = 5.

Bài 4.7 trang 83 SGK Toán 8 tập 1 - Kết nối tri thức

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.

a) Chứng minh tứ giác BMNC là hình thang.

b) Tứ giác MNPB là hình gì? Tại sao?

Lời giải:

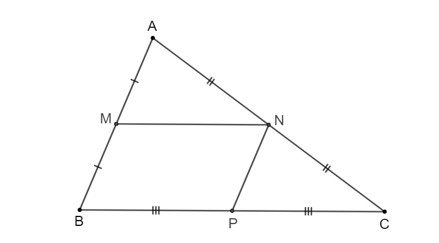
a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN // BC hay MN // BP.

Tứ giác BMNC có MN // BP nên tứ giác BMNC là hình thang (đpcm).

b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.

Tứ giác MNPB có MN // BP; BM // NP (chứng minh trên).

Do đó, tứ giác MNPB là hình bình hành.

Bài 4.8 trang 83 SGK Toán 8 tập 1 - Kết nối tri thức

Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.

a) Chứng minh DC // EM.

b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.

Lời giải:

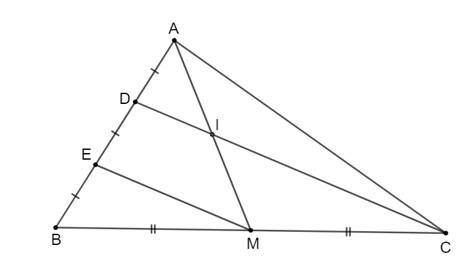
a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.

Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.

Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.

Do đó DC // EM (tính chất đường trung bình).

b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).

Mà DI // EM (vì DC // EM).

Do đó DI là đường trung bình của tam giác AEM.

Suy ra I là trung điểm của AM.

Bài 4.9 trang 83 SGK Toán 8 tập 1 - Kết nối tri thức

Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.

Lời giải:

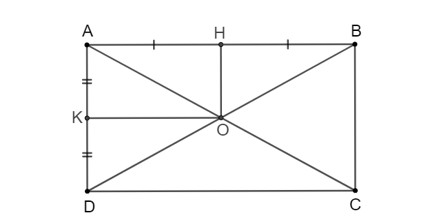
Vì ABCD là hình chữ nhật nên \(\widehat {BA{\rm{D}}} = {90^o}\) và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.

Suy ra AB ⊥ AD; O là trung điểm của AC và BD.

Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của tam giác ABD.

Suy ra OH // AD mà AB ⊥ AD nên OH ⊥ AB hay \(\widehat {AHO} = {90^o}\)

Tương tự, ta chứng minh được: OK ⊥ AD hay \(\widehat {AK{\rm{O}}} = {90^o}\).

Ta có: \(\widehat {BA{\rm{D}}} + \widehat {AHO} + \widehat {AK{\rm{O}}} + \widehat {HOK} = {360^o}\)

90°+90°+90°+\(\widehat {HOK}\)=360°

270°+\(\widehat {HOK}\)=360°

Suy ra \(\widehat {HOK}\)=360°−270°=90°

Tứ giác AHOK có \(\widehat {BA{\rm{D}}}\)=90°;ˆAHO=90°; \(\widehat {AHO}\)=90°;\(\widehat {AK{\rm{O}}}\)=90^o

Do đó, tứ giác AHOK là hình chữ nhật.

Sachbaitap.com