Giải Toán 7 trang 84 Chân trời sáng tạo tập 2

Bài 1 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC cân tại A (\(\widehat A < {90^o}\)). Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rẳng \(\Delta BFC = \Delta CEB\)

b) Chứng minh rằng \(\Delta AEH = \Delta AFH\)

c) Gọi I là trung điểm BC. Chứng minh rằng ba điểm A,H,I thẳng hàng.

Phương pháp:

a) Ta sử dụng định lí cạnh huyền – góc nhọn trong tam giác vuông

b) Từ câu a ta chứng minh 2 tam giác AHF = tam giác AHE nhờ những cạnh của 2 tam giác chứng minh được bằng nhau từ câu trên

c) Ta chứng minh AI và AH cùng là phân giác của góc A

Lời giải: 

a) Tam giác ABC cân tại A nên 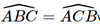 và AB = AC.

Xét $\Delta BEC$vuông tại E và $\Delta CFB$vuông tại F có:

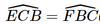(chứng minh trên).

BC chung.

Do đó (cạnh huyền - góc nhọn).

b) Do (cạnh huyền - góc nhọn) nên EC = FB (2 cạnh tương ứng).

Mà AB = AC nên AB - FB = AC - EC hay AF = AE.

Xét vuông tại F và $\Delta AHE$vuông tại E có:

AF = AE (chứng minh trên).

AH chung.

Do đó (cạnh huyền - cạnh góc vuông). 

c) DABC có hai đường cao BE, CF cắt nhau tại H nên H là trực tâm của $△$ABC.

Suy ra AH  BC (1).

Xét AIB và AIC có:

AB = AC (chứng minh trên).

IB = IC (do I là trung điểm của BC).

AI chung.

Suy ra AIB = AIC (c.c.c).

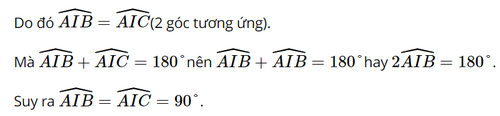
Do đó AI BC (2).

Từ (1) và (2) suy ra A, H, I thẳng hàng.

Bài 2 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh rằng tam giác ABM cân.

b) Chứng minh rằng \(\Delta ABC = \Delta MBC\)

Phương pháp:

a) Ta chứng minh BM = BA thông qua việc chứng minh 2 tam giác BHA và BHM bằng nhau

b) Ta chứng minh góc ABH = góc MBH sau đó chứng minh 2 tam giác đề bài yêu cầu bằng nhau theo trường hợp c-g-c

Lời giải: 

a) Xét vuông tại H và $\Delta MHB$vuông tại H có:

AH = MH (theo giả thiết).

BH chung.

Do đó (2 cạnh góc vuông).

Suy ra AB = MB (2 cạnh tương ứng).

Tam giác ABM có AB = MB nên tam giác ABM cân tại B. 

b) Do (2 cạnh góc vuông) nên 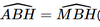(2 góc tương ứng).

Xét và $\Delta MBC$có:

AB = MB (chứng minh trên).

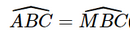(chứng minh trên).

BC chung.

Do đó (c - g - c).

Bài 3 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.

a) Chứng minh rằng AD = AC.

b) Chứng minh rằng \(\widehat {ADH} = \widehat {BAH}\)

Phương pháp:

a) Ta chứng minh tam giác ACD cân tại A sau đó suy ra AC = AD

b) Ta chứng minh \(\widehat {BAH} + \widehat {HAC} = {90^o} = \widehat {HAC} + \widehat {HCA}\) và \(\widehat D = \widehat C\)

Lời giải: 

a) Trên tia đối của HC lấy D sao cho HC = HD nên H là trung điểm của CD.

AH CD tại trung điểm H của CD nên AH là đường trung trực của CD.

Do đó AC = AD.

b) Tam giác ACD có AC = AD nên tam giác ACD cân tại A.

Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ \(BE \bot AN\)(E ∈ AN).

a) Chứng minh rằng BE là tia phân giác của giác ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của BH với CE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân. 

Phương pháp:

a) Ta chứng minh \(\widehat {ABE} = \widehat {NBE}\) bằng cách chứng minh 2 tam giác BAF và BNF bằng nhau .

b) Ta chứng minh NK song song với CA do có 2 góc so le trong bằng nhau

c) Ta chứng minh góc BGC bằng góc BCG

Lời giải: 

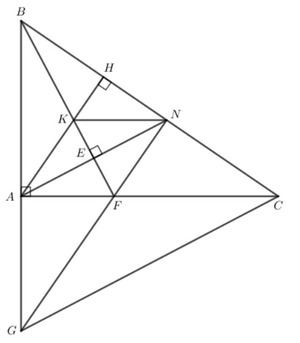
a) XétBEA vuông tại E và BEN vuông tại E có:

BA = BN (theo giả thiết).

BE chung.

Suy ra BEA = BEN (cạnh huyền - cạnh góc vuông).

b) Tam giác BAN có hai đường cao AH và BE cắt nhau tại K nên K là trực tâm của tam giác BAN.

Do đó NK AB.

Mà AC AB nên NK // AC.

Do đó (góc nhọn - cạnh góc vuông).

Suy ra AG = NC (2 cạnh tương ứng).

Mà BA = BN nên BA + AG = BN + NC hay BG = BC.

Tam giác BGC có BG = BC nên tam giác BGC cân tại B.

Bài 5 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác nhọn ABC (AB < AC), vẽ đường cao AH. Đường trung trực của BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng \(\widehat {BMN} = \widehat {HAC}\)

b) Kẻ \(MI \bot AH\)(I ∈ AH), gọi K là giao điểm của AH và BM. Chứng minh rằng I là trung điểm của AK.

Phương pháp:

a) Ta xét tam giác BMC cân tại M nên \(\widehat {MBC} = \widehat {MCB}\)

Nên \(\widehat {BMN} = \widehat {HAC} = {90^o} - \widehat {MBC} = {90^o} - \widehat {MBC}\)

b) Ta chứng minh I là trung điểm của AK do \(\Delta MAI = \Delta MKI\)(g-c-g) 

Lời giải: 

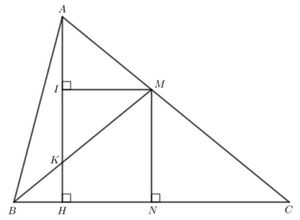
a) Do M nằm trên đường trung trực của BC nên MB = MC.

Xét $\Delta BMN$vuông tại N và $\Delta CMN$vuông tại N có:

MB = MC (chứng minh trên).

MN chung.

Do đó (cạnh huyền - cạnh góc vuông).

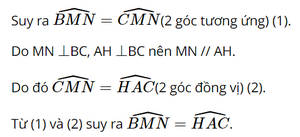
MI chung.

Do đó ΔAMI=ΔKMI(góc nhọn - cạnh góc vuông).

Suy ra AI = KI (2 cạnh tương ứng).

Mà I nằm giữa A và K nên I là trung điểm của AK.

Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.

a) Chứng minh rằng \(\Delta \)MFN = \(\Delta \)PFD

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của GK. Chứng minh rằng ba điểm M, H, K thẳng hàng.

Phương pháp:

a) Chứng minh \(\Delta \)MFN = \(\Delta \)PFD theo trường họp cạnh góc cạnh

Sử dụng tính chất của điểm đối xứng qua một điểm, trung điểm của 1 đoạn thẳng và 2 góc đối đỉnh

b) Chứng minh H là trọng tâm của tam giác MPD sau đó dựa vào tính chất ta suy ra M, H, K thẳng hàng

Lời giải: 

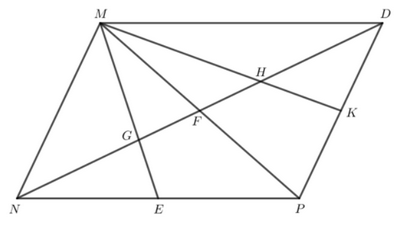
a) Tam giác MNP có đường trung tuyến NF nên F là trung điểm của MP.

Do đó FM = FP.

Xét $\Delta MFN$và $\Delta PF\text{D}$có:

MF = PF (chứng minh trên).

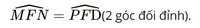
FN = FD (theo giả thiết).

Do đó $\Delta MFN=\Delta PF\text{D}$(c.g.c).

b) Tam giác MNP có G là giao điểm hai đường trung tuyến ME và NF nên G là trọng tâm của tam giác MNP.

Do đó NG = NF.

Suy ra GF = NF.

Do F là trung điểm của GH nên GF = HF.

Suy ra HF = 1/3 NF.

Mà NF = DF nên HF = DF.

Suy ra DH =  DF.

Tam giác MDP có đường trung tuyến DF và DH = DF nên H là trọng tâm của tam giác MDP.

Lại có MK là đường trung tuyến của tam giác MDP nên M, H, K thẳng hàng.

Bài 7 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A có AB = \(\dfrac{1}{2}\)AC, AD là tia phân giác \(\widehat {BAC}\)(D ∈ BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH\( \bot \)KC. 

Phương pháp:

a) Chứng minh BD = DE thông qua việc chứng minh 2 tam giác BAD và EAD bằng nhau

b) Chứng minh \(\Delta \)CDK cân tại D do có 2 cạnh bên DK = DC

c) Chứng minh \(\Delta \)KAC vuông cân tại A và AD là phân giác nên cũng là đường cao của \(\Delta \)KAC \( \Rightarrow \)AH\( \bot \)KC

Lời giải: 

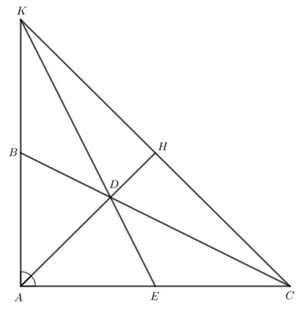
a) Do E là trung điểm của AC nên AE = AC.

Mà AB = AC nên AE = AB.

AD chung.

Do đó (c.g.c).

Suy ra DB = DE (2 cạnh tương ứng).

Do đó g.c.g).

Suy ra DK = DC (2 cạnh tương ứng) và AK = AC (2 cạnh tương ứng).

Tam giác DCK có DK = DC nên tam giác DCK cân tại D.

Do AK = AC, mà AC = 2AB nên AK = 2AB.

Mà A, B, K thẳng hàng nên B là trung điểm của AK.

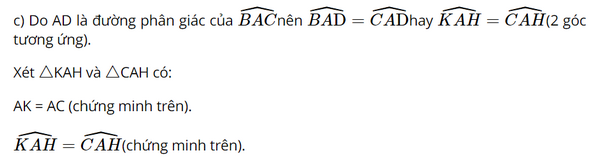
AH chung.

Suy ra KAH = CAH (c.g.c).

Bài 8 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Ở Hình 1, cho biết AE = AF và \(\widehat {ABC} = \widehat {ACB}\). Chứng minh AH là đường trung trực của BC.

Phương pháp:

Ta chứng minh A và H cùng thuộc đường trung trực của đoạn BC thông qua chứng minh chúng cách đều 2 đầu mút của đoạn BC.

Lời giải: 

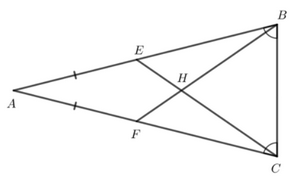
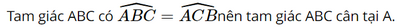
Do đó AB = AC.

Suy ra A nằm trên đường trung trực của BC (1).

Mà AE = AF nên AB - AE = AC - AF hay BE = CF.

Xét và có:

BE = CF (chứng minh trên).

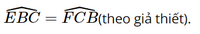
BC chung.

Do đó (c.g.c).

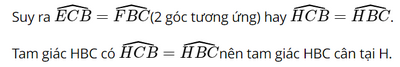
Do đó HB = HC.

Suy ra H nằm trên đường trung trực của BC (2).

Từ (1) và (2) suy ra AH là đường trung trực của BC.

Bài 9 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng \(\widehat {EBH} = \widehat {ACM}\)

c) Chứng minh rằng \(EB \bot BC\)

Phương pháp:

a)Ta chứng minh \(\Delta \)BME có 2 cạnh bên hoặc 2 góc đáy bằng nhau thông qua việc chứng minh 2 tam giác EHB và MHB bằng nhau.

b)Ta chứng minh \(\widehat {EBH} = \widehat {ACM}\)do cùng = \(\widehat {MBH}\)

c)Ta chứng minh\(\widehat {EBH} + \widehat {BCE} = {90^o}\)

Lời giải: 

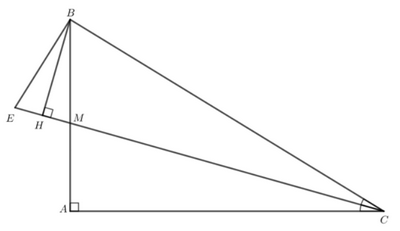
a) Trên tia đối của tia HC lấy điểm E sao cho HE = HM nên H là trung điểm của ME.

Ta thấy BH vuông góc với ME tại trung điểm H của ME nên BH là đường trung trực của ME.

Do đó BM = BE.

Tam giác MBE có BM = BE nên tam giác MBE cân tại B.

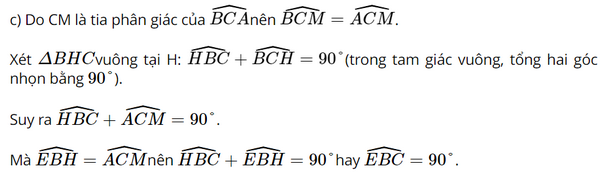
Do đó EB BC.

Bài 10 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

Phương pháp:

Ta chứng minh N là trực tâm của tam giác MIK

Lời giải: 

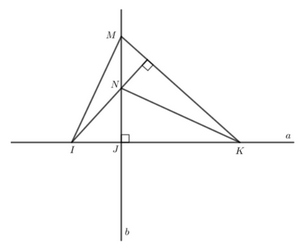
Xét tam giác MIK có MJ IK, IN MK.

Mà MJ cắt IN tại N nên N là trực tâm của tam giác MIK.

Do đó NK vuông góc với MI.

Sachbaitap.com