Bài 1, 2, 3, 4 trang 58 SGK Toán lớp 5 - Luyện tập
Bài 1, 2, 3, 4 trang 58 sách giáo khoa (SGK) Toán lớp 5 bài Luyện tập. Bài 3 Một người đi xe đạp, trong 3 giờ đầu mỗi giờ đi được 10,8 km, trong 4 giờ tiếp theo mỗi giờ đi được 9,52km. Hỏi người đó đi được bao nhiêu ki-lô-mét?
- Bài 1, 2, 3 trang 59 SGK Toán lớp 5 - Nhân một số thập phân với một số thập phân
- Bài 1, 2, 3 trang 60 SGK Toán lớp 5 - Luyện tập
- Bài 1, 2, 3 trang 61 SGK Toán lớp 5 - Luyện tập
- Bài 1, 2, 3, 4 trang 61, 62 SGK Toán lớp 5 - Luyện tập chung
Xem thêm: CHƯƠNG II: SỐ THẬP PHÂN. CÁC PHÉP TÍNH VỚI SỐ THẬP PHÂN
Bài 1 trang 58 SGK Toán lớp 5
Câu hỏi:
a) Tính nhẩm:
\(1,48 \times 10\) \(5,12 \times 100\) \(2,571 \times 1000\)
\(15,5 \times 10\) \(0,9 \times 100\) \(0,1 \times 1000\)
b) Số \(8,05\) phải nhân với số nào để được tích là \(80,5\,; \;805\,;\; 8050\,;\; 80500\) ?
Phương pháp:
Muốn nhân một số thập phân với \(10,\;100,\;1000,\;...\) ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số.
Lời giải:
a) \(1,48 \times 10= 14,8\) \(5,12 \times 100= 512\)
\(2,571 \times 1000=2571\) \(15,5 \times 10=155\)
\(0,9 \times 100=90\) \(0,1 \times 1000=100\)
b) \(8,05 \times 10 = 80,5\); \(8,05 \times 100 = 805\)
\( 8,05 \times 1000 = 8050\); \( 8,05 \times 10 000 = 80 500\).
Bài 2 trang 58 SGK Toán lớp 5
Câu hỏi:
Đặt tính rồi tính:
a) 7,69 x 50; b) 12,6 x 800; c) 12,82 x 40; d) 82,14 x 600
Phương pháp:
Để nhân một số thập phân với một số tự nhiên ta làm như sau:
- Nhân như nhân các số tự nhiên.
- Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Lời giải:
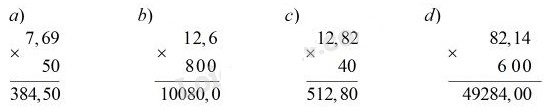
Bài 3 trang 58 SGK Toán lớp 5
Câu hỏi:
Một người đi xe đạp, trong 3 giờ đầu mỗi giờ đi được 10,8 km, trong 4 giờ tiếp theo mỗi giờ đi được 9,52km. Hỏi người đó đi được bao nhiêu ki-lô-mét?
Phương pháp:
- Tính quãng đường người đó đi được trong \(3\) giờ đầu \(=\) số km đi được trong mỗi giờ đầu \(\times 3\).
- Tính quãng đường người đó đi được trong \(4\) giờ sau \(=\) số km đi được trong mỗi giờ sau \(\times 4\).
- Quãng đường người đó đã đi \(=\) quãng đường đi được trong \(3\) giờ đầu \(+\) quãng đường đi được trong \(4\) giờ sau.
Lời giải:
Trong 3 giờ đầu người đó đi được:
10,8 x 3 = 32,4 (km)
Trong 4 giờ tiếp người đó đi được:
9,52 x 4 = 38,08 (km)
Người đó đã đi được tất cả:
32,4 + 38,08 = 70,48 (km)
Đáp số: 70,48 (km).
Bài 4 trang 58 SGK Toán lớp 5
Câu hỏi:
Tìm số tự nhiên \(x\), biết: \(2,5 \times x < 7\).
Phương pháp:
Thay \(x=0;\; x=1;\;x=2;\;x=3;\;...\) vào biểu thức \(2,5 \times x\), sau đó so sánh kết quả với \(7\).
Lời giải:
Nếu x = 0 thì 2,5 x 0 = 0 < 7
Nếu x = 1 thì 2,5 x 1 = 2,5 < 7
Nếu x = 2 thì 2,5 x 2 = 5 < 7
Nếu x = 3 thì 2,5 x 3 = 7,5 > 7 (loại)
Vậy x là các số: 0; 1; 2.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 1, 2, 3 trang 179, 180 SGK Toán lớp 5 - Luyện tập chung (01/06)
- Bài 1, 2 trang 179 SGK Toán lớp 5 - Luyện tập chung (01/06)
- Bài 1, 2, 3 trang 178 SGK Toán lớp 5 - Luyện tập chung (01/06)
- Bài 1, 2, 3, 4, 5 trang 177, 178 SGK Toán lớp 5 - Luyện tập chung (01/06)
- Bài 1, 2, 3, 4, 5 trang 176, 177 SGK Toán lớp 5 - Luyện tập chung (01/06)
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
