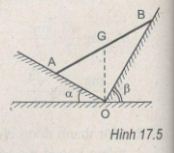
Một thanh AB đồng chất, khối lượng m = 2,0 kg tựa lên hai mặt phẳng nghiêng không ma sát, với các góc nghiêng α = 30° và β = 60°. Biết giá của trọng lực của thanh đi qua giao tuyến O của hai mặt phẳng nghiêng (H.17.5). Lấy g = 10 m/s2. Xác định áp lực của thanh lên mỗi mặt phẳng nghiêng.

Xem thêm: Bài 17: Cân Bằng Của Vật Rắn Chịu Tác Dụng Của Hai Lực Và Của Ba Lực Không Song Song

Một thanh AB đồng chất, khối lượng m = 2,0 kg tựa lên hai mặt phẳng nghiêng không ma sát, với các góc nghiêng α = 30° và β = 60°. Biết giá của trọng lực của thanh đi qua giao tuyến O của hai mặt phẳng nghiêng (H.17.5). Lấy g = 10 m/s². Xác định áp lực của thanh lên mỗi mặt phẳng nghiêng.

Hướng dẫn trả lời:

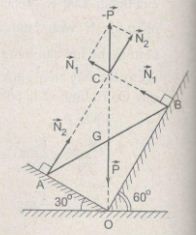
Thanh AB chịu ba lực cân bàng là \(\overrightarrow P ,\overrightarrow {{N_1}} \) và \(\overrightarrow {{N_2}} \) . Vì mặt phẳng nghiêng không ma sát nên hai phản lực \(\overrightarrow {{N_1}} \) và \(\overrightarrow {{N_2}} \)vuông góc với các mặt phẳng nghiêng. Ta trượt các vectơ lực trên giá của chúng đến điểm đồng quy C (H.17.5G).

Từ tam giác lực, ta được :

N₁ = Psin30° = 20.0,5 = 10 N

N₂= Pcos30° = 20.\({{\sqrt 3 } \over 2}\) = 17,3 ≈ 17 N

Theo định luật III Niu-tơn thì áp lực của thanh lên mặt phẳng nghiêng có độ lớn bằng phản lực của mặt phẳng nghiêng lên thanh.

Sachbaitap.com

Bài tiếp theo

Xem lời giải SGK - Vật lí 10 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.