Bài 21, 22, 23, 24, 25, 26, 27 trang 46, 47, 48 SGK Toán 8 tập 1 - Phép cộng các phân thức đại số - luyện tập

Bài 21 trang 46 SGK Toán lớp 8 tập 1

Câu hỏi:

Thực hiện các phép tính sau

a.\( \dfrac{3x-5}{7}+\dfrac{4x+5}{7}\);

b.\( \dfrac{5xy-4y}{2x^{2}y^{3}}+\dfrac{3xy+4y}{2x^{2}y^{3}}\)

c.\( \dfrac{x+1}{x-5}+\dfrac{x-18}{x-5}+\dfrac{x+2}{x-5}\).

Phương pháp:

Áp dụng quy tắc cộng hai phân thức cùng mẫu: Muốn cộng hai phân thức cùng mẫu thức ta cộng các tử thức với nhau, giữ nguyên mẫu thức.

                     \( \dfrac{A}{B}+\dfrac{C}{B}=\dfrac{A+C}{B}\)

Lời giải:

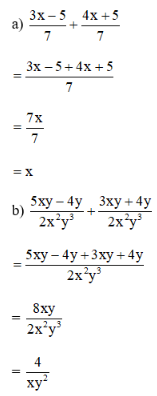
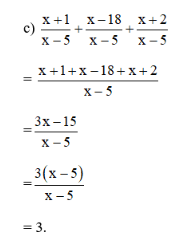
Bài 22 trang 46 SGK Toán lớp 8 tập 1

Câu hỏi:

Áp dụng quy tắc đổi dấu để các phân thức có cùng mẫu thức rồi làm tính cộng phân thức:

a. \( \dfrac{2x^{2}-x}{x-1}+\dfrac{x+1}{1-x}+\dfrac{2-x^{2}}{x-1}\);

b. \( \dfrac{4-x^{2}}{x-3}+\dfrac{2x-2x^{2}}{3-x}+\dfrac{5-4x}{x-3}\).

Phương pháp:

Áp dụng quy tắc đổi dấu, quy tắc cộng hai phân thức cùng mẫu.

\(A=-(-A)\)

\(\dfrac{A}{B} = \dfrac{{ - A}}{{ - B}}\)

\( \dfrac{A}{B}+\dfrac{C}{B}=\dfrac{A+C}{B}\)

Lời giải:

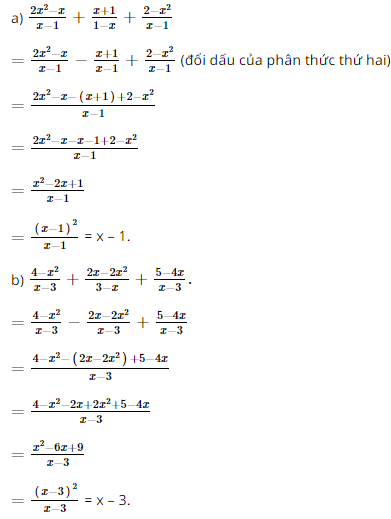
Bài 23 trang 46 SGK Toán lớp 8 tập 1

Câu hỏi:

Làm các phép tính sau:

\( \dfrac{y}{2x^{2}-xy}+\dfrac{4x}{y^{2}-2xy}\);

\( \dfrac{1}{x+2}+\dfrac{3}{x^{2}-4}+\dfrac{x-14}{(x^{2}+4x+4)(x-2)}\);

\( \dfrac{1}{x+2}+\dfrac{1}{(x+2)(4x+7)}\);

\( \dfrac{1}{x+3}+\dfrac{1}{(x+3)(x+2)}+\dfrac{1}{(x+2)(4x+7)}\)

Phương pháp:

Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.

\( \dfrac{A}{B}+\dfrac{C}{D}=\dfrac{AD}{BD}+\dfrac{CB}{DB}=\dfrac{AD+BC}{BD}\)

\(\dfrac{A}{B} = \dfrac{{ - A}}{{ - B}}\)

Lời giải:

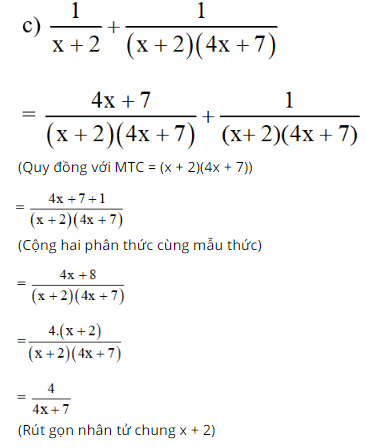
Bài 24 trang 46 SGK Toán lớp 8 tập 1

Câu hỏi:

Một con mèo đuổi bắt một con chuột. Lần đầu mèo chạy với vận tốc \(x\) m/s. Chạy được \(3\,m\) thì mèo bắt được chuột. Mèo vờn chuột \(40\) giây rồi thả cho chuột chạy. Sau đó \(15\) giây mèo lại đuổi bắt, nhưng với vận tốc nhỏ hơn vận tốc lần đầu là \(0,5\) m/s. Chạy được \(5\,m\) mèo lại bắt được chuột. Lần này thì mèo cắn chết chuột. Cuộc săn đuổi kết thúc.

Hãy biểu diễn qua \(x\):

- Thời gian lần thứ nhất mèo bắt được chuột

Lời giải:

- Vì vận tốc lần đầu mèo chạy là \(x\) (m/s) nên vận tốc lần thứ hai mèo chạy là \(x - 0,5\) (m/s)

- Vì quãng đường để mèo bắt được chuột lần thứ nhất là 3m nên thời gian lần thứ nhất mèo bắt được chuột là \( \dfrac{3}{x}\) (giây)

- Vì quãng đường để mèo bắt được chuột lần thứ hai là 5m nên thời gian lần thứ hai mèo bắt được chuột là  \( \dfrac{5}{x-0,5}\) (giây)

- Thời gian kể từ lúc đầu đến khi kết thúc cuộc săn là: \( \dfrac{3}{x} + 40 + 15 +  \dfrac{5}{x-0,5}\) (giây)

hay  \( \dfrac{3}{x} + 55+  \dfrac{5}{x-0,5}\) (giây)

Bài 25 trang 47 SGK Toán lớp 8 tập 1

Câu hỏi:

Làm tính cộng các phân thức sau:

\(\dfrac{5}{{2{x^2}y}} + \dfrac{3}{{5x{y^2}}} + \dfrac{x}{{{y^3}}}\)

\(\dfrac{{x + 1}}{{2x + 6}} + \dfrac{{2x + 3}}{{x\left( {x + 3} \right)}}\)

\(\dfrac{{3x + 5}}{{{x^2} - 5x}} + \dfrac{{25 - x}}{{25 - 5x}}\)

\({x^2} + \dfrac{{{x^4} + 1}}{{1 - {x^2}}} + 1\)

\(\dfrac{{4{x^2} - 3x + 17}}{{{x^3} - 1}} + \dfrac{{2x - 1}}{{{x^2} + x + 1}} + \dfrac{6}{{1 - x}}\)

Phương pháp:

Áp dụng:

- Quy tắc đổi dấu

\(\dfrac{A}{B} = \dfrac{{ - A}}{{ - B}}\)

- Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.

\( \dfrac{A}{B}+\dfrac{C}{D}=\dfrac{AD}{BD}+\dfrac{CB}{DB}=\dfrac{AD+BC}{BD}\)

Lời giải:

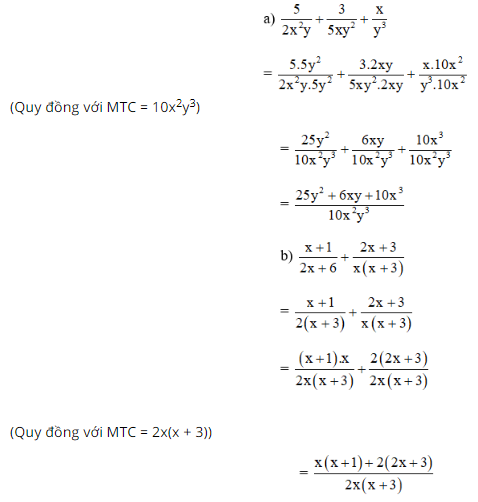
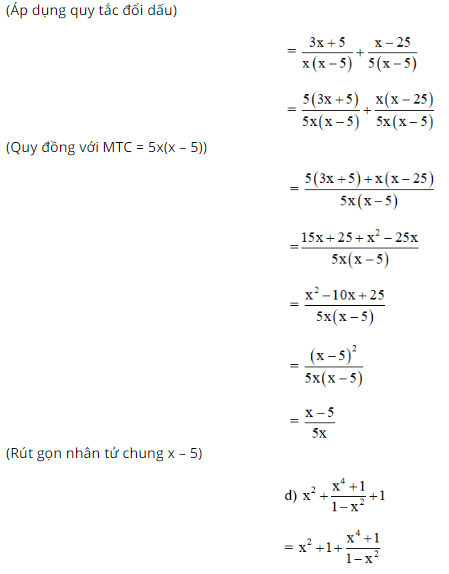
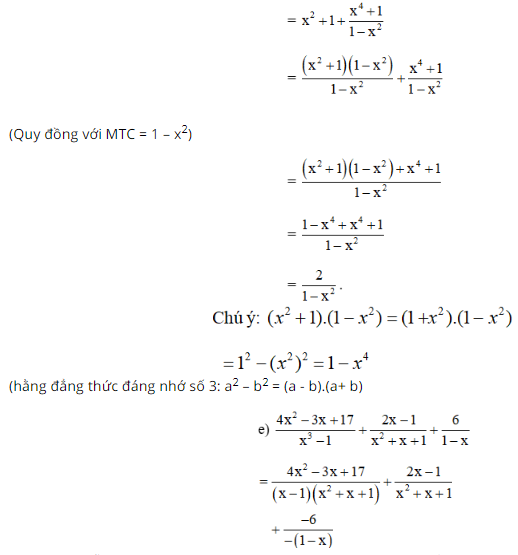
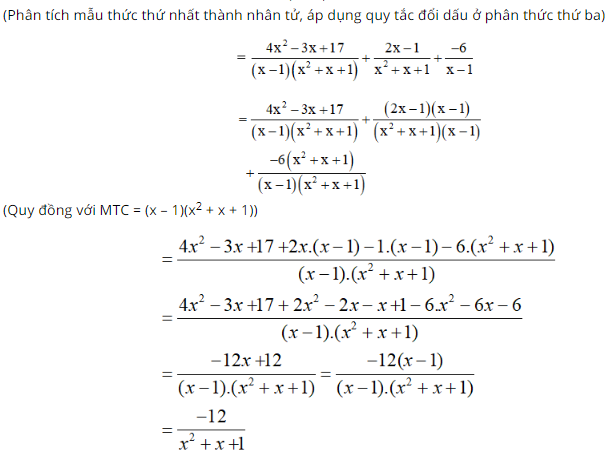
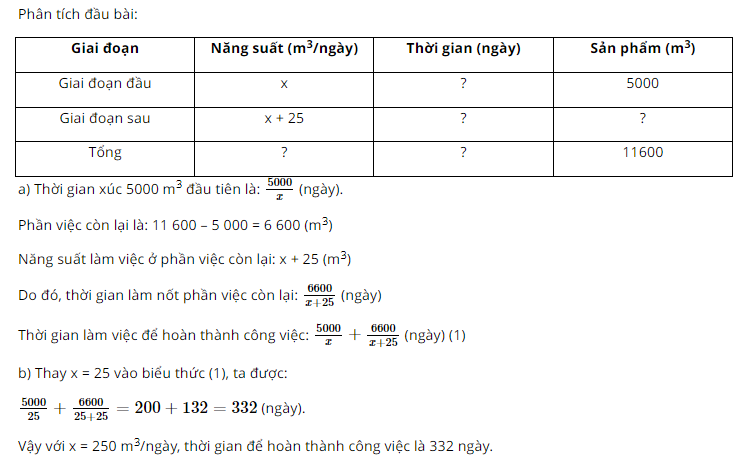
Bài 26 trang 47 SGK Toán lớp 8 tập 1

Câu hỏi:

Một đội máy xúc trên công trường đường Hồ Chí Minh nhận nhiệm vụ xúc \(11600{m^3}\) đất. Giai đoạn đầu còn nhiều khó khăn nên máy làm việc với năng suất trung bình \(x\left( {{m^3}} \right)\)/ngày và đội đào được \(5000{m^3}\). Sau đó công việc ổn định hơn, năng suất của máy tăng \(25{m^3}\)/ngày.

a) Hãy biểu diễn:

- Thời gian xúc \(5000{m^3}\) đầu tiên;

- Thời gian làm nốt phần việc còn lại;

- Thời gian làm việc để hoành thành công việc.

b) Thời gian làm việc để hoàn thành công việc với \(x = 250{m^3}\)/ ngày.

Phương pháp:

Áp dụng:

- Công thức: công việc \(=\) năng suất \( \times \) thời gian.

- Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.

Lời giải:

Bài 27 trang 48 SGK Toán lớp 8 tập 1

Câu hỏi:

Đố: Rút gọn rồi tính giá trị của biểu thức: \(\dfrac{{{x^2}}}{{5{\rm{x}} + 25}} + \dfrac{{2\left( {x - 5} \right)}}{x} + \dfrac{{50 + 5{\rm{x}}}}{{x\left( {x + 5} \right)}}\) tại \(x = -4\).

Nếu coi tử số của phân số tối giản mà em tìm được là ngày còn mẫu số là tháng thì đó chính là một ngày lễ trên thế giới. Đố em biết đó là ngày gì?

Phương pháp:

Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.

               \( \dfrac{A}{B}+\dfrac{C}{D}=\dfrac{AD}{BD}+\dfrac{CB}{DB}=\dfrac{AD+BC}{BD}\)

- Sau đó, thay giá trị tương ứng của \(x\) vào phân thức đã rút gọn.

Lời giải:

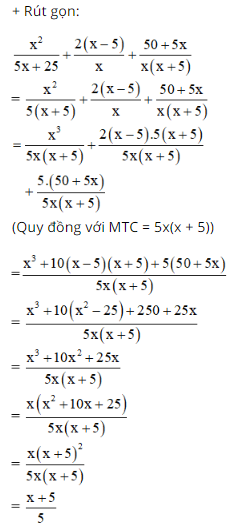
Sachbaitap.com