Bài 3.15 trang 11 Sách bài tập (SBT) Vật Lí 12
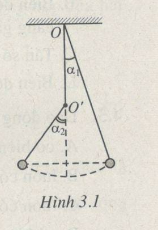
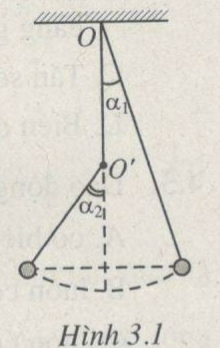
Một con lắc đơn dài 1,0 m. Phía dưới điểm treo O trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm O' cách O một đoạn OO' = 0,5 m, sao cho con lắc vấp vào đinh khi dao động (H.3.1).
3.15. Một con lắc đơn dài 1,0 m. Phía dưới điểm treo O trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm O' cách O một đoạn OO' = 0,5 m, sao cho con lắc vấp vào đinh khi dao động (H.3.1). Kéo con lắc lệch khỏi phương thẳng đứng một góc \(\alpha\)1 =10° rồi thả không vận tốc đầu. Bỏ qua ma sát. Hãy tính :
a) Biên độ góc của con lắc ở hai bên vị trí cân bằng.
b) Chu kì dao động của con lắc. Lấy g = 9,8 m/s2. Hình 3.1
Hướng dẫn giải chi tiết
a) Biên độ góc của con lắc ở hai bên vị trí cân bằng.
Theo định luật bảo toàn năng lượng ta suy ra hai vị trí biên phải ở cùng 1 độ cao (H3.1.G)
\(\eqalign{
& {h_A} = {h_B}l \cr
& (1 - \cos {\alpha _1}) = {l \over 2}(1 - \cos {\alpha _2}) \cr
& \Rightarrow \cos {\alpha _2} = 2\cos {\alpha _1} - 1 \cr
& = 2\cos {10^0} - 1 = 0,9696 \cr
& \Rightarrow {\alpha _0} = {14^0} \cr}\)
b) Chu kì dao động của con lắc
\(\eqalign{
& T = {{{T_1} - {T_2}} \over 2};\,\,{T_1} = 2\pi \sqrt {{l \over g}} {\mkern 1mu} ;\,\,{T_2} = 2\pi \sqrt {{l \over {2g}}} \cr
& T = 2\pi \sqrt {{l \over g}} \left( {1 + {1 \over {\sqrt 2 }}} \right) \cr
& = 3,14\sqrt {{1 \over {9,8}}} \left( {1 + {1 \over {\sqrt 2 }}} \right) = 1,7s \cr} \)
Sachbaitap.com
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 41 : Cấu tạo vũ trụ
- Bài 40 : Các hạt sơ cấp
- CHƯƠNG VII: TỪ VI MÔ ĐÉN VĨ MÔ
- Bài tập cuối chương VII - Hạt nhân nguyên tử
- Bài 39 : Phản ứng nhiệt hạch
- Bài 38. Phản ứng phân hạch
- Bài 37. Phóng xạ
- Bài 36. Năng lượng liên kết của hạt nhân. Phản ứng hạt nhân
- Bài 35. Tính chất và cấu tạo hạt nhân
- CHƯƠNG VII. HẠT NHÂN NGUYÊN TỬ
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!