Bài 34, 35, 36 trang 25, 26 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình
Bài 34, 35 trang 25; bài 36 trang 26 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình. Bài 36 (Bài toán nói về cuộc đời nhà toán học Đi-ô-phăng, lấy trong Hợp tuyển Hy Lạp - Cuốn sách gồm 46 bài toán về số, viết dưới dạng thơ trào phúng).
- Bài 37, 38, 39 trang 30 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình...
- Bài 40, 41, 42, 43, 44, 45, 46, 47, 48, 49 trang 31, 32 SGK Toán 8 tập 2 - Luyện tập
- Bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34 SGK Toán 8 tập 2 - Ôn tập chương 3
- Bài 1, 2, 3, 4 trang 37 SGK Toán 8 tập 2 - Liên hệ giữa thứ tự và phép cộng
Xem thêm: Chương III. Phương trình bậc nhất một ẩn
Bài 34 trang 25 SGK Toán lớp 8 tập 2
Câu hỏi:
Mẫu số của một phân số lớn hơn tử số của nó là 3 đơn vị. Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới bằng \(\dfrac{1}{2}\) . Tìm phân số ban đầu.
Phương pháp:
B1: Đặt tử số là ẩn tìm điều kiện của ẩn và biểu diễn phân số đó theo ẩn.
B2: Dựa vào dữ kiện của đề bài lập phương trình.
B3: Giải phương trình.
B4: Kết luận (Kiểm tra nghiệm tìm được có thỏa mãn các điều kiện của ẩn không)
|
|
Tử số |
Mẫu số |
Phân số |
|
Ban đầu |
x |
x+3 |
\(\frac{x}{{x + 3}}\) |
|
Sau khi tăng |
x+2 |
(x+3)+2 = x+5 |
\(\frac{{x + 2}}{{x + 5}}\) |
Lời giải:
Gọi x là tử số của phân số (x ∈ ℤ; x ≠ -3)
Vì mẫu hơn tử số 3 đơn vị nên mẫu số là: x + 3.
Phân số ban đầu là ![]()
Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới là: 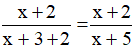 .
.
Theo giả thiết ta có: 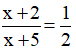 .
.
Suy ra: 2(x + 2) = 1.(x + 5)
2x + 4 = x + 5
x = 1 (thỏa mãn điều kiện)
Do đó tử số của phân số là 1.
Mẫu số của phân số là 1 + 3 = 4.
Vậy phân số ban đầu là ![]() .
.
Bài 35 trang 25 SGK Toán lớp 8 tập 2
Câu hỏi:
Học kì một, số học sinh giỏi của lớp 8A bằng 1/8 số học sinh cả lớp. Sang học kì hai, có thêm 3 bạn phấn đấu trở thành học sinh giỏi nữa, do đó số học sinh giỏi bằng 20% số học sinh cả lớp. Hỏi lớp 8A có bao nhiêu học sinh?
Phương pháp:
B1: Đặt số học sinh của cả lớp là ẩn, biểu diễn học sinh giỏi của mỗi kỳ theo ẩn đó.
B2: Lập trình biểu diễn kết nối giữa các đại lượng
B3: Set up the method.
B4: Kết luận (Kiểm tra tìm kiếm được thỏa mãn các điều kiện của ẩn)
Lời giải:
Gọi số học sinh của lớp 8A là x (x ∈ N*; x > 3).
Số học sinh giỏi của học kì I là : ![]()
Sang học kì 2, số học sinh giỏi bằng 20% số học sinh cả lớp nên số học sinh giỏi của học kì II là : 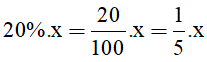
Vì số học sinh giỏi của học kì II nhiều hơn số HSG của học kì I 3 học sinh nên ta có :
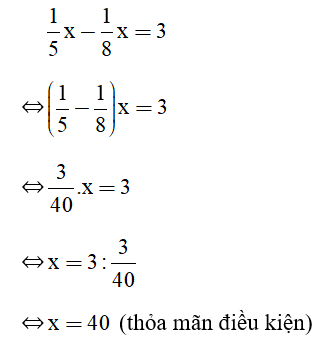
Vậy lớp 8A có 40 học sinh.
Bài 36 trang 26 SGK Toán lớp 8 tập 2
Câu hỏi:
(Bài toán nói về cuộc đời nhà toán học Đi-ô-phăng, lấy trong Hợp tuyển Hy Lạp - Cuốn sách gồm 46 bài toán về số, viết dưới dạng thơ trào phúng).

Phương pháp:
B1: Đặt số tuổi của ông Đi – ô – phăng là ẩn, đặt điều kiện cho ẩn
B2: Biểu diễn các đại lượng còn lại theo ẩn.
B3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.
B4: Kết luận (Kiểm tra nghiệm tìm được có thỏa mãn các điều kiện của ẩn không)
Lời giải:
Gọi x là số tuổi của ông Đi-ô-phăng (x > 0, x ∈ N).
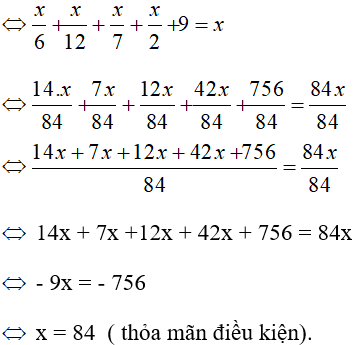
Vậy nhà toán học Đi-ô-phăng thọ 84 tuổi.
sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 41, 42, 43, 44, 45, 46, 47 trang 132, 133 SGK Toán 8 tập 1 - Ôn tập chương 2 (28/06)
- Bài 37, 38, 39, 40 trang 130, 131 SGK Toán 8 tập 1 - Diện tích đa giác (28/06)
- Bài 32, 33, 34, 35, 36 trang 128, 129 SGK Toán 8 tập 1 - Diện tích hình thoi (28/06)
- Bài 26, 27, 28, 29, 30, 31 trang 125, 126 SGK Toán 8 tập 1 - Diện tích hình thang (28/06)
- Bài 19, 20, 21, 22, 23, 24, 25 trang 121 SGK Toán 8 tập 1 - Luyện tập (28/06)
- Ôn tập cuối năm
- Chương IV. Hình lăng trụ đứng. Hình chóp đều
- Chương III. Tam giác đồng dạng
- Chương IV. Bất phương trình bậc nhất một ẩn
- Chương III. Phương trình bậc nhất một ẩn
- GIẢI SGK TOÁN 8 TẬP 2
- Chương II: Đa giác. Diện tích đa giác
- Chương I. Tứ giác
- Chương II. Phân thức đại số
- Chương I. Phép nhân và phép chia các đa thức
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
