Bài 56, 57, 58, 59, 60, 61 trang 92 SGK Toán 8 tập 2 - Ôn tập chương 3

Bài 56 trang 92 SGK Toán lớp 8 tập 2

Câu hỏi:

Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau

a) AB = 5cm, CD = 15cm;

b) AB = 45dm; CD = 150cm;

c) AB = 5CD.

Lời giải:

a. \(AB  = 5cm\) và \(CD = 15cm\)

\( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{5}{{15}} = \dfrac{1}{3}\)

b.  \(AB = 45dm = 450cm\) và \(CD = 150 cm\)

\( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{450}}{{150}} = 3\)

c. \(AB = 5CD\) \( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{5CD}}{{CD}} = 5\)

Bài 57 trang 92 SGK Toán lớp 8 tập 2

Câu hỏi:

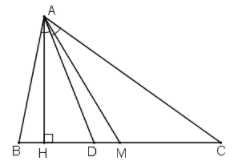
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.

Lời giải:

+ Nhận xét: \(D\) luôn nằm giữa \(H\) và \(M\).

+ Chứng minh:

\(AD\) là đường phân giác của \(∆ABC\).

\(\Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DC}}\) (tính chất đường phân giác của tam giác)

Mà \(AB < AC\) (giả thiết)

\( \Rightarrow DB < DC\) \( \Rightarrow  DB + DC < DC + DC\)

\( \Rightarrow BD + DC < 2DC\) hay \(BC < 2DC\) 

\( \Rightarrow  DC >\dfrac{{BC}}{2}\)

Mà \(MC = \dfrac{{BC}}{2}\) (\(M\) là trung điểm của \(BC\))

\( \Rightarrow DC > MC\) \( \Rightarrow M \) nằm giữa \(D\) và \(C\) (1)

+ Mặt khác: \(\widehat {CAH} = {90^0} - \hat C\) (\(∆CAH\) vuông tại \(H\))

\(\hat A + \hat B + \hat C = {180^0}\) (tổng 3 góc ∆ABC)

\( \Rightarrow \widehat {CAH} = \dfrac{{\widehat A + \widehat B + \widehat C}}{2} - \widehat C\)

\( \Rightarrow \widehat {CAH} = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B}}{2} - \dfrac{{\widehat C}}{2}\)\(\, = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B - \widehat C}}{2}\)

Vì \(AB < AC\) \( \Rightarrow \widehat C < \widehat B\) ( quan hệ giữa cạnh và góc đối diện trong tam giác)

\(\Rightarrow \frac{\widehat B - \widehat C}{2} > 0\)

Do đó: \(\widehat {CAH} >  \dfrac{{\widehat A}}{2}\) hay \(\widehat {CAH} > \widehat {CAD}\)

\( \Rightarrow \) Tia \(AD\) nằm giữa hai tia \(AH\) và \(AC\)

Do đó \(D\) nằm giữa hai điểm \(H\) và \(C\) (2)

Từ (1) và (2) suy ra \(D\) nằm giữa \(H\) và \(M.\)

Bài 58 trang 92 SGK Toán lớp 8 tập 2

Câu hỏi:

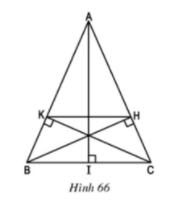
Cho tam giác cân \ (ABC (AB = AC) \), vẽ các đường cao \ (BH, CK \) (H.66).

a) Chứng minh BK = CH.

b) Chứng minh KH // BC.

c) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.

Phương pháp:

Áp dụng: Tính chất tam giác cân, định lý TaLet đảo, tính chất trực tiếp, tính chất hai giác đồng dạng.

Lời giải:

a. Xem hai tam giác vuông \ (BKC \) và \ (CHB \) có:

\ (\ widehat {KBC} = \ widehat {HCB} \) (\ (∆ABC \) cân tại \ (A \))

\ (BC \) is cạnh chung 

\ (\ Mũi tên phải ∆BKC = ∆CHB \) (cạnh huyền - góc nhọn)

\ (\ Rightarrow BK = CH \) (2 cạnh tương ứng)

b. Ta có: \ (AK = AB - BK, AH = AC - HC \) (gt)

Mà \ (AB = AC \) (\ (∆ABC \) cân tại \ (A \))

      \ (BK = CH \) (chứng minh trên) 

\ (\ Rightarrow AK = AH \)

Do đó: \ (\ dfrac {{AK}} {{AB}} = \ dfrac {{AH}} {{AC}} \) \ (\ Rightarrow KH // BC \) (định lí Ta lét đảo)

Bài 59 trang 92 SGK Toán lớp 8 tập 2

Câu hỏi:

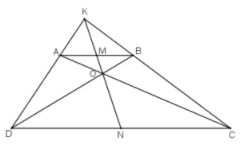
Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD. 

Lời giải:

Qua \(O\) kẻ đường thẳng song song với \(AB, CD\) cắt \(AD, BC\) lần lượt tại \(E, F\).

Suy ra \(AB//EF//CD\)

Gọi N là giao của KO và AB, M là giao của KO với DC.

Ta có: \(OE // DC\) (gt) 

\( \Rightarrow \dfrac{{OE}}{{DC}} = \dfrac{{AO}}{{AC}}\left( 1 \right)\) (hệ quả của định lí TaLet)

\(OF // DC\) (gt)

\( \Rightarrow \dfrac{{OF}}{{DC}} = \dfrac{{BF}}{{BC}}\left( 2 \right)\) (hệ quả của định lí TaLet)

\(OF // AB\) (gt)

\( \Rightarrow \dfrac{{BF}}{{BC}} = \dfrac{{OA}}{{AC}}\) (3) (hệ quả của định lí TaLet)

Từ (1), (2) và (3) ta có: 

\(\dfrac{{OE}}{{DC}} = \dfrac{{OF}}{{DC}} \Rightarrow OE = OF\)

Ta có: \(AB//EF\) (gt) áp dụng hệ quả của định lí TaLet ta có: 

\(\begin{array}{l}
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{KN}}{{K{\rm{O}}}};\,\dfrac{{BN}}{{F{\rm{O}}}} = \dfrac{{KN}}{{K{\rm{O}}}}\\
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{BN}}{{F{\rm{O}}}} \\\text{Mà  } EO=FO\\ \Rightarrow AN = BN
\end{array}\)

\( \Rightarrow \) \(N\) là trung điểm của \(AB.\)

Tương tự ta có: \(EF // DC\) (gt) áp dụng hệ quả của định lí TaLet ta có:

\(\begin{array}{l}
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{KO}}{{K{\rm{M}}}};\,\dfrac{{FO}}{{C{\rm{M}}}} = \dfrac{{KO}}{{K{\rm{M}}}}\\
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{FO}}{{C{\rm{M}}}}\\\text{Mà  }EO=FO\\ \Rightarrow DM = CM
\end{array}\)

\( \Rightarrow M\) là trung điểm của \(CD\).

Vậy \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\). 

Bài 60 trang 92 SGK Toán lớp 8 tập 2

Câu hỏi:

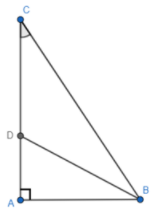
Cho tam giác vuông \(ABC\), \(\widehat A =90^0, \widehat C=30^0\) và đường phân giác \(BD\) (\(D\) thuộc cạnh \(AC\)). 

a) Tính tỉ số \(\dfrac{{A{\rm{D}}}}{{C{\rm{D}}}}\) .

b) Cho biết độ dài \(AB = 12,5 cm\). Hãy tính chu vi và diện tích của tam giác \(ABC\).

Lời giải:

a) Xét tam giác \(BCA\) vuông tại \(A\) (gt) có: 

\(\begin{array}{l}
\widehat {ACB} + \widehat {ABC} = {90^0}\\
\Rightarrow \widehat {ABC} = {90^0} - \widehat {ACB} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {90^0} - {30^0} = {60^0}
\end{array}\)

Trên tia đối của tia \(AB\) lấy điểm \(B'\) sao cho \(AB = AB'\) (1)

Xét hai tam giác vuông \(ABC\) và \(AB'C\) có:

\(AC\) chung (gt)

\(AB = AB'\) (gt)

\( \Rightarrow \Delta ABC = \Delta AB'C\) (cạnh góc vuông - cạnh góc vuông)

\( \Rightarrow BC = B'C\) (2 cạnh tương ứng)

\( \Rightarrow \Delta BB'C\) cân tại \(C\).

Lại có \(\widehat {ABC} = {60^0}\) nên suy ra \(\Delta BB'C\) đều (dấu hiệu nhận biết tam giác đều) (2)

Từ (1) và (2) \( \Rightarrow \dfrac{{AB}}{{BC}} =\dfrac{{AB}}{{BB'}}= \dfrac{1}{2}\)

Vì \(BD\) là đường phân giác của \(\Delta ABC\) nên:

\(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{BC}} = \dfrac{1}{2}\)

b) \(∆ABC\) vuông tại \(A\) nên áp dụng định lí Pitago ta có:

\(\eqalign{
& A{C^2} = B{C^2} - A{B^2},\,BC = 2AB \cr
& \Rightarrow A{C^2} = 4A{B^2} - A{B^2} = 3A{B^2} \cr
& \Rightarrow AC = \sqrt {3A{B^2}} = AB\sqrt 3 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12,5\sqrt 3 \approx 21,65\,cm \cr} \)

Gọi \(p\) là chu vi \(∆ABC\)

\( \Rightarrow p = AB + BC + CA\)

\( \Rightarrow p = 3AB + AC = 3.12,5 + 12,5\sqrt 3 \)

\( \Rightarrow p = 12,5 (3+\sqrt 3 ) \approx 59,15\left( {cm} \right)\)

\({S_{ABC}} = \dfrac{1 }{ 2}AB.AC \approx 135,31(c{m^2})\)

Bài 61 trang 92 SGK Toán lớp 8 tập 2

Câu hỏi:

Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường chéo BD = 10cm.

Lời giải:

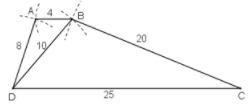
a) Cách vẽ:

- Vẽ \(ΔBDC\):

   + Vẽ \(DC = 25cm\)

   + Vẽ cung tròn tâm \(D\) có bán kính \(10cm\) và cung tròn tâm \(C\) có bán kính \(20cm\). Giao điểm của hai cung tròn là \( B\).

- Vẽ điểm A: Vẽ cung tròn tâm \(B\) có bán kính \( 4cm\) và cung tròn tâm \(D\) có bán kính \( 8cm\). Giao điểm của hai cung tròn này là điểm \(A\). Nối các cạnh BD, BC, DA, BA. 

Vậy là ta đã vẽ được tứ giác \(ABCD\) thỏa mãn điều kiện đề bài.

b) Ta có: \(\dfrac{{AB}}{{BD}} = \dfrac{4}{{10}} = \dfrac{2}{5};\) \(\dfrac{{BD}}{{DC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5};\) \(\dfrac{{AD}}{{BC}} = \dfrac{8}{{20}} = \dfrac{2}{5}\)

\( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{BC}}\)

\(\Rightarrow \Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\left( {c - c - c} \right)\)

c) \(∆ABD∽ ∆BDC\) (chứng minh trên)

\(\Rightarrow \widehat {ABD} = \widehat {BDC}\), mà hai góc ở vị trí so le trong.

\(\Rightarrow AB // DC\) hay \(ABCD\) là hình thang.

Sachbaitap.com