Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 trang 103 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho hai đường tròn (O; 5 cm), (O’; 4 cm) với OO’ = 9 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn?

A. Hai đường tròn cắt nhau.

B. Hai đường tròn ở ngoài nhau.

C. Hai đường tròn tiếp xúc ngoài.

D. Hai đường tròn tiếp xúc trong.

Phương pháp:

Dựa vào kiến thức về vị trí của hai đường tròn.

Lời giải:

Đáp án đúng là: C

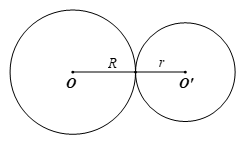
Ta có: 9 = 5 + 4 nên OO’ = R + r, suy ra hai đường tròn (O; 5 cm) và (O’; 4 cm) tiếp xúc ngoài.

Bài 2 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho đường tròn (O; 6 cm) và đường thẳng a với khoảng cách từ O đến a là 4 cm. Kết luận nào sau đây đúng về vị trí giữa đường tròn (O) và đường thẳng a?

A. (O) và a cắt nhau tại hai điểm.

B. (O) và a tiếp xúc.

C. (O) và a không có điểm chung.

D. (O) và a có duy nhất điểm chung.

Phương pháp:

Dựa vào kết quả:

+ Đường thẳng a và đường tròn (O;R) không giao nhau khi d > R.

+ Đường thẳng a tiếp xúc với đường tròn (O; R) khi d = R.

+ Đường thẳng a cắt đường tròn (O;R) khi d < R.

Lời giải:

Đáp án đúng là: A

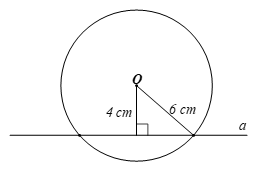
Ta có d = 4 cm, R = 6 cm.

Vì d < R nên đường thẳng a cắt đường tròn (O; 6 cm) tại hai điểm.

Bài 3 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo

Góc ở tâm là góc

A. có đỉnh nằm trên đường tròn

B. có đỉnh nằm trên bán kính của đường tròn.

C. có hai cạnh là hai đường kính của đường tròn.

D. có đỉnh trùng tâm đường tròn.

Phương pháp:

Dựa vào định nghĩa: Góc ở tâm là góc có đỉnh trùng tâm đường tròn.

Lời giải:

Đáp án đúng là: C

Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.

Bài 4 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hình nào dưới đây biểu diễn góc nội tiếp?

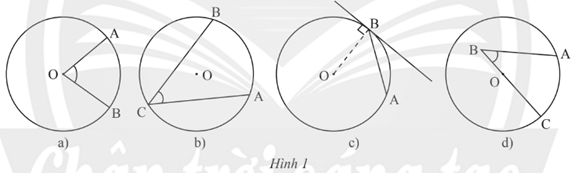
A. Hình 1a

B. Hình 1b

C. Hình 1ca

D. Hình 1d

Phương pháp:

Dựa vào định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Lời giải:

Đáp án đúng là: B

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Vậy hình 1b là hình biểu diễn góc nội tiếp.

Bài 5 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo

Góc nội tiếp chắn nửa đường tròn có số đo là:

A. 180^o

B. 120^o

C. 90^o

D. 60^o

Phương pháp:

Dựa vào Góc nội tiếp chắn nửa đường tròn là góc vuông

Lời giải:

Đáp án đúng là: C

Góc nội tiếp chắn nửa đường tròn là góc vuông.

Bài 6 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M (Hình 2). Biết \(\widehat {AMB} = {50^o}\). Số đo cung nhỏ AB là:

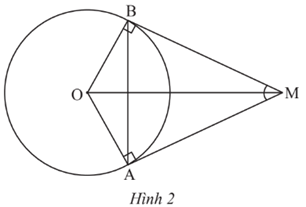
A. 140^o

B. 230^o

C. 130^o

D. 150^o

Phương pháp:

Dựa vào Góc nội tiếp chắn nửa đường tròn là góc vuông

Lời giải:

Đáp án đúng là: B

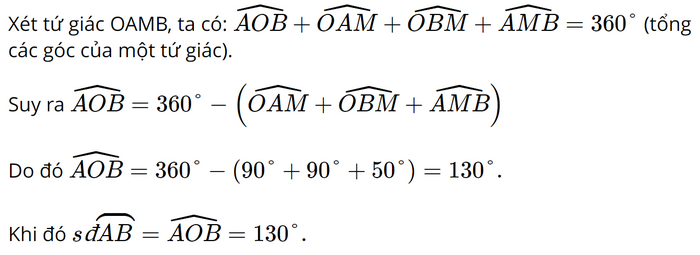
Bài 7 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trong Hình 3, \(\widehat {ACB}\) là góc

A. vuông

B. tù

C. nhọn

D. bẹt

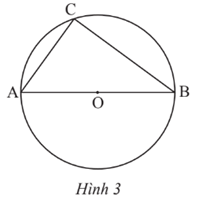
Phương pháp:

Dựa vào: Góc nội tiếp chắn nửa đường tròn là góc vuông

Lời giải:

Đáp án đúng là: A

Vậy độ dài của cạnh NP của tam giác MNP khoảng 18,9 cm.

Bài 8 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trong một đường tròn, khẳng định nào sau đây là sai?

A. Các góc nội tiếp chắn nửa đường tròn là góc vuông.

B. Hai góc nội tiếp bằng nhau chắn hai cung bằng nhau.

C. Hai góc nội tiếp cùng chắn một cung thì bằng nhau.

D. Hai góc nội tiếp bằng nhau thì cùng chắn một cung.

Phương pháp:

Dựa vào: Các góc nội tiếp cùng chắn một cùng hoặc chắn các cung bằng nhau thì bằng nhau.

Lời giải:

Đáp án đúng là: D

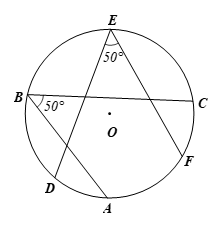
Hai góc nội tiếp bằng nhau nhưng chưa chắc đã cùng chắn một cung.

Chẳng hạn, trong hình vẽ dưới đây,  cùng là hai góc nội tiếp của đường tròn (O) nhưng hai góc này không cùng chắn một cung.

Bài 9 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hình quạt tròn bán kính R, ứng với cung 90^o có diện tích bằng

A. \(\pi {R^2}\)

B. \(\frac{{\pi {R^2}}}{2}\)

C. \(\frac{{\pi {R^2}}}{4}\)

D. \(\frac{{\pi {R^2}}}{8}\)

Phương pháp:

Dựa vào: Diện tích hình quạt tròn bán kính R, ứng với cung n^o là:\(S = \frac{{\pi {R^2}n}}{{360}}\)

Lời giải:

Đáp án đúng là: C

Diện tích hình quạt tròn bán kính R, ứng với cung 90° là:

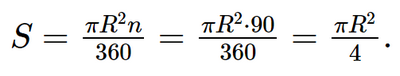
Bài 10 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hình vành khuyên giới hạn bởi hai đường tròn (O; 2 cm) và (O; 4 cm) có diện tích bằng

A. \(12c{m^2}\)

B. \(24c{m^2}\)

C. \(4\pi c{m^2}\)

D. \(12\pi c{m^2}\)

Phương pháp:

Dựa vào: Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O:r) và (O; R) là: \(S = \pi ({R^2} - {r^2})\).

Lời giải:

Đáp án đúng là: D

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 2 cm) và (O; 4 cm) là:

S = π(R² – r²) = π(4² – 2²) = 12π (cm²).

Bài 11 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo

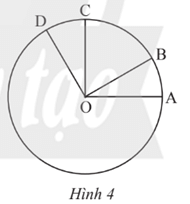
Quan sát Hình 4. Biết \(\widehat {DOA} = {120^o}\), OA \( \bot \)OC, OB \( \bot \)OD.

a) Đọc tên các góc ở tâm có trong hình.

b) Tính số đo của mỗi góc ở tâm tìm được ở câu a

c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180^o

d) So sánh hai cung nhỏ \(\overset\frown{AB}\) và \(\overset\frown{CD}\).

Phương pháp:

Dựa vào: Góc ở tâm là góc có đỉnh trùng với tâm đường tròn, dựa vào hình để xác định góc.

Lời giải:

Bài 12 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo

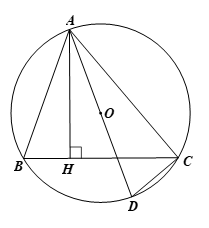
Cho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng

a) AC vuông góc với DC

b) \(\widehat {ABC} = \widehat {ADC}\)

c) AB. AC = AH. AD

Phương pháp:

Đọc kĩ dữ liệu để vẽ hình.

a) Dựa vào: Góc nội tiếp chắn nửa đường tròn là góc vuông

b) Dựa vào: Hai góc nội tiếp cùng chắn một cung thì bằng nhau.

c) Chứng minh \(\Delta \)ABH \(\backsim \)\(\Delta \)ADC (g.g)

Lời giải:

Bài 13 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hãy hoàn thành bảng số liệu sau và vở (lấy \(\pi \approx 3,14\) và làm tròn kết quả đến hàng phần mười)

Phương pháp:

Dựa vào công thức: \(l = \frac{{\pi Rn}}{{180}}\)

Lời giải:

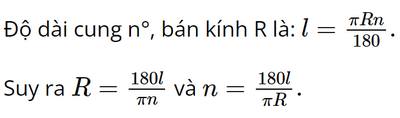
Áp dụng các công thức trên, ta hoàn thành được bảng đã cho như sau:

Bài 14 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.

a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài B.

b) Gọi H là trung điểm AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.

c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.

d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).

Phương pháp:

Đọc kĩ dữ liệu để vẽ hình.

a) Dựa vào: Vị trí tương đối của hai đường tròn để chứng minh

b) Chứng minh tứ giác ADCE là hình bình hành có AC\( \bot \)DE nên ADCE là hình thoi.

c) Chứng minh EB và FB trùng nhau nên ba điểm F, B, E thẳng hàng.

d) Chứng minh HF\( \bot \)O’F và F thuộc (O’) nên HF là tiếp tuyến của đường tròn (O’).

Lời giải:

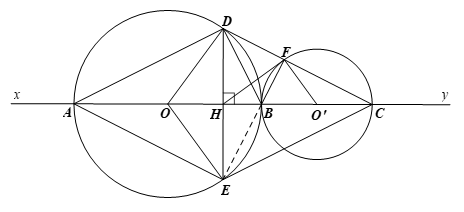
a) Ta có OO’ = OB + BO’ nên đường tròn (O) và (O’) tiếp xúc ngoài tại B.

b) Xét ∆ODE có OD = OE (cùng là bán kính của đường tròn (O) đường kính AB) nên ∆ODE cân tại O. Do đó đường cao OH đồng thời là đường trung tuyến của tam giác hay H là trung điểm của DE.

Xét tứ giác ADCE có hai đường chéo AC và DE cắt nhau tại trung điểm H của mỗi đường nên ADCE là hình bình hành.

Lại có DE ⊥ AC tại H nên hình bình hành ADCE là hình thoi.

Lại có AD // CE (do ADCE là hình thoi) nên DB ⊥ CE.

Xét ∆CDE có DB, CH là hai đường cao của tam giác cắt nhau tại B (do DB ⊥ CE và CH ⊥ DE) nên B là trực tâm của ∆CDE. Suy ra EF ⊥ CD. (1)

Xét đường tròn (O’) có HF ⊥ O’F tại F thuộc đường tròn nên HF là tiếp tuyến của đường tròn (O’).

Bài 15 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hải đăng Kê Gà tọa lạc tại xã Tân Thành, huyên Hàm Thuận Nam, tỉnh Bình Thuận. Biết ngọn hải đăng cao 65 m so với mặt nước biển. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng này?

Cho biết mắt người quan sát ở độ cao 5 m so với mực nước biển và bán kính Trái Đất gần bằng 6400 km.

Phương pháp:

Chứng minh \(\Delta \)CHB \(\backsim \) \(\Delta \)HDB (g.g) và \(\Delta \)FHA \(\backsim \) \(\Delta \)HEA (g.g) rồi suy ra tỉ số đồng dạng để tính.

Lời giải:

Gọi R là bán kính Trái Đất, khi đó R ≈ 6 400 km.

Đổi 65 m = 0,065 km; 5 m = 0,005 km.

Ta có: OA = R + 0,065 ≈ 6 400 + 0,065 = 6 400,065 (km).

OB = R + 0,005 ≈ 6 400 + 0,005 = 6 400,005 (km).

Xét ∆OHA vuông tại H, theo định lí Pythagore, ta có: OA² = OH² + AH²

Suy ra AH² = OA² – OH² ≈ 6 400,065² – 6 400² = 832,004225.

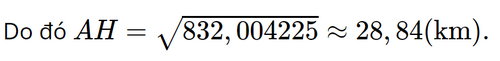
Xét ∆OHB vuông tại H, theo định lí Pythagore, ta có: OB² = OH² + BH²

Suy ra BH² = OB² – OH² ≈ 6 400,005² – 6 400² = 64,000025.

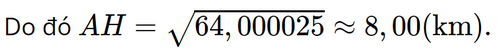
Ta có AB = AH + HB ≈ 28,84 + 8 = 36,84 (km).

Vậy với khoảng cách khoảng 36,84 kilômét thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng.

Sachbaitap.com