Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 88 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 88 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} = {130^o}\). Tính số đo \(\widehat {CMB}\) .

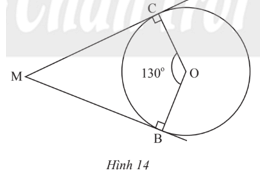
Phương pháp:

Tính \(\widehat {CMB}\) bằng cách dựa vào tính chất trong một tứ giác tổng các góc bằng 360^o.

Lời giải:

Bài 2 trang 88 SGK Toán 9 tập 1 - Chân trời sáng tạo

Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x.

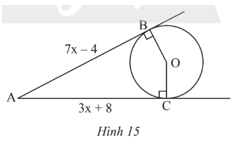
Phương pháp:

Chứng minh hai tam giác ABO = tam giác ACO theo cạnh góc cạnh. Sau đó suy ra AB = AC để tìm x.

Lời giải:

Ta có AB, AC là hai tiếp tuyến của đường tròn (O) cắt nhau tại A nên AB = AC hay 7x – 4 = 3x + 8.

Giải phương trình:

7x – 4 = 3x + 8

4x = 12

  x = 3.

Vậy x = 3.

Bài 3 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trong Hình 16, AB = 9; BC = 12; AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).

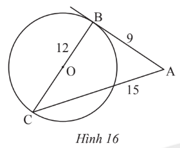
Phương pháp:

Chứng minh \(\widehat {CBA} = {90^o}\) hay \(AB \bot BO\) suy ra AB là tiếp tuyến.

Lời giải:

Xét ∆ABC có:

⦁ AB² + BC² = 9² + 12² = 225;

⦁ AC² = 15² = 225.

Do đó AB² + BC² = AC²,

Theo định lí Pythagore đảo, ta có ∆ABC vuông tại B.

Suy ra AB ⊥ BC hay AB ⊥ OB.

Xét đường tròn (O) có AB ⊥ OB tại B thuộc đường tròn (O) nên AB là tiếp tuyến của đường tròn (O).

Bài 4 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho tam giác ABC có đương tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm; BP = 3 cm; CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.

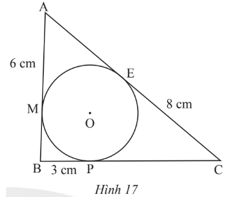
Phương pháp:

- Dựa vào tính chất hai tiếp tuyến cắt nhau để chứng minh BM = BP, AM = AE, CE = CP.

- Tính chu vi tam giác bằng AB + AC + BC.

Lời giải:

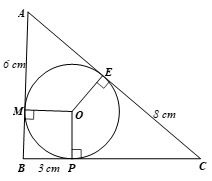
Ta có:

⦁ AE, AM là hai tiếp tuyến của (O) cắt nhau tại A nên AE = AM = 6 cm (tính chất hai tiếp tuyến cắt nhau).

⦁ BM, BP là hai tiếp tuyến của (O) cắt nhau tại B nên BM = BP = 3 cm (tính chất hai tiếp tuyến cắt nhau).

⦁ CP, CE là hai tiếp tuyến của (O) cắt nhau tại C nên CP = CE = 8 cm (tính chất hai tiếp tuyến cắt nhau).

Chu vi tam giác ABC là:

AB + BC + CA = AM + BM + BP + CP + CE + AE

= 6 + 3 + 3 + 8 + 8 + 6 = 34 (cm).

Bài 5 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:

a) \(\widehat {ACB}\) có số đo bằng 90^o, từ đó suy ra độ dài của BC theo R;

b) OM là tia phân giác của \(\widehat {COA}\).

c) MC là tiếp tuyến của đường tròn (O; R).

Phương pháp:

- Dựa vào dữ kiện đề bài để vẽ hình.

- Tính BC bằng cách áp dụng định lý Pythagore trong tam giác vuông ABC rồi rủ BC theo R.

- Chứng minh OI \( \bot \) AC, tam giác OAC là tam giác cân suy ra OI vừa là trung tuyến và vừa phân giác \(\widehat {COA}\) nên OM là tia phân giác của \(\widehat {COA}\).

- Chứng minh tam giác AOM = tam giác OCM suy ra \(\widehat {OAM} = \widehat {OCM} = {90^o}\). Do đó, MC là tiếp tuyến của đường tròn (O; R).

Lời giải:

Bài 6 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho đường tròn (O; 5 cm) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) vuông góc với nhau tại M.

a) Tính độ dài MA và MB.

b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài CD.

Phương pháp:

- Dựa vào dữ kiện đề bài để vẽ hình.

- Chứng minh tứ giác AOBM là hình vuông suy ra đô dài MA và MB.

- Chứng minh OI \( \bot \) AC, tam giác OAC là tam giác cân suy ra OI vừa là trung tuyến và vừa phân giác \(\widehat {COA}\) nên OM là tia phân giác của \(\widehat {COA}\).

- Chứng minh tam giác OCD cân tại O suy ra OI là đường trung tuyến. Áp dụng tỉ số lượng giác trong tam giác CIO ta tính CI suy ra CD.

Lời giải:

Do đó tứ giác OAMB là hình chữ nhật.

Lại có OA = OB = 5 cm (do A, B nằm trên đường tròn (O; 5 cm)).

Suy ra hình chữ nhật OAMB là hình vuông, nên MA = MB = OA = OB = 5 cm.

Vậy CD = CI + DI = 5 + 5 = 10 (cm).

Bài 7 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho đường tròn (O) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) thoả mãn \(\widehat {AMB} = {60^o}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.

Phương pháp:

- Dựa vào dữ kiện đề bài để vẽ hình.

- Chứng minh tam giác AOM = tam giác BMO. Suy ra MA = MB thì tam giác AMB cân tại M

- Chứng minh tam giác AMB đều suy ra độ dài AB từ chu vi tam giác MAB.

Lời giải:

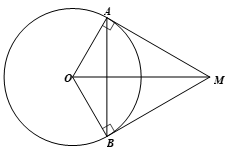
Vì MA và MB là hai tiếp tuyến tại A, B của đường tròn (O) cắt nhau tại M nên MA = MB (tính chất hai tiếp tuyến cắt nhau).

Do đó ∆MAB cân tại M, lại có 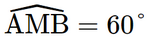nên ∆MAB là tam giác đều.

Suy ra MA = MB = AB.

Chu vi ∆MAB là: MA + MB + AB = 3AB.

Theo bài, chu vi tam giác MAB là 18 cm nên 3AB = 18, do đó AB = 6 (cm).

Vậy AB = 6 cm.

Bài 8 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo

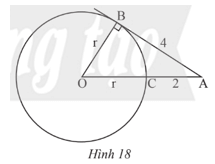
Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.

a) Tính bán kính r của đường tròn (O).

b) Tính chiều dài cạnh OA của tam giác ABO.

Phương pháp:

- Áp dụng định lý Pythagore trong tam giác vuông OAB ta có hệ thức theo r rồi tính r.

- Thay r từ đó ta tính cạnh OA.

Lời giải:

a) Vì AB là tiếp tuyến của đường tròn (O) tại B nên AB ⊥ OB tại B.

Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có: OA² = OB² + AB²

Suy ra (OC + CA)² = OB² + AB²

Do đó (r + 2)² = r² + 4². (*)

Giải phương trình (*):

(r + 2)² = r² + 4²

r² + 4r + 4 = r² + 16

4r = 12

r = 3.

Vậy bán kính của đường tròn (O) là r = 3.

b) Ta có OA = OC + CA = r + 2 = 3 + 2 = 5 (cm).

Vậy OA = 5 cm.

Sachbaitap.com