Giải bài 9.11, 9.12, 9.13, 9.14, 9.15, 9.15 trang 92 SGK Toán 8 Kết nối tri thức tập 2
Giải sách giáo khoa Toán lớp 8 trang 92 Kết nối tri thức với cuộc sống tập 2: bài 9.11, 9.12, 9.13, 9.14, 9.15, 9.15. Cho ΔABC ∽ ΔA'B'C'. Biết AB=3cm, A′B′=6cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'
Bài 9.11 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức
Cho ΔABC ∽ ΔDEF. Biết \(\widehat A = {60^o};\widehat E = {80^o}\), hãy tính số đo các góc \(\widehat B,\widehat C,\widehat D,\widehat F\)
Phương pháp:
- Sử dụng ΔABC ∽ ΔDEF suy ra \(\widehat A = \widehat D{,^{}}\widehat B = \widehat E{,^{}}\widehat C = \widehat F\).
- Từ đó tính các góc \(\widehat B,\widehat C,\widehat D,\widehat F\)
Lời giải:
Vì ΔABC ∽ ΔDEF. Suy ra 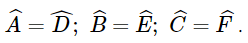
Mà 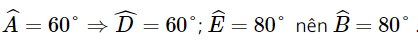
Có 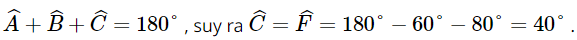
Bài 9.12 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức
Cho ΔABC ∽ ΔA'B'C'. Biết AB=3cm, A′B′=6cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'
Phương pháp:
- Từ ΔABC ∽ ΔA'B'C' tính được tỉ số đồng dạng.
Suy ra chu vi tam giác A’B’C’.
Lời giải:
Vì ΔABC ∽ ΔA'B'C' nên 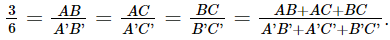
Suy ra A'B' + A'C' + B'C' = 2(AB + AC + BC) = 2 . 10 = 20 (cm).
Vậy chu vi tam giác A'B'C' là 20 cm.
Bài 9.13 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức
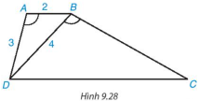
Cho hình thang ABCD (AB // CD) có \(\widehat {DAB} = \widehat {DBC}\)
a) Chứng minh rằng ΔABD ∽ ΔBDC
b) Giả sử AB=2cm,AD=3cm,BD=4cm. Tính độ dài các cạnh BC và DC
Phương pháp:
a) Chứng minh ΔABD ∽ ΔBDC (g.g)
b) Tính tỉ số đồng dạng của tam giác ABD và tam giác BDC. Từ đó tính độ dài của DC, BC
Lời giải:
a) Vì AB // CD (giả thiết) nên 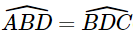 (2 góc ở vị trí so le trong).
(2 góc ở vị trí so le trong).
+ Xét ΔABD và ΔBDC có: 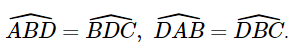 .
.
Suy ra ΔABD ∽ ΔBDC (g.g).
b) Ta có: 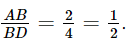 .
.
Vậy ΔABD ∽ ΔBDC với tỉ số đồng dạng 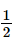 .
.
Suy ra 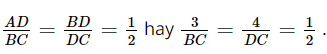 .
.
Suy ra BC = 2 . 3 = 6 cm; DC = 4 . 2 = 8 cm.
Bài 9.14 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức
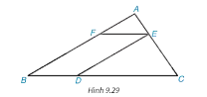
Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE=4cm, AB=6cm. Chứng minh rằng ΔAEF ∽ ΔECD và tính tỉ số đồng dạng
Phương pháp:
Áp dụng tính chất hai đường thẳng song song => Các cặp góc bằng nhau
=> Hai tam giác đồng dạng, ta có tỉ số đồng dạng
Lời giải:
- Có EF // BC. Suy ra 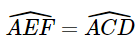 (2 góc đồng vị). (1)
(2 góc đồng vị). (1)
- Có EF // BD (vì EF // BC) và DE // FB (vì ED // AB).
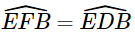 .
.Mà 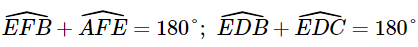 (kề bù).
(kề bù).
Do đó, 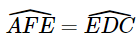 . (2)
. (2)
Từ (1) và (2) suy ra ΔAEF ∽ ΔECD (g.g).
Vì EFBD là hình bình hành nên BF = ED = 4 cm.
Mà AF + BF = AB nên AF = AB – BF = 6 – 4 = 2
Khi đó, 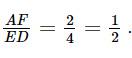
Vậy ΔAEF ∽ ΔECD với tỉ số đồng dạng là 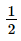
Bài 9.15 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức
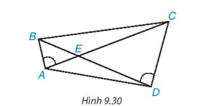
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat {BAC} = \widehat {C{\rm{D}}B}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Phương pháp:
- Chứng minh\(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
- Chứng minh ΔAED ∽ ΔBEC (c.g.c)
Lời giải:
Xét ΔAEB và ΔDEC có:
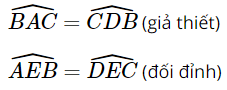
Suy ra ΔAEB ∽ ΔDEC (g.g).
Suy ra 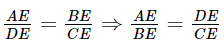
Xét ΔAED và ΔBEC có:
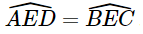 (2 góc đối đỉnh)
(2 góc đối đỉnh)
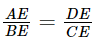 (chứng minh trên)
(chứng minh trên)
Suy ra ΔAED ∽ ΔBEC (c.g.c).
Bài 9.16 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức
Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM=MD, 2BN=NC. Biết AB=5cm,CD=6cm. Hãy tính độ dài đoạn thẳng MN
Phương pháp:
Gọi I là giao điểm của AC và MN
Sử dụng các tam giác đồng dạng để tính độ dài MI, IN. Từ đó tính độ dài đoạn MN.
Lời giải:
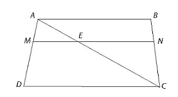
Vẽ đường thẳng qua M song song với CD cắt AC tại E.
Khi đó: 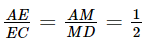 (định lí Thalès).
(định lí Thalès).
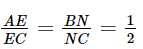 (2BN = NC), suy ra NE // AB (định lí Thalès đảo).
(2BN = NC), suy ra NE // AB (định lí Thalès đảo).Ta có:
ME // CD
NE // AB
AB // CD
Do đó ME // CD và NE // CD, suy ra M, N, E thẳng hàng.
Mặt khác ∆AME ∽ ∆ADC (vì ME // CD).
Nên 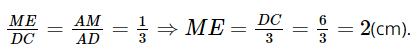
Tương tự ∆CEN ∽ ∆CAB (vì NE //AB) nên 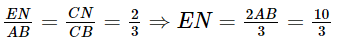 (cm).
(cm).
Vậy MN = ME + EN = 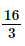 (cm).
(cm).
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,15 trang 135,136 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.15, 10.16, 10.17, 10.18, 10.19, 10.20, 10.21, 10.22, 10.23, 10.24 trang 123, 124 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.11, 10.12, 10.13, 10.14 trang 121, 122 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.5, 10.6, 10.7, 10.8, 10.9, 10.10 trang 120 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Giải bài 10.1, 10.2, 10.3, 10.4 trang 116 SGK Toán 8 Kết nối tri thức tập 2 (07/12)
- Bài tập ôn tập cuối năm
- Bài tập cuối chương 10
- Luyện tập chung (trang 121)
- Bài 39. Hình chóp tứ giác đều
- Bài 38. Hình chóp tam giác đều
- CHƯƠNG X. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
- Bài tập cuối chương 9
- Luyện tập chung (trang 108)
- Bài 37.Hình đồng dạng
- Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
