Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
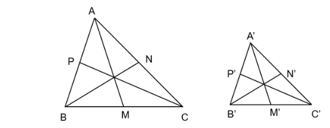
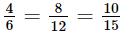Vì ΔA′B′C′ ∽ ΔABC nên: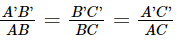
; (1)
và 
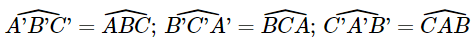. (2)
Hai tam giác A'B'M' và ABM có:
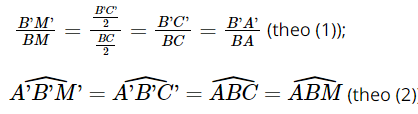
Do đó ΔA′M′B′ ∽ ΔAMB (c.g.c). Suy ra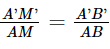 
(3).
Tương tự ΔA′C′P′ ∽ ΔACP và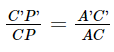 
(4).
ΔA′B′N′ ∽ ΔABN và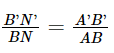 
(5).
Từ (1), (3), (4) và (5) suy ra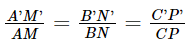 
Bài 9.8 trang 90 SGK Toán 8 tập 2 - Kết nối tri thức
Cho tam giác ABC có AB=12cm, AC=15cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM=10cm, AN=8cm. Chứng minh rằng ΔABC ∽ ΔANM.
Phương pháp:
- Chứng minh: \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\)
- Chứng minh hai tam giác ABC và tam giác ANM có hai cạnh tương ứng tỉ lệ và góc A chung nên hai tam giác ABC và tam giác ANM đồng dạng với nhau.
Lời giải:
Có AB = 12 cm , AN = 8 cm. Suy ra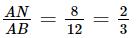 
AC = 15 cm, AM = 10 cm. Suy ra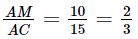 
Suy ra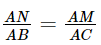 
.
Xét hai tam giác ABC và tam giác ANM có:
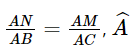chung.
Do đó ΔABC ∽ ΔANM (c.g.c)
Bài 9.9 trang 90 SGK Toán 8 tập 2 - Kết nối tri thức
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat {ABN} = \widehat {ACM}\)
a) Chứng minh rằng ΔABN ∽ ΔACM
b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN=IC.IM
Phương pháp:
a) Chứng minh: tam giác ABN và tam giác ACM
có góc A chung, \(\widehat {ABN} = \widehat {ACM}\)
=> ΔABN ∽ ΔACM
b) Chứng minh: ΔIBM ∽ ΔICN (g.g) nên suy ra các tỉ số đồng dạng
Lời giải:
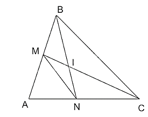
a) Xét tam giác ABN và tam giác ACM:
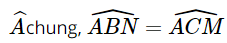(giả thiết)
Suy ra ΔABN ∽ ΔACM (g.g).
b) Vì ΔABN ∽ ΔACM (chứng minh trên) nên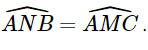 
Lại có: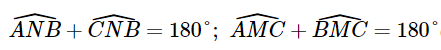 
(kề bù), suy ra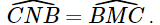 
Xét tam giác IBM và tam giác ICN có:
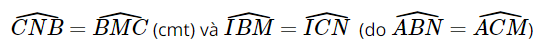
Suy ra ΔIBM ∽ ΔICN (g.g).
Suy ra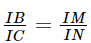 
. Suy ra IB . IN = IC . IM.
Bài 9.10 trang 90 SGK Toán 8 tập 2 - Kết nối tri thức
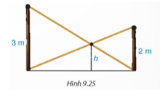
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.
Phương pháp:
- Theo đề bài vẽ lại hình và đặt tên các điểm.
- Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để tính độ cao của h
Lời giải:
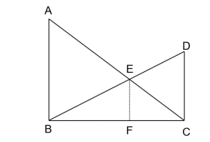
Kí hiệu các điểm như hình vẽ trên.
Do đó ΔCEF ∽ ΔCAB và ΔBEF ∽ ΔBDC.
Suy ra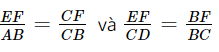
.
Do đó: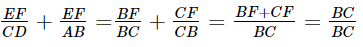
Suy ra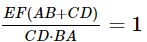
Vậy h=EF=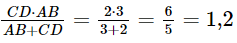 
(m).
Sachbaitap.com
