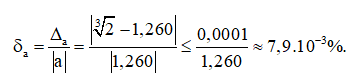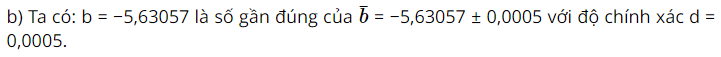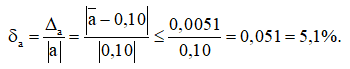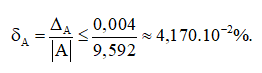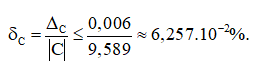Giải SBT Toán 10 trang 113, 114 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 113, bài 8, 9 trang 114 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 1. Trong các số sau, số nào là số gần đúng?
Bài 1 trang 113 SBT Toán 10 - Chân trời sáng tạo
Trong các số sau, số nào là số gần đúng?
a) Dân số Việt Nam năm 2020 là 97,34 triệu người.
b) Số gia đình văn hóa ở khu phố mới là 45
c) Đường bờ biển Việt Nam dài khoảng 3260km.
d) Vào năm 2022, Việt Nam có 63 tỉnh thành, thành phố trực thuộc trung ương.
Lời giải:
Trong các số ở các trường hợp a), b), c), d) thì các số 97,34 và 3 260 là số gần đúng. Vì không thể xác định được dân số cụ thể của Việt Nam năm 2020 và chiều dài cụ thể của đường bờ biển Việt Nam.
Bài 2 trang 113 SBT Toán 10 - Chân trời sáng tạo
Viết số quy tròn của mỗi số sau với độ chính xác \(d\).
a) \(a = 0,012345679\) với \(d = 0,001\)
b) \(b = - 1737,183\) với \(d = 0,01\)
c) \(c = 456572\) với \(d = 1000\)
Phương pháp:
Dùng quy tắc làm tròn số và xác định số quy tròn của số gần đúng theo độ chính xác cho trước.
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của \(d\).
Bước 2: Quy tròn số \(a\)ở hàng gấp 10 lần hàng tìm được ở Bước 1.
Lời giải:
a) Xét d = 0,001 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,001 là hàng phần nghìn nên ta quy tròn số a ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần trăm.
Xét chữ số ở hàng phần nghìn của a là 2, là số bé hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần trăm là 0,01.
b) Xét d = 0,01 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần trăm. Nên suy ra hàng lớn nhất của độ chính xác d = 0,01 là hàng phần trăm, nên ta quy tròn số b ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần mười.
Xét chữ số ở hàng phần trăm của b là 8, là số lớn hơn 5 nên ta suy ra được số quy tròn của b đến hàng phần mười là −1737,2.
c) Xét d = 1 000 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 1 000 là hàng nghìn nên ta quy tròn số c ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng chục nghìn.
Xét chữ số ở hàng nghìn của c là 6, là số lớn hơn 5 nên ta suy ra được số quy tròn của c đến hàng chục nghìn là 460 000.
Bài 3 trang 113 SBT Toán 10 - Chân trời sáng tạo
Cho biết \(\sqrt[3]{2} = 1,25992104989...\)
a) Hãy quy tròn \(\sqrt[3]{2}\)đến hàng phần nghìn và ước lượng sai số tương đối.
b) Hãy tìm số gần đúng của \(\sqrt[3]{2}\)với độ chính xác \(0,00007\)
Phương pháp:
+ Xác định số quy tròn của số gần đúng theo độ chính xác cho trước.
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của \(d\).
Bước 2: Quy tròn số \(a\)ở hàng gấp 10 lần hàng tìm được ở Bước 1.
+ Tìm sai số tuyệt đối từ đó suy ra sai số tương đối.
Lời giải:
Áp dụng công thức ta tính được sai số tương đối của số gần đúng a là
b) Xét d = 0,00007 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần trăm nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,00007 là hàng phần trăm nghìn nên ta quy tròn số a ở hàng vừa tìm được, tức là hàng phần chục nghìn.
Xét chữ số ở hàng phần triệu của a là 1, là số bé hơn 5 nên ta suy ra được số gần đúng của a với độ chính xác d = 0,00007 là 1,25992.
Bài 4 trang 113 SBT Toán 10 - Chân trời sáng tạo
Hãy viết số quy tròn của số gần đúng trong các trường hợp sau:
a) \(37213824 \pm 100\)
b) \( - 5,63057 \pm 0,0005\)
Phương pháp:
Bước 1: Xác định \(a\)và \(d\)trong số đúng \(a \pm d\)
Bước 2: Tìm hàng của chữ số khác 0 đầu tiên bên trái của \(d\).
Bước 3: Quy tròn số \(a\)ở hàng gấp 10 lần hàng tìm được ở Bước 1.
Lời giải:
Xét d = 100 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng trăm. Nên suy ra hàng lớn nhất của độ chính xác d = 100 là hàng trăm nên ta quy tròn số a ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng nghìn.
Xét chữ số ở hàng trăm của a là 8, là số lớn hơn 5 nên ta suy ra được số quy tròn của a đến hàng nghìn là 37 214 000.
Xét d = 0,0005 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần chục nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,0005 là hàng chục nghìn nên ta quy tròn số b ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần nghìn.
Xét chữ số ở hàng phần chục nghìn của b là 5 nên ta suy ra được số quy tròn của b đến hàng phần nghìn là −5,631.
Bài 5 trang 113 SBT Toán 10 - Chân trời sáng tạo
Gọi \(\overline h \)là độ dài đường cao của tam giác đều có cạnh bằng \(6cm\). Tìm số quy tròn của \(h\)với độ chính xác \(d = 0,01\)
Phương pháp:
Tính độ dài đường cao
Dùng quy tắc làm tròn số và xác định số quy tròn của số gần đúng theo độ chính xác cho trước.
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của \(d\).
Bước 2: Quy tròn số \(a\)ở hàng gấp 10 lần hàng tìm được ở Bước 1.
Lời giải:
Bài 6 trang 113 SBT Toán 10 - Chân trời sáng tạo
Cho số gần đúng \(a = 0,1031\)với độ chính xác \(d = 0,002\).
Hãy viết số quy tròn của số \(a\) và ước lượng sai số tương đối của quy tròn đó.
Phương pháp:
+ Dùng quy tắc làm tròn số và xác định số quy tròn của số gần đúng theo độ chính xác cho trước.
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của \(d\).
Bước 2: Quy tròn số \(a\)ở hàng gấp 10 lần hàng tìm được ở Bước 1.
+ Xác định sai số tuyệt đối từ đó suy ra sai số tương đối.
Lời giải:
Xét d = 0,002 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,002 là hàng phần nghìn nên ta quy tròn số a ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần trăm.
Xét chữ số ở hàng phần nghìn của a là 3, là số bé hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần trăm là 0,10.
Áp dụng công thức ta tính được sai số tương đối của số gần đúng a là
Bài 7 trang 113 SBT Toán 10 - Chân trời sáng tạo
Sử dùng cùng lúc 3 thiết bị khác nhau để đo thành tích chạy 100 m của một vận động viên, người ta được kết quả như sau:
|
Thiết bị |
A |
B |
C |
|
Kết quả |
\(9,592 \pm 0,004\) |
\(9,593 \pm 0,005\) |
\(9,589 \pm 0,006\) |
Tính sai số tương đối từng thiết bị. Thiết bị nào có sai số tương đối nhỏ nhất?
Phương pháp:
Bước 1: Tìm sai số tuyệt đối
Bước 2: Ước lượng sai số tương đối
Lời giải:
+) Xét kết quả của thiết bị A. Do ∆A ≤ d = 0,004. Với A = 9,592 là số gần đúng.
Áp dụng công thức ta tính được sai số tương đối của số gần đúng A là
+) Xét kết quả của thiết bị B. Do ∆B ≤ d = 0,005. Với B = 9,593 là số gần đúng.
Áp dụng công thức ta tính được sai số tương đối của số gần đúng B là
+) Xét kết quả của thiết bị C. Do ∆C ≤ d = 0,006. Với C = 9,589 là số gần đúng.
Áp dụng công thức ta tính được sai số tương đối của số gần đúng C là
Vậy suy ra thiết bị A có sai số tương đối nhỏ nhất.
Bài 8 trang 114 SBT Toán 10 - Chân trời sáng tạo
Nam đo được đường kính của một hình tròn là \(24 \pm 0,2\,cm\). Nam tính được chu vi của hình tròn là \(p = 72,36\,cm\). Hãy tính ước lượng sai số tuyệt đối của \(p\), biết \(3,141 < \pi < 3,142\).
Lời giải:
Bài 9 trang 114 SBT Toán 10 - Chân trời sáng tạo
Nhà sản xuất công bố chiều dài và chiều rộng của 1 tấm thép hình chữ nhật lần lượt là \(100 \pm 0,5\,\,cm\) và \(70 \pm 0,5\,\,cm\). Hãy tính diện tích của tám thép.
Lời giải:
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SBT Toán 10 trang 102, 103 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 100, 101 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 95, 96, 97 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 77, 78, 79, 80 Chân trời sáng tạo tập 2 (30/01)
- Giải SBT Toán 10 trang 75, 76 Chân trời sáng tạo tập 2 (30/01)
- Bài tập cuối chương X - SBT Toán 10 CTST
- Bài 2. Xác suất của biến cố - SBT Toán 10 CTST
- Bài 1. Không gian mẫu và biến cố - SBT Toán 10 CTST
- Chương X. Xác suất - SBT Toán 10 CTST
- Bài tập cuối chương IX - SBT Toán 10 CTST
- Bài 4. Ba đường conic trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 3. Đường tròn trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 2. Đường thẳng trong mặt phẳng tọa độ - SBT Toán 10 CTST
- Bài 1. Tọa độ của vectơ - SBT Toán 10 CTST
- Chương IX. Phương pháp tọa độ trong mặt phẳng - SBT Toán 10 CTST
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!