Giải SBT Toán 10 trang 69 Chân trời sáng tạo tập 1

Bài 1 trang 69 SBT Toán 10 - Chân trời sáng tạo

Tính giá trị của \(T = 4\cos 60^\circ  + 2\sin 135^\circ  + 3\cot 120^\circ \)

Lời giải:

Sử dụng máy tính cầm tay ta có:

T = 4cos60° + 2sin135° + 3cot120°

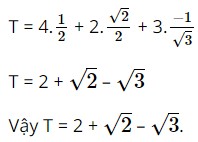
Bài 2 trang 69 SBT Toán 10 - Chân trời sáng tạo

Chứng minh rằng

a) \(\sin 138^\circ  = \sin 42^\circ \) 

b) \(\tan 125^\circ  =  - \cot 35^\circ \)

Phương pháp:

a) \(\sin \alpha  = \sin \left( {180^\circ  - \alpha } \right)\)

b) \(\tan \alpha  =  - \tan \left( {180^\circ  - \alpha } \right)\left( {a \ne 90^\circ } \right)\)

Lời giải:

a) Ta có sinx = sin(180° – x ) nên:

sin138° = sin (180° – 138°) = sin42°.

Vậy sin138° = sin42°.

b) Ta có tanx = –tan(180° – x) và tanx = cot( 90° – x )

tan125 = –tan(180° – 125°) = –tan55° = –cot( 90° – 55° ) = –cot35°.

Vậy tan125° = – cot35°.

Bài 3 trang 69 SBT Toán 10 - Chân trời sáng tạo

Tìm góc \(\alpha \left( {0^\circ  \le \alpha  \le 180^\circ } \right)\) trong mỗi trường hợp sau:

a) \(\cos \alpha  =  - \frac{{\sqrt 3 }}{2}\)

b) \(\sin \alpha  = \frac{{\sqrt 3 }}{2}\)

c) \(\tan \alpha  =  - \frac{{\sqrt 3 }}{3}\)

d) \(\cot \alpha  =  - 1\)

Phương pháp:

Sử dụng máy tính cầm tay hoặc tra bảng giá trị lượng giác của các góc đặc biệt.

Lời giải:

a) Sử dụng máy tính cầm tay, ta có được: α = 150°.

b) Sử dụng máy tính cầm tay, ta có được: α = 60°.

Lại có sinα = sin(180° – α ) nên α = 120°.

Vậy α = 60° hoặc α = 120°.

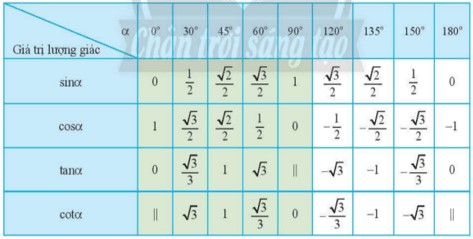
d) Dựa vào bảng các giá trị lượng giác đặc biệt, ta có: cot α = –1 ⇒ α = 135°.

Vậy α = 135°.

Bài 4 trang 69 SBT Toán 10 - Chân trời sáng tạo

Chứng minh rằng trong tam giác ABC ta có:

a) \(\tan B =  - \tan \left( {A + C} \right)\)     

b) \(\sin C = \sin \left( {A + B} \right)\)

Phương pháp:

Dựa vào mối liên hệ giữa các giá trị lượng giác giữa hai góc phụ nhau, bù nhau

Lời giải:

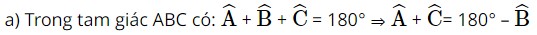
Ta có: tanα = –tan(180° – α ) nên

tanB = –tan( 180° – B ) = –tan( A+C)

Vậy tanB = –tan( A+C).

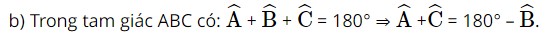
Ta có: sinα = sin(180° – α ) nên

sinC = sin(180° – C ) = sin ( A+B ).

Vậy sinC = sin ( A+B ).

Bài 5 trang 69 SBT Toán 10 - Chân trời sáng tạo

Chứng minh rằng với mọi góc \(x\left( {0^\circ  \le x \le 90^\circ } \right)\), ta đều có:

a) \(\sin x = \sqrt {1 - {{\cos }^2}x} \) 

b) \(\cos x = \sqrt {1 - {{\sin }^2}x} \)

c) \({\tan ^2}x = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}\left( {x \ne 90^\circ } \right)\)               d) \({\cot ^2}x = \frac{{{{\cos }^2}x}}{{{{\sin }^2}x}}\left( {x \ne 0^\circ } \right)\)

Lời giải:

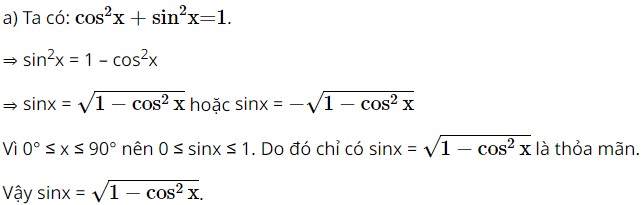
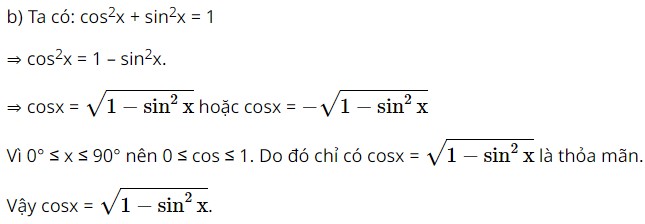
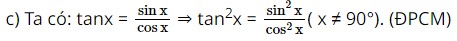
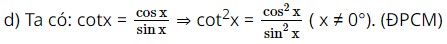
Bài 6 trang 69 SBT Toán 10 - Chân trời sáng tạo

Cho góc x với \(\cos x =  - \frac{1}{2}\). Tính giá trị của biểu thức \(S = 4{\sin ^2}x + 8{\tan ^2}x\)

Lời giải:

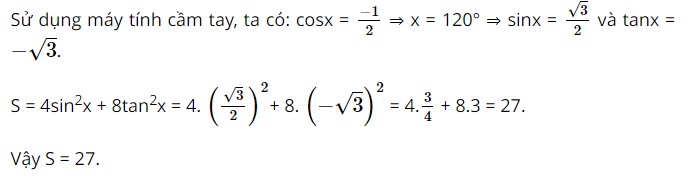
Bài 7 trang 69 SBT Toán 10 - Chân trời sáng tạo

Dùng máy tính cầm tay, tính:

a) \(\sin 130^\circ 12'24''\)   

b) \(\cos 144^\circ 35'12''\)

c) \(\tan 152^\circ 35'44''\)

Lời giải:

Sử dụng máy tính cầm tay, ta tính được:

a) sin138°12’24’’ ≈ 0,666.

b) cos144°35’12’’≈ –0,815.

c) tan152°35’44’’ ≈ –0,518.

Bài 8 trang 69 SBT Toán 10 - Chân trời sáng tạo

Dùng máy tính cầm tay, tìm x biết:

a) \(\cos x =  - 0,234\) 

b) \(\sin x = 0,812\)   

c) \(\cot x =  - 0,333\)

Lời giải:

Sử dụng máy tính cầm tay, ta tính được:

a) cosx = –0,234 ⇒ x ≈ 103°31’58’’.

b) sinx = 0,812 ⇒ x ≈ 54°17’30’’ hay x ≈ 125°42’30’’.

c) cotx = –0,333 ⇒ x ≈ 108°25’4’’. 

Sachbaitap.com