Giải SBT Toán 10 trang 74, 75 Chân trời sáng tạo tập 1

Bài 1 trang 74 SBT Toán 10 - Chân trời sáng tạo

Tính độ dài các cạnh chưa biết trong các tam giác sau:

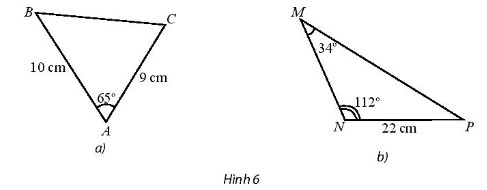
Lời giải:

a) Áp dụng định lí côsin ta có:

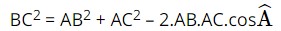
BC² = 10² + 9² – 2.10.9.cos65°

BC ² ≈ 104,929

BC ≈ 10,24 (cm).

Vậy BC ≈ 10,24 (cm).

Áp dụng định lí sin ta có:

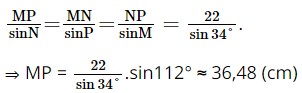
Vậy MP ≈ 36,48 cm, MN = 22 cm.

Bài 2 trang 74 SBT Toán 10 - Chân trời sáng tạo

Cho tam giác ABC , biết cạnh \(a = 75\) cm, \(\widehat B = 80^\circ ,\widehat C = 40^\circ \)

a) Tính các góc, các cạnh còn lại của tam giác ABC

b) Tính bán kính đường tròn ngoại tiếp của tam giác ABC

Lời giải:

Áp dụng định lí sin ta có:

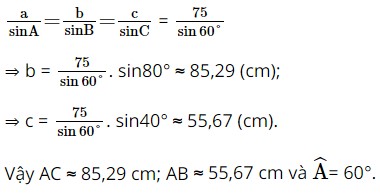
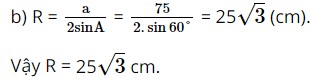
Bài 3 trang 75 SBT Toán 10 - Chân trời sáng tạo

Tính góc lớn nhất của tam giác ABC, biết các cạnh là \(a = 8,b = 12,c = 6\)

Lời giải:

Do b là cạnh lớn nhất nên B là góc lớn nhất.

Theo định lí côsin: b² = a² + c² – 2accosB

Bài 4 trang 75 SBT Toán 10 - Chân trời sáng tạo

Tính khoảng cách giữa hai điểm P và Q của một hồ nước (hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400 m và 600 m người quan sát nhìn thấy một góc \(76^\circ \)

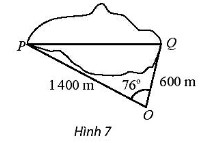
Lời giải:

Bài 5 trang 75 SBT Toán 10 - Chân trời sáng tạo

Cho tam giác ABC với \(BC = a;AC = b;AB = c\). Chứng minh rằng:

\(1 + \cos A = \frac{{\left( {a + b + c} \right)\left( { - a + b + c} \right)}}{{2bc}}\)

Lời giải:

Bài 6 trang 75 SBT Toán 10 - Chân trời sáng tạo

Cho tam giác ABC có \(a = 24\)cm, \(b = 26\)cm, \(c = 30\)cm

a) Tính diện tích tam giác ABC

b) Tính bán kính đường tròn nội tiếp của tam giác ABC

Lời giải:

Bài 7 trang 75 SBT Toán 10 - Chân trời sáng tạo

Cho tam giác MNP có \(MN = 10,MP = 20\) và \(\widehat M = 42^\circ \)

a) Tính diện tích tam giác MNP

b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP

Lời giải:

a) Diện tích tam giác MNP là:

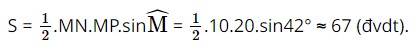
Vậy diện tích tam giác MNP là 67 đvdt.

b)

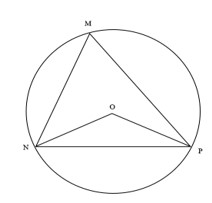
Áp dụng định lí côsin:

Xét đường tròn tâm O ngoại tiếp tam giác MNP:

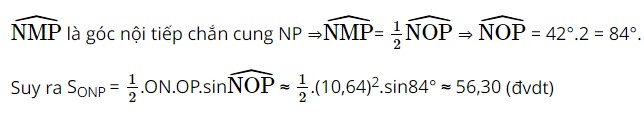
Vậy diện tích tam giác ONP là 56,30 đvdt.

Bài 8 trang 75 SBT Toán 10 - Chân trời sáng tạo

Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau

Lời giải:

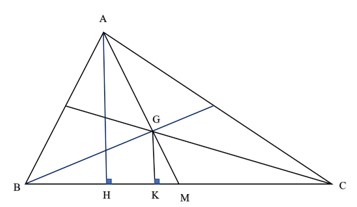
Vẽ AH và GK vuông góc với BC.

⇒ tam giác GKM và tam giác AHM đồng dạng (g.g).

Bài 9 trang 75 SBT Toán 10 - Chân trời sáng tạo

Cho tam giác ABC và có các điểm B’, C’ trên các cạnh AB, AC

Chứng minh  \(\frac{{{S_{ABC}}}}{{{S_{AB'C'}}}} = \frac{{AB.AC}}{{AB'.AC'}}\)

Lời giải:

Ta có:

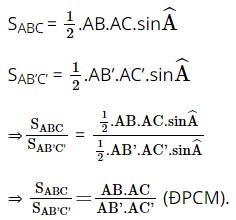
Bài 10 trang 75 SBT Toán 10 - Chân trời sáng tạo

Tính diện tích bề mặt của một miếng bánh mì kẹp kebab hình tam giác có hai cạnh lần lượt là 10 cm, 12 cm và góc tạo bởi hai cạnh đó là \(35^\circ \)

Lời giải:

Diện tích bề mặt miếng bánh mì kebab là:

Vậy diện tích bề mặt miếng bánh mì kebab khoảng 34,4 cm².

Sachbaitap.com