Giải SBT Toán 10 trang 73, 74 Cánh Diều tập 2

Bài 24 trang 73 SBT Toán 10 - Cánh Diều

Cho đường thẳng ∆: 2x − 3y + 5 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của ∆?

A.  \(\overrightarrow {{n_1}}  = (2; - 3)\)   B. \(\overrightarrow {{n_2}}  = ( - 3;2)\)                C. \(\overrightarrow {{n_3}}  = (2;3)\)                        D.  \(\overrightarrow {{n_4}}  = (3;2)\)

Lời giải:

∆: 2x − 3y + 5 = 0 có vectơ pháp tuyến là \(\overrightarrow n  = (2; - 3)\)   

Chọn A

Bài 25 trang 73 SBT Toán 10 - Cánh Diều

Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 - t\\y = 4 + 2t\end{array} \right.\). Vectơ nào dưới đây là một vectơ chỉ phương của ∆?

Lời giải:

\(\Delta :\left\{ \begin{array}{l}x = 3 - t\\y = 4 + 2t\end{array} \right.\) có một vectơ chỉ phương là \(\overrightarrow u  = ( - 1;2)\)    

Chọn C

Bài 26 trang 73 SBT Toán 10 - Cánh Diều

Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 - 5t\\y =  - 1 + 3t\end{array} \right.\). Trong các điểm có tọa độ dưới đây điểm nào nằm trên đường thẳng ∆?

A. (-3; -2)                    B. (2; -1)                     C. (-2; 1)                     D. (-5; 3)

Phương pháp:

Bước 1: Tìm điểm đi qua trên phương trình đường thẳng

Bước 2: Nếu không có điểm trên PT, thay tọa độ các điểm và giải tìm t, nếu 2 giá trị t trong hệ giống nhau thì điểm đó thuộc ∆

Lời giải:

Ta thấy điểm (2; -1) thuộc đường thẳng ∆     

Chọn B

Bài 27 trang 73 SBT Toán 10 - Cánh Diều

Cho đường thẳng ∆: x − 3y + 4 = 0. Phương trình nào dưới đây là phương trình tham số của ∆?

A. \(\left\{ \begin{array}{l}x =  - 1 + 3t\\y =  - 1 + t\end{array} \right.\)           B. \(\left\{ \begin{array}{l}x =  - 1 + 3t\\y = 1 + t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x =  - 1 - 3t\\y = 1 + t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 1 - t\end{array} \right.\)

Lời giải:

∆ có VTPT là \(\overrightarrow n  = (1; - 3) \Rightarrow \)VTCP của ∆ là \(\overrightarrow {{u_1}}  = (3;1)\)hoặc \(\overrightarrow {{u_2}}  = ( - 3; - 1)\) Loại C

Xét điểm (-1; 1) ta có -1 – 3.1 + 4 = 0 \( \Rightarrow ( - 1;1) \in \Delta \)

∆ có VTPT là \(\overrightarrow n  = (1; - 3) \Rightarrow \)VTCP của ∆ là \(\overrightarrow {{u_1}}  = (3;1)\)hoặc \(\overrightarrow {{u_2}}  = ( - 3; - 1)\) Loại C

Xét điểm (-1; 1) ta có -1 – 3.1 + 4 = 0 \( \Rightarrow ( - 1;1) \in \Delta \)

Chọn B

Bài 28 trang 73 SBT Toán 10 - Cánh Diều

Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x =  - 2 + 2t\\y = 3 - 5t\end{array} \right.\). Phương trình nào dưới đây là phương trình tổng quát của ∆?

A. 5x + 2y – 4 = 0       B. 2x - 5y + 19 = 0      C. -5x + 2y – 16 = 0    D. 5x + 2y + 4 = 0

Lời giải:

∆ có VTCP là \(\overrightarrow u  = (2; - 5) \Rightarrow \)VTPT của ∆ là \(\overrightarrow {{u_1}}  = (5;2)\)hoặc \(\overrightarrow {{u_2}}  = ( - 5; - 2)\) Loại B, C

∆ có điểm đi qua là (-2; 3)

PTTQ của ∆ là: 5x + 2y + 4 = 0    

Chọn D

Bài 29 trang 73 SBT Toán 10 - Cánh Diều

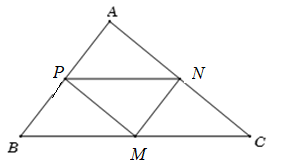
Cho tam giác ABC, biết toạ độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1 ; 1), N(3 ; 4), P(5 ; 6).

a) Viết phương trình tham số của các đường thẳng AB, BC, CA

b) Viết phương trình tổng quát của các đường trung trực của tam giác ABC

Lời giải:

a) Theo giả thiết, MN, MP, NP là các đường trung bình của ∆ABC \( \Rightarrow MN//AB,MP//AC,NP//BC\)

Khi đó, AB, AC, BC lần lượt nhận các vectơ \(\overrightarrow {MN}  = (4;3),\overrightarrow {MP}  = (6;5),\overrightarrow {NP}  = (2;2)\) làm VTCP

+ AB đi qua P, nhận \(\overrightarrow {MN}  = (4;3)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 5 + 4t\\y = 6 + 3t\end{array} \right.\)

+ AC đi qua N, nhận \(\overrightarrow {MP}  = (6;5)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 3 + 6k\\y = 4 + 5k\end{array} \right.\)

+ BC đi qua M, nhận \(\overrightarrow u  = (1;1)\)cùng phương với \(\overrightarrow {NP}  = (2;2)\) làm VTCP nên có PT tham số:

\(\left\{ \begin{array}{l}x =  - 1 + p\\y = 1 + p\end{array} \right.\)

b) Ta có:

+ Đường trung trực của cạnh AB đi qua P và nhận \(\overrightarrow {MN}  = (4;3)\) làm VTPT nên có PTTQ:

4x + 3y – 38 = 0

+ Đường trung trực của cạnh AC đi qua N và nhận \(\overrightarrow {MP}  = (6;5)\) làm VTPT nên có PTTQ:

6x + 5y – 38 = 0

+ Đường trung trực của cạnh BC đi qua M và nhận \(\overrightarrow {NP}  = (2;2)\) làm VTPT nên có PTTQ:

2x + 2y = 0 \( \Leftrightarrow x + y = 0\)

Bài 30 trang 73 SBT Toán 10 - Cánh Diều

Cho tam giác ABC có A(3 ; 7), B(–2 ; 2), C(6 ; 1). Viết phương trình tổng quát của các đường cao của tam giác ABC.

Lời giải:

Ta có: \(\overrightarrow {AB}  = ( - 5; - 5),\overrightarroaw {AC}  = (3; - 6),\overrightarrow {BC}  = (8; - 1)\)

Gọi AH, BM, CN là các đường cao của ∆ABC. Khi đó:

+ \(AH \bot BC \Rightarrow \) AH đi qua A và nhận \(\overrightarrow {BC}  = (8; - 1)\) làm VTPT nên có PT: 8x – y – 17 = 0

+ \(BM \bot AC \Rightarrow \) BM đi qua B và nhận \(\overrightarrow {{n_1}}  = (1; - 2)\) cùng phương với \(\overrightarrow {AC}  = (3; - 6)\) làm VTPT nên có PT:

x – 2y + 6 = 0

+ \(CN \bot AB \Rightarrow \) CN đi qua C và nhận \(\overrightarrow {{n_2}}  = (1;1)\) cùng phương với \(\overrightarrow {AB}  = ( - 5; - 5)\) làm VTPT nên có PT:

x + y – 7 = 0

Bài 31 trang 74 SBT Toán 10 - Cánh Diều

Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 4 + t\\y =  - 1 + 2t\end{array} \right.\) và điểm A(2 ; 1). Hai điểm M, N nằm trên ∆.

a) Tìm toạ độ điểm M sao cho AM = \(\sqrt {17} \)

b) Tìm toạ độ điểm N sao cho đoạn thẳng AN ngắn nhất

Lời giải:

Do \(M,N \in \Delta \) nên \(M(4 + t; - 1 + 2t)\) và \(N(4 + k; - 1 + 2k)\)

a) Ta có: \(\overrightarrow {AM}  = (t + 2;2t - 2)\)

Theo giả thiết, AM = \(\sqrt {17} \) \( \Rightarrow A{M^2} = 17 \Leftrightarrow {(t + 2)^2} + {(2t - 2)^2} = 17\)\( \Leftrightarrow 5{t^2} - 4t - 9 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\t = \frac{9}{5}\end{array} \right.\)

Với t = -1 thì \(M(3; - 3)\)

Với \(t = \frac{9}{5}\) thì \(M\left( {\frac{{29}}{5};\frac{{13}}{5}} \right)\)

Vậy có 2 điểm M thỏa mãn là \(M(3; - 3)\) và \(M\left( {\frac{{29}}{5};\frac{{13}}{5}} \right)\)

b) Ta có: \(\overrightarrow {AN}  = (k + 2;2k - 2)\)

\(AN = \sqrt {{{\left( {k + 2} \right)}^2} + {{(2k - 2)}^2}} \)\( \Leftrightarrow A{N^2} = {\left( {k + 2} \right)^2} + {(2k - 2)^2} \Leftrightarrow A{N^2} = 5{k^2} - 4k + 8\)

AN nhỏ nhất \( \Leftrightarrow A{N^2} = 5{k^2} - 4k + 8\) nhỏ nhất

Ta có: \(5{k^2} - 4k + 8 = 5{\left( {k - \frac{2}{5}} \right)^2} + \frac{{44}}{5}\)\( \Rightarrow A{N^2} \ge \frac{{44}}{5} \Rightarrow AN \ge \frac{{2\sqrt {55} }}{5}\)

Dấu “=” xảy ra khi và chỉ khi \(k = \frac{2}{5}\) \( \Rightarrow N\left( {\frac{{22}}{5}; - \frac{1}{5}} \right)\)

Bài 32 trang 74 SBT Toán 10 - Cánh Diều

Cho ba điểm A(-2 ; 2), B(7 ; 5), C(4 ; – 5) và đường thẳng ∆: 2x  + y – 4 = 0

a) Tìm toạ độ điểm M thuộc ∆ và cách đều hai điểm A và B

b*) Tìm toạ độ điểm N thuộc ∆ sao cho |\(\overrightarrow {NA}  + \overrightarrow {NB}  + \overrightarrow {NC} \)| có giá trị nhỏ nhất.

Lời giải:

a) Gọi \(M(t;4 - 2t) \in \Delta \)

Ta có: \(\overrightarrow {AM}  = (t + 2; - 2t + 2)\), \(\overrightarrow {BM}  = (t - 7; - 2t - 1)\)

Theo giả thiết, M cách đều hai điểm A và B \( \Rightarrow AM = BM \Leftrightarrow A{M^2} = B{M^2}\)

                                                            \( \Leftrightarrow {(t + 2)^2} + {( - 2t + 2)^2} = {(t - 7)^2} + {( - 2t - 1)^2}\)

                                                            \( \Leftrightarrow  - 4t + 8 =  - 10t + 50 \Leftrightarrow 6t = 42 \Leftrightarrow t = 7\)

Vậy M(7 ; -10)

b*) Ta có: \(\overrightarrow {AB}  = (9;3),\overrightarrow {AC}  = (6; - 7)\)

Vì \(\frac{9}{6} \ne \frac{3}{{ - 7}}\) nên \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương \( \Rightarrow A,B,C\) không thẳng hàng

Gọi G là trọng tâm ∆ABC \( \Rightarrow G\left( {3;\frac{2}{3}} \right)\) và \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Xét \(\left| {\overrightarrow {NA}  + \overrightarrow {NB}  + \overrightarrow {NC} } \right| = \left| {\overrightarrow {NG}  + \overrightarrow {GA}  + \overrightarrow {NG}  + \overrightarrow {GB}  + \overrightarrow {NG}  + \overrightarrow {GC} } \right|\)\( = \left| {3\overrightarrow {NG} } \right| = 3NG\)

\(\left| {\overrightarrow {NA}  + \overrightarrow {NB}  + \overrightarrow {NC} } \right|\) nhỏ nhất khi và chỉ khi NG nhỏ nhất \( \Leftrightarrow \) N là hình chiếu của G trên ∆

Gọi d là đường thẳng đi qua G, vuông góc với ∆

∆ có VTPT \(\overrightarrow n  = (2;1)\) \( \Rightarrow \) ∆ có một VTCP là \(\overrightarrow u  = (1; - 2)\)

Do \(d \bot \Delta \) nên d nhận \(\overrightarrow u  = (1; - 2)\)làm VTPT \( \Rightarrow \) d có PT: 3x – 6y – 5 = 0

N là giao điểm của d và ∆ \( \Rightarrow \) tọa độ điểm N là nghiệm của hệ PT: \(\left\{ \begin{array}{l}2x + y - 4 = 0\\3x - 6y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{29}}{{15}}\\y = \frac{2}{{15}}\end{array} \right.\)

Vậy \(N\left( {\frac{{29}}{{15}};\frac{2}{{15}}} \right)\)

Sachbaitap.com