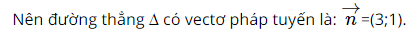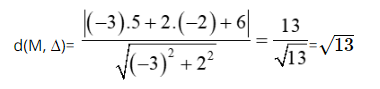Giải SBT Toán 10 trang 81, 82, 83 Cánh Diều tập 2

Bài 33 trang 81 SBT Toán 10 - Cánh Diều

Phương trình nào dưới đây là phương trình tham số của một đường thẳng song song với đường thẳng

x − 2y + 3 = 0?

A. \(\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 1 + t\end{array} \right.\)            B. \(\left\{ \begin{array}{l}x = 1 + 2t\\y =  - 1 + t\end{array} \right.\)                       C. \(\left\{ \begin{array}{l}x = 1 + t\\y =  - 1 - 2t\end{array} \right.\)          D. \(\left\{ \begin{array}{l}x = 1 - 2t\\y =  - 1 + t\end{array} \right.\)

Lời giải:

Đường thẳng ∆: x − 2y + 3 = 0 có VTPT là \(\overrightarrow n  = (1; - 2)\).

Đường thẳng d song song với ∆ nhận \(\overrightarrow n  = (1; - 2)\) làm VTPT và có VTCP là \(\overrightarrow u \) thỏa mãn \(\overrightarrow u .\overrightarrow n  = 0\)

 (Loại C, D)

Xét điểm M(-1; 1) thuộc đường thẳng \(\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 1 + t\end{array} \right.\). Ta thấy tọa độ M thỏa mãn PT x − 2y + 3 = 0 nên M nằm trên ∆ (Loại A)

 Chọn B

Bài 34 trang 81 SBT Toán 10 - Cánh Diều

Phương trình nào dưới đây là phương trình tham số của một đường thẳng vuông góc với đường thẳng

\(\left\{ \begin{array}{l}x =  - 1 + 3t\\y = 1 - 2t\end{array} \right.\)?

A. \(\left\{ \begin{array}{l}x =  - 1 - 2t\\y = 1 - 3t\end{array} \right.\)            B. \(\left\{ \begin{array}{l}x =  - 1 - 2t\\y = 1 + 3t\end{array} \right.\)           C. \(\left\{ \begin{array}{l}x =  - 1 - 3t\\y = 1 + 2t\end{array} \right.\)          D. \(\left\{ \begin{array}{l}x =  - 1 - 3t\\y = 1 - 2t\end{array} \right.\)

Lời giải:

Đường thẳng ∆: \(\left\{ \begin{array}{l}x =  - 1 + 3t\\y = 1 - 2t\end{array} \right.\) có VTCP \(\overrightarrow u  = (3; - 2)\)

Đường thẳng d vuông góc với ∆ có VTCP \(\overrightarrow v \) thỏa mãn \(\overrightarrow v .\overrightarrow u  = 0\)

Ta thấy vectơ \(\overrightarrow v  = ( - 2; - 3)\) thỏa mãn   

Chọn A

Bài 35 trang 81 SBT Toán 10 - Cánh Diều

Đường thẳng ∆ đi qua điểm M(−1 ; 2) và song song với đường thẳng d: 2x – y − 5 = 0 có phương trình tổng quát là:

A. 2x – y = 0               B. 2x – y + 4 = 0         C. 2x + y + 4 = 0         D. x + 2y – 3 = 0

Lời giải:

Vậy chọn đáp án B.

Bài 36 trang 81 SBT Toán 10 - Cánh Diều

Đường thẳng ∆ đi qua điểm M(3 ; -4) và vuông góc với đường thẳng  d: x − 3y + 1 = 0 có phương trình tổng quát là:

A. x - 3y – 15 = 0        B. -3x + y + 5 = 0        C. 3x + y – 13 = 0       D.  3x + y – 5 = 0

Phương pháp:

Bước 1: Tìm một VTPT của ∆ (thỏa mãn nhân vô hướng với VTPT của d bằng 0)

Bước 2: Viết PTTQ của ∆ biết điểm đi qua là M và VTPT đã tìm ở bước 1

Lời giải:

Đường thẳng ∆ vuông góc với đường thẳng d: x – 3y + 1 = 0

Đường thẳng ∆ đi qua M(3; - 4) nên có phương trình tổng quát là:

3(x - 3) + (y + 4) = 0 hay 3x + y - 5 = 0.

Vậy chọn đáp án D.

Bài 37 trang 81 SBT Toán 10 - Cánh Diều

Cho ∆₁: x − 2y + 3 = 0 và ∆₂: -2x – y + 5 = 0. Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰                          B. 45⁰                          C. 90°                          D. 60⁰

Lời giải:

Vậy 2 đường thẳng trên vuông góc với nhau, chọn đáp án C.

Bài 38 trang 82 SBT Toán 10 - Cánh Diều

Cho \({\Delta _1}:\left\{ \begin{array}{l}x =  - 2 + \sqrt 3 t\\y = 1 - t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x =  - 1 + \sqrt 3 t'\\y = 2 + t'\end{array} \right.\). Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰                          B. 45⁰                          C. 90⁰                          D. 60⁰

Lời giải:

∆₁ có VTCP là \(\overrightarrow {{u_1}}  = (\sqrt 3 ; - 1)\); ∆₂ có VTCP là \(\overrightarrow {{u_2}}  = (\sqrt 3 ;1)\)

Ta có: \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\sqrt 3 .\sqrt 3  + ( - 1).1}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{( - 1)}^2}} .\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {1^2}} }}\)\( = \frac{2}{4} = \frac{1}{2}\)\( \Rightarrow \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = {60^0}\)

  \( \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = {60^0}\)   

Chọn D

Bài 39 trang 82 SBT Toán 10 - Cánh Diều

Khoảng cách từ điểm M(5 ; – 2) đến đường thẳng ∆: - 3x + 2y + 6 = 0 là:

A. 13                           B. \(\sqrt {13} \)                     C. \(\frac{{\sqrt {13} }}{{13}}\)                        D. \(2\sqrt {13} \)

Lời giải:

Áp dụng công thức ta có:

Vậy chọn đáp án B.

Bài 40 trang 82 SBT Toán 10 - Cánh Diều

Xét vị trí tương đối của mỗi cặp đường thẳng sau:

a) \({d_1}:2x - 3y + 5 = 0\) và \({d_2}:2x + y - 1 = 0\)

b) \({d_3}:\left\{ \begin{array}{l}x =  - 1 - 3t\\y = 3 + t\end{array} \right.\) và \({d_4}:x + 3y - 5 = 0\)

c) \({d_5}:\left\{ \begin{array}{l}x = 2 - 2t\\y =  - 1 + t\end{array} \right.\) và \({d_6}:\left\{ \begin{array}{l}x =  - 2 + 2t'\\y = 1 - {t^'}\end{array} \right.\)

Lời giải:

a) \({d_1}:2x - 3y + 5 = 0\) và \({d_2}:2x + y - 1 = 0\)

Tọa độ giao điểm của d₁ và d₂ là nghiệm của hệ PT: \(\left\{ \begin{array}{l}2x - 3y + 5 = 0\\2x + y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 3y =  - 5\\2x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \frac{1}{4}\\y = \frac{3}{2}\end{array} \right.\)

Hệ trên có một nghiệm duy nhất. Vậy d₁ và d₂ cắt nhau.

b) \({d_3}:\left\{ \begin{array}{l}x =  - 1 - 3t\\y = 3 + t\end{array} \right.\) và \({d_4}:x + 3y - 5 = 0\)

d₃ đi qua điểm (-1; 3) và có VTCP là \(\overrightarrow u  = ( - 3;1)\) \( \Rightarrow \) d₃ có một VTPT là \(\overrightarrow {{n_1}}  = (1;3)\)

\( \Rightarrow \) d₃ và d₄ có cùng VTPT nên d₃ // d₄ hoặc d₃ và d₄ trùng nhau

Thay tọa độ điểm (-1; 3) vào PT d₄ ta có: -1 + 3.3 – 5 = 3 ≠ 0 \( \Rightarrow ( - 1;3) \notin {d_4}\)

Vậy d₃ // d₄

c) \({d_5}:\left\{ \begin{array}{l}x = 2 - 2t\\y =  - 1 + t\end{array} \right.\) và \({d_6}:\left\{ \begin{array}{l}x =  - 2 + 2t'\\y = 1 - t'\end{array} \right.\)

d₅ đi qua A(2; -1), có VTCP là \(\overrightarrow {{u_1}}  = ( - 2;1)\)

d₆ đi qua B(-2; 1), có VTCP là \(\overrightarrow {{u_2}}  = (2; - 1)\)

Ta thấy \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương nên d₅ // d₆ hoặc d₅ và d₆ trùng nhau

Thay tọa độ điểm A vào PT d6 ta có: \(\left\{ \begin{array}{l}2 =  - 2 + 2t'\\ - 1 = 1 - t'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t' = 2\\t' = 2\end{array} \right. \Leftrightarrow t' = 2 \Rightarrow A \in {d_6}\)

Vậy d₅ và d₆ trùng nhau

Bài 41 trang 82 SBT Toán 10 - Cánh Diều

Tìm số đo góc giữa hai đường thẳng của mỗi cặp đường thẳng sau:

a) ∆₁: 3x + y - 5 = 0 và ∆₂: x + 2y − 3 = 0

b) \({\Delta _3}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y =  - 1 + 3t\end{array} \right.\) và \({\Delta _4}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y =  - t'\end{array} \right.\)

c) \({\Delta _5}: - \sqrt 3 x + 3y + 2 = 0\) và \({\Delta _6}:\left\{ \begin{array}{l}x = 3t\\y = 1 - \sqrt 3 t\end{array} \right.\)

Lời giải:

a) ∆₁: 3x + y - 5 = 0 và ∆₂: x + 2y − 3 = 0

∆₁ có VTPT là \(\overrightarrow {{n_1}}  = (3;1)\); ∆₂ có VTPT là \(\overrightarrow {{n_2}}  = (1;2)\)

Ta có: \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{3.1 + 1.2}}{{\sqrt {{3^2} + {1^2}} .\sqrt {{1^2} + {2^2}} }}\)\( = \frac{{\sqrt 2 }}{2}\)\( \Rightarrow \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = {45^0}\)

Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^0}\)

b) \({\Delta _3}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y =  - 1 + 3t\end{array} \right.\) và \({\Delta _4}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y =  - t'\end{array} \right.\)

∆₃ có VTCP là \(\overrightarrow {{u_1}}  = (\sqrt 3 ;3)\); ∆₄ có VTPT là \(\overrightarrow {{u_2}}  = ( - \sqrt 3 ; - 1)\)

Ta có: \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\sqrt 3 .\left( { - \sqrt 3 } \right) + 3.( - 1)}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {3^2}} .\sqrt {{{\left( { - \sqrt 3 } \right)}^2} + {{( - 1)}^2}} }}\)\( =  - \frac{{\sqrt 3 }}{2}\)\( \Rightarrow \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = {150^0}\)

Vậy \(\left( {{\Delta _3},{\Delta _4}} \right) = {180^0} - {150^0} = {30^0}\)

c) \({\Delta _5}: - \sqrt 3 x + 3y + 2 = 0\) và \({\Delta _6}:\left\{ \begin{array}{l}x = 3t\\y = 1 - \sqrt 3 t\end{array} \right.\)

∆₅ có VTPT là \(\overrightarrow n  = ( - \sqrt 3 ;3)\) \( \Rightarrow {\Delta _5}\) có một VTCP là \(\overrightarrow {{u_3}}  = (3;\sqrt 3 )\)

∆₆ có VTCP là \(\overrightarrow {{u_4}}  = (3; - \sqrt 3 )\)

Ta có: \(\cos \left( {\overrightarrow {{u_3}} ,\overrightarrow {{u_4}} } \right) = \frac{{3.3 + \sqrt 3 .\left( { - \sqrt 3 } \right)}}{{\sqrt {{3^2} + {{\left( {\sqrt 3 } \right)}^2}} .\sqrt {{3^2} + {{\left( { - \sqrt 3 } \right)}^2}} }}\)\( = \frac{1}{2}\)\( \Rightarrow \left( {\overrightarrow {{u_3}} ,\overrightarrow {{u_4}} } \right) = {60^0}\)

Vậy \(\left( {{\Delta _5},{\Delta _6}} \right) = {60^0}\)

Bài 42 trang 82 SBT Toán 10 - Cánh Diều

Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau:

a) A(−3 ; 1) và ∆₁: 2x + y - 4 = 0

b) B(1; -3) và ∆₂: \(\left\{ \begin{array}{l}x =  - 3 + 3t\\y = 1 - t\end{array} \right.\)

Lời giải:

a) Ta có: \(d(A,{\Delta _1}) = \frac{{\left| {2.( - 3) + 1 - 4} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{{\left| { - 9} \right|}}{{\sqrt 5 }} = \frac{{9\sqrt 5 }}{5}\)

b) ∆₂ đi qua điểm (-3; 1) và có VTCP là \(\overrightarrow u  = (3; - 1)\) \( \Rightarrow {\Delta _2}\) có một VTPT là \(\overrightarrow n  = (1;3)\)

∆₂ có PTTQ: x + 3y = 0

Ta có: \(d(B,{\Delta _2}) = \frac{{\left| {1.1 + 3.( - 3)} \right|}}{{\sqrt {{1^2} + {3^2}} }} = \frac{{\left| { - 8} \right|}}{{\sqrt {10} }} = \frac{{4\sqrt {10} }}{5}\)

 Bài 43 trang 82 SBT Toán 10 - Cánh Diều

Cho hai đường thẳng song song ∆₁: ax + by + c = 0 và ∆₂: ax + by + d = 0. Chứng minh rằng khoảng cách giữa hai đường thẳng ∆₁ và ∆₂  bằng \(\frac{{\left| {d - c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Lời giải:

Gọi \(M\left( {{x_M};\frac{{ - c - a{x_M}}}{b}} \right)\) thuộc đường thẳng ∆₁

Do ∆₁ // ∆₂  nên \(d({\Delta _1},{\Delta _2}) = d(M,{\Delta _2})\)

Ta có: \(d(M,{\Delta _2}) = \frac{{\left| {a.{x_M} + b.\frac{{ - c - a{x_M}}}{b} + d} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)\( = \frac{{\left| {a{x_M} - c - a{x_M} + d} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {d - c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Vậy \(d({\Delta _1},{\Delta _2}) = \frac{{\left| {d - c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) (ĐPCM)

Bài 44 trang 82 SBT Toán 10 - Cánh Diều

Cho hai đường thẳng ∆₁: mx – 2y – 1 = 0 và ∆₂: x - 2y + 3 = 0. Với giá trị nào của tham số m thì:

a) ∆₁ // ∆₂?

b) ∆₁\( \bot {\Delta _2}\)?

Lời giải:

∆₁ có VTPT là \(\overrightarrow {{n_1}}  = (m; - 2)\); ∆₂ có VTPT là \(\overrightarrow {{n_2}}  = (1; - 2)\)

a) ∆₁ // ∆₂ khi và chỉ khi \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cùng phương và ∆₁ và ∆₂ không trùng nhau

\( \Leftrightarrow \frac{m}{1} = \frac{{ - 2}}{{ - 2}} \ne \frac{{ - 1}}{3} \Leftrightarrow m = 1\)

Vậy với m = 1 thì ∆₁ // ∆₂

b) \({\Delta _1} \bot {\Delta _2} \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0 \Leftrightarrow m + 4 = 0 \Leftrightarrow m =  - 4\)

Vậy với m = -4 thì \({\Delta _1} \bot {\Delta _2}\)

Bài 45 trang 82 SBT Toán 10 - Cánh Diều

Cho ba điểm A(-2; 2), B(4 ; 2), C(6 ; 4). Viết phương trình đường thẳng ∆ đi qua B đồng thời cách đều A và C.

Phương pháp:

Gọi đường thẳng ∆ có dạng: ax + by + c = 0 (1)

Bước 1: Thay tọa độ B vào PT (1) rồi biểu diễn c theo a và b

Bước 2: Sử dụng công thức khoảng cách để lập PT dạng d(A, ∆) = d(C, ∆)

Bước 3: Giải PT trên tìm mối liên hệ giữa a và b

Bước 4: Lựa chọn 2 giá trị a và b theo mối liên hệ rồi viết PT ∆

Lời giải:

Giả sử ∆ có dạng: ax + by + c = 0 (1)

Do \(B(4;2) \in \Delta \) nên \(4a + 2b + c = 0 \Rightarrow c =  - 4a - 2b\)\( \Rightarrow \Delta :ax + by - 4a - 2b = 0\)

Theo giả thiết, d(A, ∆) = d(C, ∆) \( \Leftrightarrow \frac{{\left| { - 2a + 2b - 4a - 2b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {6a + 4b - 4a - 2b} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

                                                 \( \Rightarrow \left| { - 6a} \right| = \left| {2a + 2b} \right| \Leftrightarrow 6\left| a \right| = \left| {2a + 2b} \right| \Leftrightarrow \left[ \begin{array}{l}6a = 2a + 2b\\6a =  - 2a - 2b\end{array} \right.\)

                                                 \( \Leftrightarrow \left[ \begin{array}{l}4a = 2b\\8a =  - 2b\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2a = b\\ - 4a = b\end{array} \right.\)

+ Với 2a = b, chọn \(a = 1 \Rightarrow b = 2\)\( \Rightarrow \) ∆ có PT: x + 2y – 8 = 0

+ Với -4a = b, chọn \(a = 1 \Rightarrow b =  - 4\)\( \Rightarrow \) ∆ có PT: x – 4y + 4 = 0

Vậy có 2 đường thẳng ∆ thỏa mãn là x + 2y – 8 = 0 và x – 4y + 4 = 0

Bài 46 trang 83 SBT Toán 10 - Cánh Diều

Có hai tàu điện ngầm A và B chạy trong nội đô thành phố củng xuất phát tử hai ga, chuyển động đều theo đường thẳng. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng toạ độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), sau khi xuất phát t (giờ) (t ≥ 0), vị trí của tàu A có toạ độ được xác định bởi công thức: \(\left\{ \begin{array}{l}x = 7 + 36t\\y =  - 8 + 8t\end{array} \right.\) , vị trí của tàu B có toạ độ là (9 + 8t ; 5 – 36t).

a) Tính côsin góc giữa hai đường đi của hai tàu A và B

b) Sau bao lâu kể từ thời điểm xuất phát hai tàu gần nhau nhất?

Lời giải:

a) Tàu A chuyển động theo chiều vectơ \(\overrightarrow {{u_1}}  = (36;8)\); tàu B chuyển động theo chiều vectơ \(\overrightarrow {{u_2}}  = (8; - 36)\)

Ta có: \(\overrightarrow {{u_1}} .\overrightarrow {{u_2}}  = 36.8 + 8.( - 36) = 0\)\( \Rightarrow \overrightarrow {{u_1}}  \bot \overrightarrow {{u_2}}  \Rightarrow \cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = 0\)

Gọi \(\alpha \) là góc giữa hai đường đi của hai tàu. Khi đó \(\cos \alpha  = \left| {\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right| = 0\)

b) Sau t giờ: tàu A ở vị trí điểm \(M(7 + 36t; - 8 + 8t)\); tàu B ở vị trí điểm \(N(9 + 8t;5 - 36t)\)

Ta có: \(\overrightarrow {MN}  = ( - 28t + 2; - 44t + 13) \Rightarrow MN = \sqrt {{{( - 28t + 2)}^2} + {{( - 44t + 13)}^2}} \)

                                               \( \Leftrightarrow M{N^2} = {( - 28t + 2)^2} + {( - 44t + 13)^2} = 2720{t^2} - 1256t + 173\)

Theo giả thiết, MN đạt GTNN \( \Leftrightarrow M{N^2}\) đạt GTNN

Xét \(M{N^2} = 2720{t^2} - 1256t + 173 = 2720{\left( {t - \frac{{157}}{{680}}} \right)^2} + \frac{{4761}}{{170}}\)\( \ge \frac{{4761}}{{170}}\) \( \Rightarrow MN \ge \sqrt {\frac{{4761}}{{170}}} \)

Dấu “=” xảy ra khi và chỉ khi t = \(\frac{{157}}{{680}}\)

Vậy sau \(\frac{{157}}{{680}}\) giờ thì hai tàu gần nhau nhất và cách nhau một khoảng là 5,29 km

Sachbaitap.com