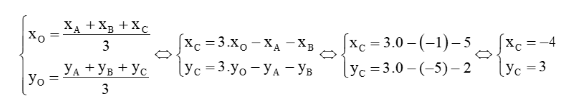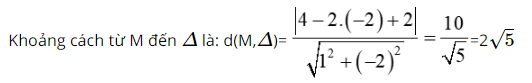Giải SBT Toán 10 trang 97-98-99 Cánh Diều tập 2

Bài 71 trang 97 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho A(–2 ; 1), B(1 ; –3). Toạ độ của vectơ \(\overrightarrow {AB} \) là:

A. (1 ; -4)                    B. (-3 ; 4)                    C. (3 ; -4)                    D. (1 ; -2)

Phương pháp:

Nếu \(A({x_A};{y_A}),B({x_B};{y_B})\) thì \(\overrightarrow {AB}  = ({x_B} - {x_A};{y_B} - {y_A})\)

Lời giải:

Vậy chọn đáp án C.

Bài 72 trang 97 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(− 1 ; − 5), B(5 ; 2) và trọng tâm là gốc toạ độ. Toạ độ điểm C là:

A. (4 ; -3)                    B. (-4 ; -3)                   C. (-4 ; 3)                    D. (4 ; 3)

Phương pháp:

Áp dụng kết quả: Nếu G(a; b) là trọng tâm của ∆ABC với \(A({x_A};{y_A}),B({x_B};{y_B}),C({x_C};{y_C})\) thì \(\left\{ \begin{array}{l}a = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\b = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\) để tìm tọa độ điểm C 

Lời giải:

Do trọng tâm tam giác là gốc tọa độ nên ta có:

Suy ra tọa độ C(– 4; 3).

Vậy chọn đáp án C

Bài 73 trang 97 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, vectơ nào sau đây có độ dài bằng 1?

A. \(\overrightarrow a  = (1;1)\)                  B. \(\overrightarrow b  = \left( {\frac{1}{2}; - \frac{1}{2}} \right)\)             C. \(\overrightarrow c  = \left( {\frac{1}{{\sqrt 3 }};\frac{2}{3}} \right)\)                       D. \(\overrightarrow d  = \left( {\frac{1}{{\sqrt 2 }}; - \frac{{\sqrt 2 }}{2}} \right)\)

Lời giải:

Ta có: \(\left| {\overrightarrow d } \right| = \sqrt {{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2} + {{\left( { - \frac{{\sqrt 2 }}{2}} \right)}^2}}  = 1\)   

Chọn D

Bài 74 trang 98 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, đường thẳng ∆ đi qua điểm M(–2 ; 0) và song song với đường thẳng

d: 2x - y + 2 = 0 có phương trình là:

A. 2x – y = 0               B. 2x – y + 4 = 0         C. 2x + y + 4 = 0         D. x + 2y + 2 = 0

Phương pháp:

Bước 1: Tìm VTPT của ∆ (là VTPT của d)

Bước 2: Viết PT đường thẳng ∆ đi qua M và có VTPT tìm được ở bước 1

Lời giải:

Đường thẳng ∆ song song với đường thẳng d: 2x – y + 2 = 0

Nên ∆ có dạng 2x – y + c = 0

M(-2; 0) thuộc ∆ nên 2. (-2) – 0 + c = 0 $\iff$c=4

Suy ra đường thẳng ∆ là: 2x – y + 4 = 0.

Vậy chọn đáp án B.

Bài 75 trang 98 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y =  - 1 + 3t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y =  - t'\end{array} \right.\)

Số đo góc giữa hai đường thẳnag ∆₁ và ∆₂ là:

A. 30⁰                          B. 45⁰                          C. 90⁰                          D. 60⁰ 

Lời giải:

∆₁ có VTCP là \(\overrightarrow u  = (\sqrt 3 ;3)\) ; ∆₂ có VTCP là \(\overrightarrow v  = ( - \sqrt 3 ; - 1)\)

Ta có: \(\left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\sqrt 3 .\left( { - \sqrt 3 } \right) + 3.( - 1)}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {3^2}} .\sqrt {{{\left( { - \sqrt 3 } \right)}^2} + {{( - 1)}^2}} }}\)\( =  - \frac{{\sqrt 3 }}{2}\)\( \Rightarrow \left( {\overrightarrow u ,\overrightarrow v } \right) = {150^0}\)

Vậy góc giữa ∆₁ và ∆₂ bằng 30⁰    

Chọn A

Bài 76 trang 98 SBT Toán 10 - Cánh Diều

Khoảng cách từ điểm M(4 ; –2) đến đường thẳng ∆: x − 2y + 2 = 0 bằng:

A. \(\frac{{2\sqrt 5 }}{5}\)                 B. \(2\sqrt 5 \)            C. 2.                D. \(\sqrt 5 \)

Phương pháp:

Áp dụng công thức tính khoảng cách từ một điểm \(M({x_M};{y_M})\) đến đường thẳng \(\Delta :ax + by + c = 0\):

\(d(M,\Delta ) = \frac{{\left| {a{x_M} + b{y_M} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Lời giải:

Vậy chọn đáp án B.

Bài 77 trang 98 SBT Toán 10 - Cánh Diều

Phương trình nào dưới đây là phương trình đường tròn?

A. (x + 3)² - (y + 4)² = 100                              B. (x + 3)² + (y + 4)² = 100

C. 2(x + 3)² + (y + 4)² = 100                           D. (x + 3)² + 2(y + 4)² = 100

Phương pháp:

PT đường tròn có dạng \({(x - a)^2} + {(y - b)^2} = c\)

Lời giải:

Ta thấy PT (x + 3)² + (y + 4)² = 100 là PT đường tròn dạng chính tắc   

Chọn B

Bài 78 trang 98 SBT Toán 10 - Cánh Diều

Phương trình nào dưới đây là phương trình chính tắc của đường hypebol?

A. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)            B. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{16}^2}}} =  - 1\) C. \(\frac{{{x^2}}}{{{{16}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)    D. \(\frac{{{x^2}}}{{{{15}^2}}} - \frac{{{y^2}}}{{{{16}^2}}} = 1\)

Lời giải:

Xét đáp án D ta có: PT \(\frac{{{x^2}}}{{{{15}^2}}} - \frac{{{y^2}}}{{{{16}^2}}} = 1\) có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với a = \(15\), b = 16 nên là PT hypebol

Chọn D

Bài 79 trang 98 SBT Toán 10 - Cánh Diều

Phương trình nào dưới đây là phương trình chính tắc của đường parabol?

A. \({y^2} = \frac{x}{{10}}\)             B. \({y^2} = \frac{{ - x}}{{10}}\)                        C. \({x^2} = \frac{y}{{10}}\)              D. \({x^2} = \frac{{ - y}}{{10}}\)

Lời giải:

Xét đáp án A ta có: PT \({y^2} = \frac{x}{{10}}\) có dạng \({y^2} = 2px\) với \(p = \frac{1}{{20}} > 0\) nên là PT hypebol

Chọn A

Bài 80 trang 99 SBT Toán 10 - Cánh Diều

Đường elip \(\frac{{{x^2}}}{{40}} + \frac{{{y^2}}}{{36}} = 1\) có hai tiêu điểm là:

A. F₁(-2 ; 0),  F₂ (2 ; 0)                                   B. F₁(-4 ; 0),  F₂(4 ; 0)

C. F₁(0 ; -2),  F₂(0 ; 2)                                    D. F₁(0 ; -4),  F₂ (0 ; 4)

Lời giải:

Theo giả thiết, elip có PT \(\frac{{{x^2}}}{{40}} + \frac{{{y^2}}}{{36}} = 1\) \( \Rightarrow {a^2} = 40,{b^2} = 36 \Rightarrow {c^2} = {a^2} - {b^2} = 4\)

Vậy elip có 2 tiêu điểm là F₁(-2 ; 0),  F₂ (2 ; 0)   

Chọn A

Bài 81 trang 99 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(-3 ; -1), B(3 ; 5), C(3 ; -4). Gọi G, H, I lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC.

a) Lập phương trình các đường thẳng AB, BC, AC

b) Tìm toạ độ các điểm G, H, I

c) Tính diện tích tam giác ABC

Phương pháp:

a) Tìm các VTPT của các đường thẳng AB, BC, AC rồi viết PTTQ

b) Tham số hóa tọa độ các điểm G, H, I (nếu cần)

 Bước 1: Tìm tọa độ trọng tâm G theo công thức \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\)

Bước 2: Giải hệ PT: \(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\\overrightarrow {BH} .\overrightarrow {AC}  = 0\end{array} \right.\) để tìm tọa độ trực tâm H

Bước 3: Giải hệ PT: \(\left\{ \begin{array}{l}IA = IB\\IA = IC\end{array} \right.\) để tìm tọa độ tâm I

Bước 4: Tính khoảng cách từ A đến BC là chiều cao của ∆ABC

Bước 5: Tính độ dài BC rồi tính diện tích ∆ABC

Lời giải:

a) Ta có: \(\overrightarrow {AB}  = (6;6),\overrightarrow {BC}  = (0; - 9),\overrightarrow {AC}  = (6; - 3)\)

+ Chọn \(\overrightarrow {{n_1}}  = (1; - 1)\) thỏa mãn \(\overrightarrow {{n_1}} .\overrightarrow {AB}  = 0\). Khi đó AB đi qua A(-3 ; -1) và nhận \(\overrightarrow {{n_1}}  = (1; - 1)\) nên có PT:

x - y + 2 = 0

+ Chọn \(\overrightarrow {{n_2}}  = (1;0)\) thỏa mãn \(\overrightarrow {{n_2}} .\overrightarrow {BC}  = 0\). Khi đó BC đi qua B(3 ; 5) và nhận \(\overrightarrow {{n_2}}  = (1;0)\) nên có PT: x – 3 = 0

+ Chọn \(\overrightarrow {{n_3}}  = (1;2)\) thỏa mãn \(\overrightarrow {{n_3}} .\overrightarrow {AC}  = 0\). Khi đó AC đi qua C(3 ; -4) và nhận \(\overrightarrow {{n_3}}  = (1;2)\) nên có PT:

x + 2y + 5 = 0

b) Ta có:

+ G là trọng tâm ∆ABC nên \( \Rightarrow G(1;0)\)

+ Gọi \(H({x_H};{y_H})\) là trực tâm ∆ABC . Ta có: \(\overrightarrow {AH}  = ({x_H} + 3;{y_H} + 1),\overrightarrow {BH}  = ({x_H} - 3;{y_H} - 5)\)

Khi đó\(\left\{ \begin{array}{l}AH \bot BC\\BH \bot AC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\\overrightarrow {BH} .\overrightarrow {AC}  = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - 9({y_H} + 1) = 0\\6({x_H} - 3) - 3({y_H} - 5)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_H} + 1 = 0\\2{x_H} - {y_H} - 1 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} =  - 1\end{array} \right.\)

\( \Rightarrow H(0; - 1)\)

+ Gọi \(I({x_I};{y_I})\) là tâm đường tròn ngoại tiếp tam giác ABC

Ta có: \(\overrightarrow {IA}  = {( - 3 - {x_I}; - 1 - {y_I})^2} \Rightarrow IA = \sqrt {{{({x_I} + 3)}^2} + {{({y_I} + 1)}^2}}  \Rightarrow I{A^2} = {({x_I} + 3)^2} + {({y_I} + 1)^2}\)

          \(\overrightarrow {IB}  = {(3 - {x_I};5 - {y_I})^2} \Rightarrow IB = \sqrt {{{({x_I} - 3)}^2} + {{({y_I} - 5)}^2}}  \Rightarrow I{B^2} = {({x_I} - 3)^2} + {({y_I} - 5)^2}\)

          \(\overrightarrow {IC}  = {(3 - {x_I}; - 4 - {y_I})^2} \Rightarrow IC = \sqrt {{{({x_I} - 3)}^2} + {{({y_I} + 4)}^2}}  \Rightarrow I{C^2} = {({x_I} - 3)^2} + {({y_I} + 4)^2}\)

Khi đó \(\left\{ \begin{array}{l}IA = IB\\IA = IC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}I{A^2} = I{B^2}\\I{A^2} = I{C^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{({x_I} + 3)^2} + {({y_I} + 1)^2} = {({x_I} - 3)^2} + {({y_I} - 5)^2}\\{({x_I} + 3)^2} + {({y_I} + 1)^2} = {({x_I} - 3)^2} + {({y_I} + 4)^2}\end{array} \right.\)

                         \( \Leftrightarrow \left\{ \begin{array}{l}12{x_I} + 12{y_I} = 24\\12{x_I} - 6{y_I} = 15\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} + {y_I} = 2\\4{x_I} - 2{y_I} = 5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \frac{3}{2}\\{y_I} = \frac{1}{2}\end{array} \right.\)\( \Rightarrow I\left( {\frac{3}{2};\frac{1}{2}} \right)\)

Vậy \(G(1;0),H(0; - 1),I\left( {\frac{3}{2};\frac{1}{2}} \right)\)

c) Ta có: \(d(A,BC) = \frac{{\left| { - 3 - 3} \right|}}{1} = 6\)

\(\overrightarrow {BC}  = (0; - 9) \Rightarrow BC = 9\)

Diện tích tam giác ABC là: \(S = \frac{1}{2}AD.BC = \frac{1}{2}.6.9 = 27\)

Bài 82 trang 99 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho hai điểm F₁(−4 ; 0) và F₂(4 ; 0).

a) Lập phương trình đường tròn có đường kính là F₁F₂

b) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn MF₁ + MF₂ = 12 là một đường conic (E). Cho biết (E) là đường conic nào và viết phương trình chính tắc của (E)

c) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn |MF₁ – MF₂| = 4 là một đường conic (H). Cho biết (H) là đường conic nào và viết phương trình chính tắc của (H)

Lời giải:

a) Gọi I là trung điểm của F₁F₂ \( \Rightarrow I(0;0)\)\( \Rightarrow I{F_1} = I{F_2} = 4\)

Đường tròn đường kính F₁F₂ có tâm I(0 ; 0) và bán kính R = 4 có PT: \({x^2} + {y^2} = 16\)

b) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn MF₁ + MF₂ = 12 là đường elip (E)

Ta có: MF₁ + MF₂ = 12 = 2a \( \Rightarrow a = 6\)

         \({F_1}{F_2} = 8 = 2c \Rightarrow c = 4\)

Khi đó \({b^2} = {a^2} - {c^2} = 36 - 16 = 20\)

Vậy elip (E) có PT: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{20}} = 1\)

b) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn |MF₁ – MF₂| = 4 là đường hypebol (H)

Ta có: |MF₁ – MF₂| = 4 = 2a \( \Rightarrow a = 2\)

         \({F_1}{F_2} = 8 = 2c \Rightarrow c = 4\)

Khi đó \({b^2} = {c^2} - {a^2} = 16 - 4 = 12\)

Vậy hypebol (H) có PT: \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{{12}} = 1\)

Bài 83 trang 99 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(−1 ; −2), đường trung tuyến kẻ từ B và đường cao kẻ từ C lần lượt có phương trình là 5x + y – 9 = 0 và x + 3y − 5 = 0. Tìm toạ độ của hai điểm B và C.

Lời giải:

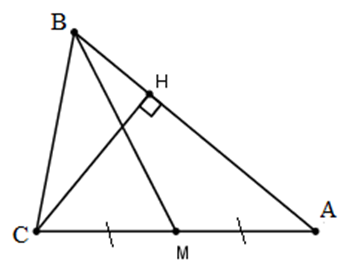
Gọi BM là đường trung tuyến kẻ từ B \( \Rightarrow BM\) có PT: 5x + y – 9 = 0

Gọi CH là đường cao kẻ từ C \( \Rightarrow CH\) có PT: x + 3y − 5 = 0

CH có VTPT \(\overrightarrow {{n_1}}  = (1;3)\) \( \Rightarrow CH\) có VTCP \(\overrightarrow {{u_1}}  = (3; - 1)\)

Ta có: \(CH \bot AB\) \( \Rightarrow AB\) đi qua A(−1 ; −2) và nhận \(\overrightarrow {{u_1}}  = (3; - 1)\) làm VTPT nên có PT:

3x – y + 1 = 0

Do B là giao điểm của BM và AB nên tọa độ điểm B là nghiệm của hệ PT:

\(\left\{ \begin{array}{l}5x + y - 9 = 0\\3x - y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right. \Rightarrow B(1;4)\)

Do \(M \in BM\) nên \(M(t;9 - 5t)\)

Theo giả thiết, M là trung điểm AC \( \Rightarrow C(2t + 1; - 10t + 20)\)

Do \(C \in CH\) nên \(2t + 1 + 3( - 10t + 20) - 5 = 0 \Leftrightarrow  - 28t + 56 = 0 \Leftrightarrow t = 2\) \( \Leftrightarrow C(5;0)\)

Vậy \(B(1;4)\) và \(C(5;0)\)

Bài 84 trang 99 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho hai điểm A(1 ; 0) và B(0 ; 3). Tìm tập hợp các điểm M thỏa mãn MA = 2MB.

Lời giải:

Gọi M(x ; y)

Ta có: \(\overrightarrow {AM}  = (a - 1;b) \Rightarrow AM = \sqrt {{{(x - 1)}^2} + {y^2}}  \Rightarrow A{M^2} = {(x - 1)^2} + {y^2}\)

         \(\overrightarrow {BM}  = (a;b - 3) \Rightarrow BM = \sqrt {{x^2} + {{(y - 3)}^2}}  \Rightarrow B{M^2} = {x^2} + {(y - 3)^2}\)

Theo giả thiết, \(MA = 2MB \Rightarrow M{A^2} = 4M{B^2}\) \( \Leftrightarrow {(x - 1)^2} + {y^2} = 4\left[ {{x^2} + {{(y - 3)}^2}} \right]\)

                                           \( \Leftrightarrow 3{x^2} + 3{y^2} + 2x - 24y + 35 = 0\)\( \Leftrightarrow {x^2} + {y^2} + \frac{2}{3}x - 8y + \frac{{35}}{3} = 0\)

                                     \( \Leftrightarrow {\left( {x + \frac{1}{3}} \right)^2} + {\left( {y - 4} \right)^2} = \frac{{40}}{9}\)

Vậy tập hợp các điểm M thỏa mãn MA = 2MB  là đường tròn có PT: \({\left( {x + \frac{1}{3}} \right)^2} + {\left( {y - 4} \right)^2} = \frac{{40}}{9}\) với tâm là \(I\left( { - \frac{1}{3};4} \right)\) và bán kính \(R = \frac{{2\sqrt {10} }}{3}\).

Sachbaitap.com