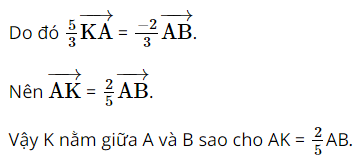Giải SBT Toán 10 trang 96, 97 Chân trời sáng tạo tập 1

Bài 1 trang 96 SBT Toán 10 - Chân trời sáng tạo

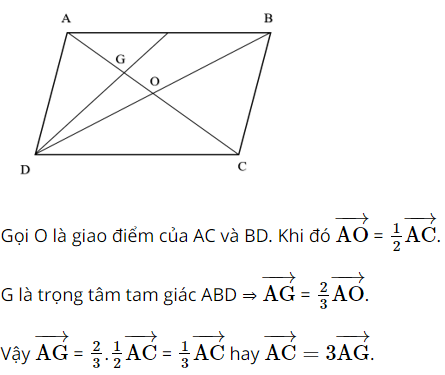
Cho hình bình hành ABCD có G là trọng tâm của tam giác ABD.

Chứng minh rằng: \(\overrightarrow {AC}  = 3\overrightarrow {AG} \)

Lời giải:

Bài 2 trang 97 SBT Toán 10 - Chân trời sáng tạo

Gọi AM  là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng:

a) \(2\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = \overrightarrow 0 \)

b)  \(2\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 4\overrightarrow {OD} \)        với O là điểm tùy ý

Phương pháp:

Sử dụng tính chất trung điểm \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \) với I là trung điểm của AB

Lời giải:

a) AM  là trung tuyến của tam giác ABC, suy ra M là trung điểm của BC

\(2\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DA}  + \left( {\overrightarrow {DB}  + \overrightarrow {DC} } \right) \\= 2\overrightarrow {DA}  + 2\overrightarrow {DM}  = 2\left( {\overrightarrow {DA}  + \overrightarrow {DM} } \right) = \overrightarrow 0 \)

(D là trung điểm của AM nên \(\overrightarrow {DA}  + \overrightarrow {DM}  = \overrightarrow 0 \))

b)

\(\begin{array}{l}2\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 2\overrightarrow {OA}  + \left( {\overrightarrow {OB}  + \overrightarrow {OC} } \right) = 2\overrightarrow {OA}  + 2\overrightarrow {OM} \\ = 2\left( {\overrightarrow {OA}  + \overrightarrow {OM} } \right) = 2.2\overrightarrow {OD}  = 4\overrightarrow {OD} \end{array}\)

Bài 3 trang 97 SBT Toán 10 - Chân trời sáng tạo

Lấy một điểm M tùy ý. Chứng minh rằng:

a) I là trung điểm của đoạn thẳng AB khi và chỉ khi \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \)

b) G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MG} \)

Lời giải:

Bài 4 trang 97 SBT Toán 10 - Chân trời sáng tạo

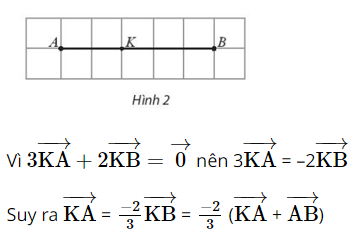
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho \(3\overrightarrow {KA}  + 2\overrightarrow {KB}  = \overrightarrow 0 \).

Lời giải:

Bài 5 trang 97 SBT Toán 10 - Chân trời sáng tạo

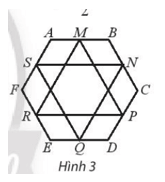
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Lời giải:

Gọi O là trọng tâm của tam giác MPR

Ta có MN là đường trung bình của tam giác ABC nên \(\overrightarrow {MN}  = \frac{1}{2}\overrightarrow {AC} \)

Tương tự PQ và RS cũng là đường trung bình của tam giác CDE và EFA nên

\(\overrightarrow {PQ}  = \frac{1}{2}\overrightarrow {CE} ;\overrightarrow {RS}  = \frac{1}{2}\overrightarrow {EA} \)

Từ đó suy ra \(\overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RS}  = \frac{1}{2}\overrightarrow {AC}  + \frac{1}{2}\overrightarrow {CE}  + \frac{1}{2}\overrightarrow {EA}  = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {CE}  + \overrightarrow {EA} } \right) = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RS}  = \overrightarrow 0 \)

\( \Leftrightarrow \left( {\overrightarrow {MO}  + \overrightarrow {ON} } \right) + \left( {\overrightarrow {PO}  + \overrightarrow {OQ} } \right) + \left( {\overrightarrow {RO}  + \overrightarrow {OS} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {ON}  + \overrightarrow {OQ}  + \overrightarrow {OS}  = \overrightarrow {OM}  + \overrightarrow {OP}  + \overrightarrow {OR} \)

Mà ta có O là trọng tâm của tam giác MPR nên \(\overrightarrow {OM}  + \overrightarrow {OP}  + \overrightarrow {OR}  = \overrightarrow 0 \)

Suy ra \(\overrightarrow {ON}  + \overrightarrow {OQ}  + \overrightarrow {OS}  = \overrightarrow {OM}  + \overrightarrow {OP}  + \overrightarrow {OR}  = \overrightarrow 0 \)

Vậy O vừa trọng tâm của tam giác MPR vừa là trọng tâm của tam giác NQS

Bài 6 trang 97 SBT Toán 10 - Chân trời sáng tạo

Máy bay A bay với vận tốc \(\overrightarrow a \), máy bay B bay cùng hướng có vận tốc chỉ bằng một nửa máy A. Biểu diễn vectơ vận tốc \(\overrightarrow b \) của máy bay B theo vectơ vận tốc \(\overrightarrow a \)của máy bay A.

Lời giải:

Sachbaitap.com